5-1 Middle school math 2원 1차 연립 방정식(two combined linear eqns)에 도전(challenging)하는 TensorFlow 머신 러닝(Machine Learning)
머신러닝의 방법론은 즉 cost 함수를 구성하여 학습에 의해 최종 답을 구하는 과정이다. 하지만 머신 러닝에 의한 거의 대부분의 예제는 선형 회귀 또는 MNIST 문자인식 예제로 도배가 되어 있으며, 그밖에 관심을 가질만한 알기 쉬운 예제가 드물어 보인다. 과연 이 머신 러닝이 뭔가 지능이 있는 인공지능의 일부가 맞기는 한가하는 의심이 들 때가 있다. 그렇다면 사람이 초등학교 때부터 고등하교까지의 교과과정을 통해 체계적인 수학과정을 학습하였다면 수학 문제를 풀 수 있듯이 머신 러닝도 그러한 것이 가능해야 하지 않을까?
그래서 가지게 된 의문중의 하나가 2원 1차 연립 방정식이나 2차 방정식의 해를 과연 머신 러닝의 학습 방법을 통해 구할 수 있는가하는 단순한 의문 제기이다.
여기서는 기존의 선형 회귀 문제나 문자 인식 예제와는 다른 중학교 수준의 수학 문제에 대해서 머신러닝이 어떻게 답을 구할 수 있는지 알아보기로 한다. 이미 거듭 거론 되었지만 머신 러닝에서 문제의 답을 구하는 과정은 우리가 알고 있는 방정식을 푸는 과정과는 판이하게 다르다는 점이다.
중등 수학 수준에서 다루는 2원 1차 연립 방정식 예제는 분명히 4칙 연산을 적용해 방정식을 푸는 과정을 전제로 한다. 이러한 방법론은 컴퓨터를 사용하는 수치해석 방법에 의해 충분히 연립 방정식을 풀 수 있도록 구현되지만 머신 러닝에서는 반드시 적절한 cost 함수 구성이 가능해야하며 학습에 의해서만 답을 구할 수 있는 것이다.
여기에서는 머신 러닝 방식에 의해 2원 1차 연립 방정식을 풀 수 있도록 기하학적인 아이디어로 cost 함수를 구성 하는 방법과 최소제곱법 (least square method)을 적용해 해를 구해보기로 한다.
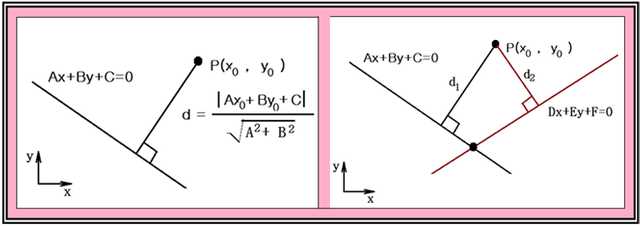
(x,y)평면에서 1차 방정식 Ax+By+C=0 과 평면상의 1점 P (x0, y0) 와의 최소 거리 d는 그림에서처럼 주어진다. 따라서 2원 1차 연립 방정식의 해는 (x,y) 평면상에서 2개의 서로 교차하는 직선의 교점을 구하는 문제가 된다.
그림에서처럼 P점에서 2 직선들과의 수직 거리는 d1과 d2 이며 P 점을 움직여 이 2개의 합이 0 이 되는 위치 좌표가 바로 2 직선의 교점이며 2원 1차 연립 방정식의 해가 된다. 따라서 P점에서 2 직선들과의 수직 거리인 d1과 d2 의 제곱의 합을 cost 함수로 선택하여 그 값을 최소화 하도록 하자.
머신 러닝을 시작하기 위한 초기 조건은 1점 P (x0, y0) 의 값을 TensorFlow 의 난수 명령을 사용하여 임의의 값 즉 (W , b )에서 시작하기로 한다. 여기에서 사용하는 W 와 b 는 선형회귀 분석에서 사용하는 weight W 와 bias b 와는 개념이 다르며 단순하게 W는 x 좌표 x0 이며 b는 y 좌표 y0 로 보면 된다.
주어진 두 직선의 방정식에 대해서 즉 A, B, C, D, E,F 값이 주어진 조건하에서 다음과 같이 cost 함수를 구해보자.
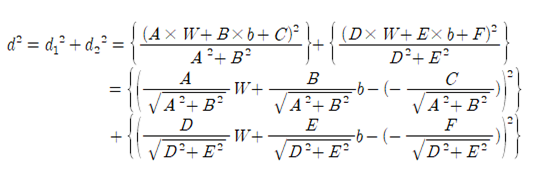
d1과 d2의 제곱의 합이 위와 같이 표현되면 TensorFlow 모듈을 사용하는 linear regression 예제 코드를 간단하게 변경하여 사용할 수 있음을 알 수 있다. 다시 말하자면 선형회귀 분석에서 최소 제곱법을 적용했을 때와 유사하게 W 와 b에 대해서 2차식 형태를 주기 때문이다.
linear regression 예제 코드에서 hypothesis 와 cost 는 다음과 같이 코딩되었음에 착안하자.
hypothesis = x_train * W + b
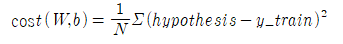
여기서 x_train 과 y_train 은 각각 리스트 데이터 구조를 가진다. 이 코딩을 참조하여 다음과 같이 코드 형태를 수정하자.
hypothesis = A_train * W + B_train * b

여기서 A_train, B_train, C_train 은 다음과 같이 리스트 데이터 구조로 주어진다.
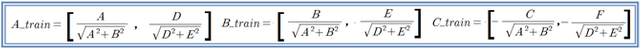
예제 1: A=1, B=1, C=-1 , D=-1, E=1, F=-1인 수치 예제를 다루어 보자. 이 문제는 다음과 같이 2개의 직선의 방정식을 의미한다. 연립하여 풀면 해는 ( 0.0, 1.0) 이 된다.
x + y – 1 = 0,
-x + y – 1 = 0
1/√2 = 0.707 로 두면 리스트 데이터는 다음과 같이 A_train = [ 0.707, -0.707 ], B_train = [ 0.707, 0.707 ], C-train = [ 0.707, 0.707] 로 계산 된다.
코드 실행 결과는 다음과 같다. 주의할 점은 난수 발생이 그대 그때 다르기 때문에 최종 결과는 동일할지라도 수렴하는 과정은 다소 다를 수도 있음에 유의한다. 아울러 learning rate = 0.01 로 설정한다. 만약 여러번 코드를 실행해도 동일한 결과를 얻고 싶다면 코드 실행 때 마다 난수 발생이 항상 동일하게 유지될 수 있도록 TensorFlow에서 tf.set_random_seed(777) 명령을 사용하도록 한다.
라즈베리 파이 보드의 파이선 2.7을 사용해해서 얻은 아래의 결과는 500회 학습 계산에 따른 (W,b) 의 값을 100회 마다 출력해 보았다. cost 함수가 대단히 빠르게 0.0에 수렴하며 2원 1차 연립 방정식의 해 (w, b)가 (0.0, 1.0) dp 수렴함을 확인할 수 있다.
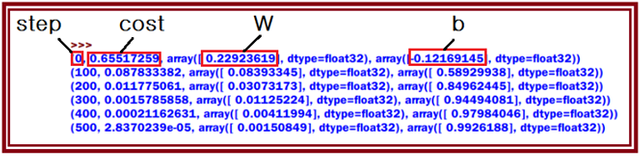
머신 러닝은 방정식의 해를 구하는 문제에 있어서도 우리가 알고 있는 방법으로 푸는 것이 아니라 항상 cost 함수를 구성하여 그 값이 최소화가 되도록 weight 와 b 값을 찾아가는 방법을 사용한다는 점이다.
예제 2: A=2, B=1, C=1 , D=1, E=2, F=-1인 수치 예제를 고려하자. 이 문제는 다음과 같이 2개의 직선의 방정식을 의미한다. 연립하여 풀면 해는 (-1.0, 1.0) 이 된다.
2x + y + 1 = 0,
x + 2y – 1 = 0
1/√5 = 0.447이며, 리스트 데이터는 다음과 같이 A_train = [ 0.894, 0.447 ], B_train = [ 0.447, 0.894 ], C-train = [ -0.447, 0.447] 로 설정 된다.
코드 실행 결과는 다음과 같다. learning rate = 0.05 로 설정한다. 앞서의 코드에서 학습 데이터와 learning rate를 수정하면 충분하다.
600회 학습 계산에 따른 (W,b) 의 값을 100회 마다 출력해 보았다. 최종적인 (W,b)의 값은 (-1.0, 1.0) 임을 알 수 있다.

이와 같이 머신 러닝 기법은 최소제곱법을 적용하여 2원 1차 연립 방정식의 해를 구할 수 있으며 3원 1차 연립 방정식의 경우에도 기하학적인 아이디어를 3차원으로 확장 적용하면 해를 구할 수 있을 것이다.
그렇다면 그 다음 단계로 중학교에서 배우게 되는 2차 방정식을 인공지능의 작은 부분집합에 해당하는 머신 러닝이 학습에 의해 풀어 낼 수 있을 것인가? 과연 풀 수 있다면 어떤 방법으로 hypothesis 와 cost 함수를 설정해야 하는지 차후에 그 길을 제시할 계획이다.
아래 인터넷 주소상의 필자의 블로그에서 연립방정식을 풀기 위한 TensorFlow 파이선 코드예제를 다운 받아 실행시켜 보자. 혹 스팀잇에서 막혀 있어 직접 연결이 안되는 경우 인터넷 브라우저를 따로 열어서 찾으면 된다.