Czym jest i jak działa sztuczny neuron? Jaką drogę musi pokonać sygnał od wejścia do wyjścia i po co nam funkcja aktywująca? Perceptron? A na co to komu? Jaki wpływ na rozwój uczenia maszynowego miał człowiek który wymyślił EKG do badania serca?

Trochę historii:

Do roku 1906 ludzkość nie zdawała sobie sprawy z powszechnie znanego dzisiaj zagadnienia, jakim jest  budowa mózgu. Uważano wtedy, że jest on jednolitą masą, która bierze udział we wszystkich procesach odpowiedzialnych za funkcjonowanie człowieka, nie potrafiono jednak wyjaśnić na jakiej zasadzie mózg - nadrzędny sterownik - miałby nadzorować każdy aspekt naszego życia.

Wszystko zmieniło rewolucyjne odkrycie pewnego hiszpana: Pana Santiago Ramón y Cajal, który wyodrębnił strukturę systemu nerwowego i kształt pojedynczego neuronu, korzystając z dorobku ówczesnych metod fotografii.

źródło grafiki

Świeżo zrewidowane poglądy na sprawę pozwoliły na dalsze odkrycia innych badaczy, i tak np. Pan Einthoven (Taaak, ten sam który wymyślił elektrokardiograf EKG do badania serca) rejestrując biopotencjały tkanek narządów, zajął się również badaniem zjawisk elektrycznych układu nerwowego.

W końcu w swoje ręce oprócz fizjologów temat pochwycili matematycy - ludzie mający tendencję do opisu świata za pomocą modeli matematycznych - i tak w roku 1943 Panowie McCulloch i Pitts biorąc za podstawę sposób funkcjonowania biologicznego neuronu, z pomocą podstawowych operacji matematycznych stworzyli numeryczny opis jego działania, który 14 lat później posłużył innym Panom - Rosenblat’owi i Wightman’owi do budowy (jakżeby inaczej, z przekaźników) pierwszej sztucznej sieci neuronowej - perceptronu - wytrenowanego w celu rozpoznawania liter i cyfr.

Rosenblatt i Wightman, pierwsza sieć neuronowa;   źródło grafiki

I od tego miejsca zaczynamy naszą przygodę.

Przygodo - start

Perceptronem nazywamy sieć zbudowaną z jednego lub wielu sztucznych neuronów umieszczanych kolejno warstwami. W gruncie rzeczy jest on algorytmem - pewną funkcją matematyczną, która przyjmując wiele argumentów (wejść) podaje jedną odpowiedź (wyjście). Pojedynczy neuron sam w sobie jest tzw. klasyfikatorem binarnym - tzn. potrafi on po wcześniejszym treningu odpowiadać (klasyfikować, przyporządkowywać do dwóch możliwych zbiorów odpowiedzi) na przedstawiony mu problem odpowiedzią “tak, jest” lub “nie, nie jest”, lub prościej “prawda” lub “fałsz” czy jeszcze prościej jako “1” lub “0” - stąd binarny, bo jego liczbowa odpowiedź przyjmuje tylko dwie wartości (system dwójkowy operuje wartościami 1 lub 0).

Gdyby bliżej przyjrzeć się w jaki sposób postrzega człowiek, dokonując pewnego uproszczenia moglibyśmy powiedzieć, że w “prawdziwym życiu” jest bardzo podobnie - kierujemy się naszą percepcją - rozpoznajemy że coś jest ciepłe lub nie, że przed nami stoi ściana lub nie, że widzimy znajomą, przyjazną nam twarz życzliwej osoby którą lubimy lub nie - prawda i fałsz, wszystko sprowadza się do algebry Boole’a i logiki matematycznej. Oczywiście mózg człowieka jest bardziej “zaawansowaną” technologią niż jakiekolwiek sztuczne sieci neuronowe skonstruowane do dziś i potrafimy klasyfikować zjawiska spotykane przez nas w codziennym życiu w o wiele szerszy sposób, np. że coś jest super-ciepłe, ciepłe, trochę ciepłe czy w ogóle nie jest ciepłe - nauka znalazła jednak i na to sposób - tzw. logikę rozmytą, gdzie odpowiedzią może być dowolna liczba z przedziału 0 do 1 (np. 0.75 będzie bardziej ciepłe niż zimne, a z kolei 0.5 będzie takie nie za zimne nie za ciepłe). Logika rozmyta jest jednak tematem na inny artykuł. 

Nosacz sundajski o logice rozmytej;  źródło grafiki

Ale o co chodzi..?

Rozważmy budowę biologicznego neuronu i spróbujmy tak jak kiedyś Panowie McCulloch i Pitts “przełożyć” go na opis mogący przysłużyć się inżynierii, czyniąc rozmaite analogie.

Biologiczna komórka nerwowa; źródło grafiki

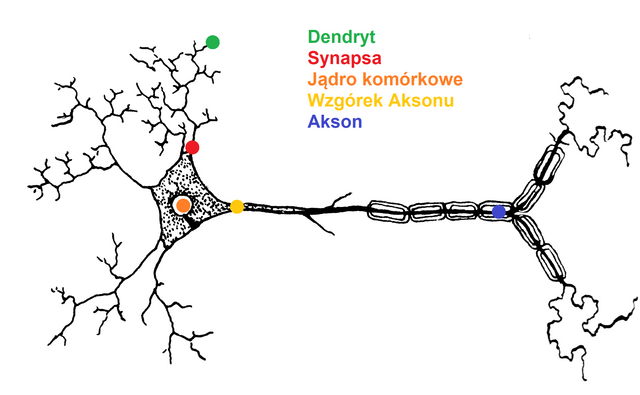
 W budowie neuronu, możemy wyodrębnić:

• dendryty - na które podawane są impulsy (np. elektryczne o odpowiednim natężeniu prądu jak w latach 60-tych lub po prostu wartości liczbowe jeśli zajmujemy się tak wirtualną dziedziną jak programowanie), są one swoistymi wejściami neuronu
• synapsy - które są pewnego rodzaju furtkami i odpowiednio dopasowanymi wzmacniaczami sygnałów które do nich docierają, synapsy posiadają pewną liczbową wagę przez którą będziemy mnożyć wartości podawane z dendrytów. Każdy dendryt posiada odpowiadającą mu synapsę.
• jądro komórkowe - sumujące wszystkie wzmocnione impulsy (wartości liczbowe).
• wzgórek aksonu - działający jako funkcja aktywacyjna (bez aktywacji, to tak jakby odkręcić tubkę z pastą do zębów ale jej nie wycisnąć, a przecież idziemy myć zęby) określająca co pojawi się na wyjściu.
• akson - czyli po prostu wyjście, miejsce gdzie pojawi się odpowiedź którą można wykorzystać w danym momencie lub przekazać dalej do np. kolejnego neuronu

Wiedząc już co nieco na temat poszczególnych elementów pojedynczego neuronu, podzielmy go na bloki oraz stwórzmy jego nowy schemat który od ich nazwy określimy jako schemat blokowy.

Zawiążmy również dżentelmeńską umowę, że przyjmujemy następujący słowniczek do dalszego opisu:

dendryt - wejście x

synapsa - waga w

jądro komórkowe - blok sumacyjny

wzgórek aksonu - blok aktywacji

akson - wyjście y

sygnał - pewna wartość liczbowa, zmienna s

Schemat blokowy neuronu; źródło grafiki: Mistrz Painta

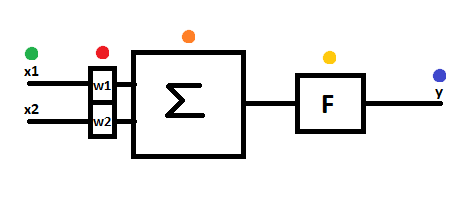
Oczywiście liczba wejść może być nieograniczona - biologiczny neuron posiada tysiące dendrytów - przeanalizujmy jednak prosty przypadek dwu-wejściowego neuronu i tego co będzie się działo z przepływającymi przez niego sygnałami.

1. Na wejścia podajemy sygnały x1 oraz x2
2. Sygnał x1 zostaje przemnożony przez odpowiadającą mu wagę w1, a sygnał x2 zostaje przemnożony przez odpowiadającą mu wagę w2 zachodzi relacja:
s1 = x1w1
oraz
s2 = x2w2
3. Do bloku sumacyjnego docierają sygnały s1 = x1w1 oraz s2 = x2w2, które zostają do siebie dodane zachodzi relacja:
SUMA_SYGNAŁÓW = s1 + s2 = x1w1 + x2w2


a w bardziej formalnym zapisie matematycznym dla przypadku z nieograniczoną liczbą wejść:

SUMA_SYGNAŁÓW =  Σi = 0 xiwi


gdzie:
i - numer wejścia


4. Zsumowany sygnał dociera do bloku aktywacji, gdzie odpowiednia funkcja aktywacji oblicza (klasyfikuje) wynik, który jest podawany na wyjście y
   
   

y = AKTYWACJA(SUMA_SYGNAŁÓW)

Okay, znamy już drogę sygnału i wiemy co się z nim dzieje w trakcie jego przepływu (prosta matematyka). Wypadałoby jednak powiedzieć coś więcej o tej całej funkcji aktywacji. Teoretycznie rzecz biorąc, może być ona dowolna - byleby nam jakoś normalizowała wynik, czyli określała wyjście w pewnej skali która byłaby lepiej czytelna, dobrze byłoby gdyby była też funkcją nieliniową. O ile w przypadku pojedynczego neuronu jest to sprawa typu "doskonale wszystko jedno", o tyle w przypadku całej sieci wprowadzenie nieliniowości ma znaczenie. Najprostszą użyteczną funkcją aktywującą jest funkcja skokowa. Istnieją jej różne odmiany (np. unipolarna lub bipolarna) które działają analogicznie do siebie, rozważymy więc tylko jeden przypadek - funkcję skokową unipolarną.

Jej zasada działania jest trywialnie prosta:

Funkcja skoku;  źródło grafiki

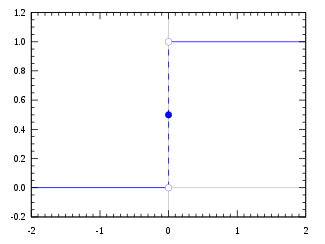
1. jeśli SUMA_SYGNAŁÓW jest większa od 0 to ustaw wyjście jako 1 (prawda) | y = 1 SUMA_SYGNAŁÓW > T = 0
2. jeśli SUMA_SYGNAŁÓW jest mniejsza od 0 to ustaw wyjście jako 0 (fałsz) | y = 0 SUMA_SYGNAŁÓW < T = 0

gdzie:
T  - to próg aktywacji, w naszym przypadku wybraliśmy próg równy 0

Może się zdarzyć, a nawet powinno (w końcu takie mamy oczekiwania), że nasz pojedynczy neuron po wytrenowaniu będzie dokonywał klasyfikacji z zadowalającą skutecznością. Ale czy samojeden neuron może rozwiązać każdy problem jaki przed nim postawimy? Niestety nie - cóż nikt nie jest doskonały.

Pojedynczy neuron nie rozwiąże wszystkich Twoich problemów;  źródło grafiki

Pojedynczy neuron, jest w stanie klasyfikować tylko liniowo separowalne zbiory, czyli takie których reprezentację graficzną dla dwóch zbiorów danych można oddzielić linią prostą. Przypadek dwóch wejść można odwzorować graficznie w układzie Kartezjańskim.

Przykładowa reprezentacja zbioru liniowo separowalnego;   źródło grafiki

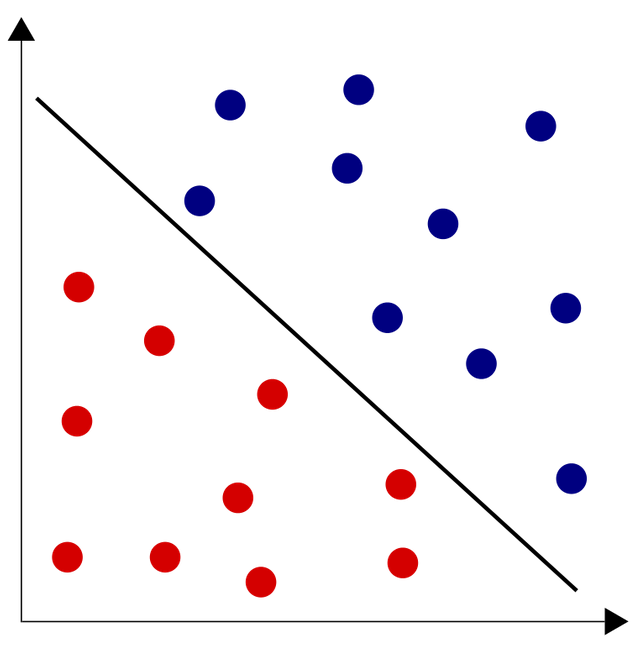
Całe szczęście, pojedyncze neurony można łączyć w bardziej skomplikowane sieci dokonując złożeń i tworząc kilka, a nawet kilkaset ich warstw. Wiedząc o tym i umiejąc to wykorzystać dostajemy do rąk potężne, uniwersalne narzędzie które jest w stanie klasyfikować również liniowo nieseparowalne zbiory i rozwiązywać wieloklasowe problemy jak np. dynamiczna percepcja ruchu w pojazdach autonomicznych.

Przykład wielowarstwowej sieci neuronowej;  źródło grafiki

Moim zdaniem sieci neuronowe to niewątpliwie przydatne i interesujące zagadnienie dla współczesnego świata technologii, który z dnia na dzień pędzi ku jeszcze bardziej świetlanej przyszłości i wygodzie człowieka.

Zakończenie

Co się zaś tyczy bloga, myślę że w najbliższym czasie dodam artykuł poruszający temat trenowania pojedynczego neuronu ponieważ całkowicie pominąłem ten temat, a nie da się przecież mówić o uczeniu maszynowym bez słowa o metodyce treningu. :-) Chciałbym również prosić o komentarz czy obecna forma podawanej treści jest w miarę przystępna - ułatwi mi to nadanie odpowiedniego tonu i charakteru kolejnym artykułom.

Dziękuję za uwagę !

Zobacz również:

Uczenie maszynowe #2 Ten o uczeniu nadzorowanym - regułą DELTA zwanym

Bibliografia

1. R. Tadeusiewicz "Sieci neuronowe" Akademicka Oficyna Wydaw. RM, Warszawa 1993. Seria: Problemy Współczesnej Nauki i Techniki. Informatyka.