<투자 이야기> 투자 수익률의 이해: 두 기간의 평균 수익률과 기하평균

안녕하세요. 오늘도 플랑크톤 스티미언 @mishana입니다.

지난 번 <투자 이야기>에서는 유니클로에 투자하는 방법에 대해서 이야기했습니다.

오늘부터는 수익률 이야기를 몇 편인가에 나눠서 진행해보고자 합니다. 수익률은 투자자라면 반드시 이해하고 있어야하는 내용입니다. 첫 주제로 두 기간의 평균 수익률을 계산하는 방법에 대해서 알아보겠습니다.

단기 수익률 계산하기

철수 씨가 1억을 가지고 2017년 1월 한 달 동안 2,000만원을 벌었다고 가정해보겠습니다. 한 기간의 수익률을 구하려면 최종 자산을 최초의 자산으로 나눠주면 됩니다. 1억 2천만원을 1억으로 나눠주고, 1(원금)을 빼주면 됩니다. 그럼 0.2이 나옵니다. 0.2을 퍼센트로 표시하면 20%가 됩니다.

즉, 철수 씨의 2017년 1월 수익률은 20%가 됩니다. 간단하죠?

철수 씨는 2월에는 3,000만원을 벌었습니다. 이번에도 같은 방식으로 계산을 해보면 25%의 수익률을 기록한 것을 알 수 있습니다.

1월에는 2,000만원의 수익이 났고, 2월에는 3,000만원의 수익이 났습니다. 하지만 수익률로 나눠서 봤을 때는 1월의 수익율은 20%였고, 2월의 수익률은 25%였습니다. 2월의 수익률이 30%가 아닌 이유는 2월초의 원금 크기가 커졌기 때문입니다. 2월을 시작할 때의 원금은 1억이 아니라 1억 2,000만원입니다.

그렇다면 1월과 2월의 수익률 합계를 계산해보겠습니다. 1월과 2월을 하나의 기간으로 생각한다면 최종 자산은 1억 5,000만원이므로 수익률은 50%가 됩니다. 최종 수익률을 계산하는 것은 어렵지 않습니다.

하지만 각 기간의 수익률로 최종 수익률을 알 수는 없을까요? 이미 위에서 이러한 계산을 통해 최종 금액을 계산해보았습니다. 원금에 각 기간의 (1 + 수익률)을 곱해나가면 최종 금액이 나옵니다. 이를 수식으로 나타내면 다음과 같습니다.

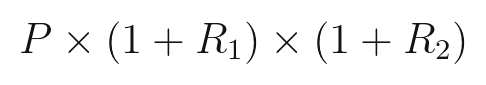
여기서 P는 원금 R₁은 1월의 수익률, R₂는 2월의 수익률이 됩니다. 위의 경우는 다음과 같은 수식으로 작성할 수 있습니다.

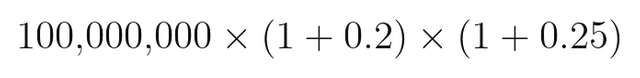
여기서 원금 P를 곱하지 않고, 계산한 값에서 1을 빼주면 최종 수익률만 확인할 수 있습니다.

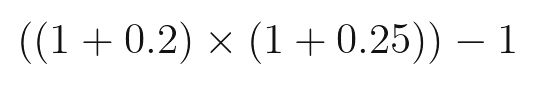
이 식을 계산해 보면 0.5가 나옵니다. 즉 수익률은 50%입니다.

평균 수익률의 함정

그렇다면 1월과 2월의 평균 수익률은 몇 %일까요?

간단하게 생각해보겠습니다. 1월은 20%, 2월은 25%니까 평균을 내볼 수 있을 것 같습니다. (20% + 25%) / 2 = 22.5%가 나옵니다. 월별로 평균적으로 22.5%를 벌었다는 의미가 됩니다.

이 값이 정확한 값인지 간단한 계산을 통해 검증해보겠습니다. 1월에 철수 씨가 22.5%를 벌었다면 자산은 1억 2,250만원이 됩니다. 그리고 2월에 다시 22.5%를 벌었다면, 1억 5006만 2500원 됩니다. 62,500원이 차이가 납니다. 1억 5,000만원과 상당히 비슷하니까 무시해도 될 것 같기도 하지만, 안타깝게도 이 값은 정확하지 않습니다.

이 차이를 무시할 수 없는 이유를 보여드리기 위해, 좀 더 극단적인 예를 들어보겠습니다. 50% 수익이 나고, 30% 손실이 난 경우가 있습니다. 그렇다면 최종적인 금액은 1억 500만원이 됩니다. 평균 수익률은 (50% + (-30%)) / 2 = 10%가 됩니다. 첫 번째 달에 10% 수익이 나면 1억 1000만원이 됩니다. 두 번째 달에도 10% 수익이 나면 1억 2100만원이 됩니다. 무려 1600만원이 차이가 납니다. 사소한 오차가 아니라, 애시당초에 잘못된 계산법이기 때문입니다.

정확한 평균 수익률을 계산하려면 어떻게 해야할까요?

처음에 사용한 평균 수익률을 계산하는 방법을 산술 평균이라고 합니다. 우리가 일상 생활에서 평균을 낼 때 사용하는 방법입니다. 하지만 투자의 세계에서는 산술 평균을 사용하지 않습니다. 바로 기하 평균을 사용합니다.

기하 평균을 사용해 두 기간의 평균 수익률 계산

두 기간의 기하 평균을 계산하는 공식은 다음과 같습니다.

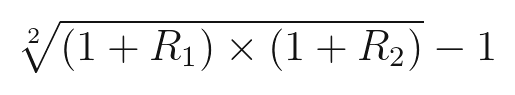
여기서 루트 안의 값은 앞에서 살펴본 수익률을 계산하는 공식이라는 것을 알 수 있습니다. 정확히 표현하면, 수익율에 n루트를 씌워서 평균 수익률을 계산할 수 있습니다. 여기서 n은 기간이 됩니다. 철수 씨의 사례를 대입해보겠습니다. 계산기가 필요합니다.

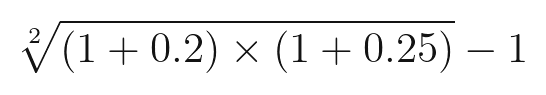
이 값은 대략 0.22474가 나옵니다. 월별로 평균 22.47%의 수익률을 올렸다는 의미입니다. 산술 평균과 상당히 비슷하죠? 하지만 좀 더 정확합니다. 이 방식을 구해진 평균 수익률을 사용해 두 기간 동안의 최종 수익률을 계산해봅니다.

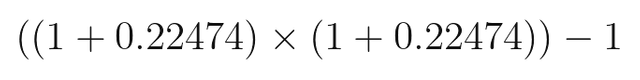
이 값은 대략 1.49999가 나옵니다. 50%에 근접하다는 것을 알 수 있습니다.

앞서 산술 평균으로는 계산이 매우 부정확했던 사례도 살펴보겠습니다. 50% 수익이 나고, 30% 손실이 나는 경우의 기하 평균을 계산해보면 다음과 같습니다.

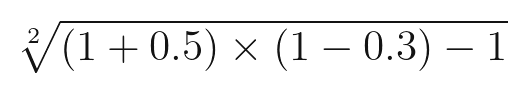
이 값은 대략 0.02469가 나옵니다. 즉 월 평균 2.46%의 수익을 올렸습니다. 산술 평균 10%와는 상당한 차이가 나는 것을 다시 한 번 확인할 수 있습니다. 다시 수익률을 계산하는 공식에 집어넣어서 계산해보면 ((1 + 0.02469) * (1 + 0.02469)) - 1 = 1.04998로 5%에 거의 근접한 값이 나오는 것을 알 수 있습니다. 기하 평균을 사용하니까 두 기간의 평균 수익률이 정확히 계산되는 것을 알 수 있습니다.

투자에서 특정 기간 동안의 평균 수익률을 계산할 때는 기하 평균을 사용한다는 사실을 반드시 기억해두시기 바랍니다. 기하 평균을 사용하기 시작하면 수익률을 둘러싼 다양한 비직관적인 현상들을 목격하게 됩니다. 그 이야기는 수익률 다음 편에서 이어가겠습니다.

---

최근에 공개한 글 목록입니다.

• <책으로 배우는 투자> 존 리, 엄마, 주식 사주세요
• <투자 이야기> 일본 주식 투자: 유니클로에 투자하려면 필요한 최소 금액은?
• <소식> 리디북스, 투자/재태크 서적 무료 대여 이벤트
• <나의 투자> 2018년의 투자 계획: 지속가능한 투자를 향해서
• 2018년 계획의 계획: 글쓰기

---

글쓰고, 프로그래밍하고, 투자하는 @mishana입니다. 트위터 @mishan__a.

• 저는 투자를 권유하지 않습니다. 각자의 선택이고, 결과는 각자의 몫입니다 ;)
• 이 글이 도움이 되셨다면 리스팀, 팔로우 부탁드려요 :)