Rekvijem za Ludwiga Boltzmanna
Prije točno 102 godine, austrijski fizičar Ludwig Eduard Boltzmann oduzeo je svoj život, objesivši se dok je njegova obitelj išla u šetnju. U ovom tekstu se prisjećamo tog genijalca koji je spojio dvije naočigled nespojive stvari: nasumičnost i pravilnosti, te svojom teorijom udario temelje moderne fizike i razumijevanja kompleksnih više-čestičnih sustava.

1. Boltzmann kao fizičar
Ja sam teoretičar od glave do pete. Ideja koja ispunjava moj um i djela je razvoj teorije. Nijedna žrtva nije prevelika za slavu teorije: jer je teorija sadržaj moga čitavoga života.
Nezahvalno je pisati o Boltzmannovim fizičarskim doprinosima u okviru jednog popularnog članka, jer za takvo nešto je zbilja potrebna jedna ozbiljna studija i izrazito debela knjiga. No, možemo izdvojiti ono po čemu je Boltzmann najpoznatiji, a to je po unaprjeđenju (ako ne i formulaciji) statističke mehanike.
Nakon Newtonove mehanike, koja se bavila česticama i pravilima koja prate gibanja i interakciju čestica, razvila se sasvim, naočigled, odvojena disciplina u fizici: termodinamika. Termodinamika je bila zainteresirana za toplinu, energiju i rad.
Prvi koraci prema mostu između te dvije moćne discipline napravljeni su 1859. kada je James Clerk Maxwell formulirao Maxwellovu distribuciju koja je predstavljala distribuciju brzina molekula plina, a koja daje odgovor na pitanje: koje brzine imaju molekule zraka u prostoriji u kojoj se nalazim?
Naravno, nije bilo moguće riješiti Newtonovu jednadžbu za svaku česticu, jer bi tu bila riječ o milijardu milijarda milijarda jednadžbi, što u praksi nije rješivo, stoga se Maxwell poslužio teorijom vjerojatnosti: Maxwellova distribucija pokazuje kolika je vjerojatnost da molekula u prostoriji ima određenu brzinu, pa se iz distribucije mogu izvući podatci i o srednjoj brzini, najvjerojatnijoj brzini, itd.
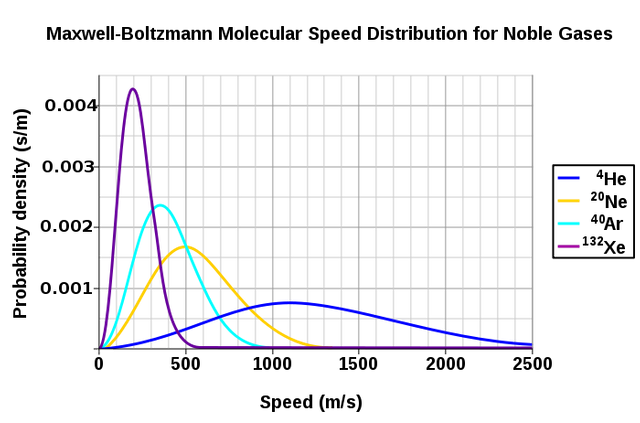
To je bilo originalni pristup problemu jer je u čitavu priču uvedena vjerojatnost, kao poveznica između stroge Newtonove mehanike – koju je u praksi nemoguće primijeniti za opis tako velikih sustava – i termodinamike.
Pet godina nakon toga, Ludwig Boltzmann će se uhvatiti Maxwellove teorije i praktički formulirati statističku mehaniku. Unaprijedio je Maxwellov izračun tako da pokazao da vjerojatnost da čestice imaju određenu energiju ovisi o eksponencijalnom faktoru:
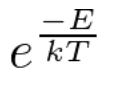
Zatim je uveo fazni prostor, koji je jedna vrsta prostora svih mogućnosti i opisivao je višečestične sustave u tom prostoru, kao i vjerojatnost da se sustav nađe u nekom dijelu tog prostora – te pokazao da ta vjerojatnost mora biti proporcionalna faktoru kojeg je uveo.
.png)
Pa mu ni to nije bilo dovoljno, jer se Maxwelllova distribucija nije mijenjala u vremenu, stoga ga je zanimalo kako se ponašaju ireverzibilni sustavi, u kojima je Maxwellova distribucija tek granični statični slučaj. I to je formulirao, te je u toj formulaciji došao i do zaključka da se sustav giba u "smjeru" u kojem entropija uvijek raste.
1. 0. Iz nasumičnosti prema pravilnosti
Predahnimo malo od ovog formalizma i uočimo što je Boltzmann upravo napravio.
Prvo, krenuo je od pretpostavke da atomi postoje. To je bila hrabra pretpostavka protiv koje je bila većina fizičara i filozofa tog vremena, naročito jer atom nitko nikada do tada nije vidio - a Boltzmann je odlučio napraviti čitavu jednu teoriju baziranu na atomima.
Drugo, teorija vjerojatnosti je temelj Boltzmannovih proračuna. On uzima sustave ogromnog broja atoma/molekula (kao zrak u prostoriji), koje nije moguće - iz praktičkih razloga - riješiti Newtonovom mehanikom, te ih opisiva preko nasumičnih gibanja, sudara, kaotičnosti. No iz te čitave kaotičnosti, on elegantnim matematičkim zahvatima dobiva pravilnosti na makroskopskoj razini.
Posljedično, Boltzmann iz nasumičnosti i vjerojatnosti na mikroskopskoj razini dobiva pravilnosti na makroskopskoj razini; pravilnosti koje možemo koristiti u svakodnevnim proračunima.
1. 1. Problem sa vremenom
Ubrzo su ostali fizičari, dobro naučeni Newtonovom mehanikom, uočili određeni paradoks. U Newtonovoj mehanici ne postoji razlika između toga da vrijeme teče u jednom (+t) ili drugome (-t) smjeru, tj. ako bismo gledali snimku gibanja kuglica na bilijarskoj ploči (+t), a nakon toga gledali snimku u obrnutom smjeru (-t), ne bismo primijetili nikakvu bitnu razliku u ponašanju kuglica. Međutim, u statističkoj mehanici je očito da postoji određen smjer; tako nam je jasno da ako otvorimo bočicu parfema, da će parfem ići u smjeru izlaženja iz bočice (i ispunjavanja čitavoga prostora), te da se neće dogoditi obrnuti proces (da će se molekule parfema početi vraćati u bočicu).

Uočena je "termodinamička strijela vremena" koja se ponaša na način kao da sve oko nas ide prema sve većem neredu. Takva strijela vremena ne postoji u Newtonovoj mehanici. No kako je Boltzmannova teorija sagrađena na Newtonovoj mehanici, uz dodatak vjerojatnosti, postavljeno je pitanje kako je došlo do tog raskoraka.
Boltzmann je i za to imao rješenje. Zbilja se mogu dogoditi oba spomenuta procesa, samo što je prvi proces vjerojatniji, dok je drugi proces enormno malo vjerojatan. U suštini se može dogoditi da se molekule parfema vrate u bočicu parfema, ali je vjerojatnost za takvo nešto toliko mala da se u praksi vjerojatno nikada neće dogoditi. Kao što se u suštini može dogoditi da se sve molekule kisika u našoj sobi nađu u kutu sobe i da zbog toga umremo od gušenja.
Ali zašto je vjerojatniji? Pa zato jer se izlazak parfema iz bočice u prostoriju može realizirati na puno više načina nego što se može realizirati to da se sve molekule parfema, koje su u prostoriji, vrate u bočicu. Točnija, statistička težina W je veća u prvome slučaju, nego u drugome – kao što bi statistička težina da prilikom bacanja dvije kocke padne broj čiji je zbroj veći od 3, bila veća od statističke težne da prilikom bacanja dvije kocke padne upravo kombinacija brojeva 1 i 2. Jednostavno se prvi slučaj može realizirati na puno više načina, nego potonji.
1 . 2. Primjerom prema entropiji
Da bismo dočarali ovo zamislimo da imamo deset osoba koje sjedaju u prvi red i neka svih deset osoba imaju imena koja počinju različitim slovima (npr. Anamaria, Boris, Cetina, David, Filip, Grgo, Hrvoje, Ivana, Karolina, Neven). Pitamo se na koliko se načina mogu realizirati to da se ova grupa od deset ljudi slučajno sjedne u prvi red na takav način da su im imena abecedno poredana (odnosno poredana upravo na ovaj način na koji smo napisali).
Naravno, to je moguće ostvariti na samo jedan način, stoga je statistička težina ovakvog događaja jednaka W=1. W predstavlja broj mikrostanja/načina na koje se neko makrostanje (situacija da su osobe poredane abecedno) može ostvariti. U ovom slučaju dotično makrostanje može se ostvariti na samo jedan način.
Sada se pitamo na koliko je načina (mikrostanja) moguće ostvariti to da se ovih deset osoba poreda na "kaotični" način (makrostanje), odnosno na način da uopće nema reda po početnih slova njihovih imena.
U tom slučaju, odgovor je 10!, odnosno 10x9x8x7x6x5x4x3x2x1 = 3 628 800 načina, stoga je statistička težina W= 3 628 800, te se makrostanje (osobe koje su kaotično poredane) može realizirati na 3 628 800 mikrostanja/načina.
Iz toga možemo zaključiti da je daleko vjerojatnije da se te osobe poredaju bez reda, nego da nasumično formiraju nekakav red.
1. 3. Entropija
Već primjećujemo da se povećanjem statističke težine ujedno povećava i "neuređenost" sustava ("neuređenost" se može realizirati na puno više načina nego "uređenost", stoga je "neuređenost" vjerojatnije stanje). Npr. smatramo da je situacija u kojoj su molekule kisika ravnomjerno rasprostranjene po našoj sobi "neurednija" nego situacija da su sve molekule kisika točno u jednom kutu naše sobe. A upravo je ta "neurednija" situacija puno više vjerojatna od one "urednije" – i sreća da je tako, inače bi se odavno ugušili. Također smatramo da je niz od deset ljudi poredanih abecedno "urednija" situacija od niza od deset ljudi poredanih nasumično, a upravo je potonja situacija puno vjerojatnija.
Boltzmann definira entropiju upravo preko broja mikrostanja s kojima se može ostvariti neko makrostanje:
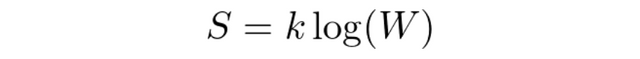
Gdje je k konstantna koja se danas naziva po Boltzmannu. To da će svaki sustav težiti maksimalnoj entropiji, iz ove formule znači da će se realizirati makrostanje koje se realizira sa najvećim brojem mikrostanja (W).
Početna kontradikcija sa klasičnom mehanikom je tek prividna jer će se sustav tipično ponašati na način da se parfem širi iz bočice, a ne vraća u bočicu, ali i dalje će postojati malena vjerojatnost da se dogodi obratan proces.
Ova formula danas stoji na njegovom grobu, kao spomenik jednoj od najdivnijih tajni svemira koje nam je predstavio austrijski fizičar Ludwig Boltzmann.
1. 4. Primjena statističke mehanike
Svugdje.
2. Boltzmann kao filozof
Boltzmann je bio teorijski pluralist. Smatrao je da je teorija tek reprezentacija prirode i da nema neke konačne teorije. Razlikovao je zakone prirode i zakone fizike. Zakoni prirodi su stvarni zakoni po kojima se priroda ponaša, a zakoni fizike su zakoni koje su izmislili ljudi da bi opisali prirodne fenomene; stoga, teorija nije otkriće, nego čovjekov izum. Stoga ne može ni postojati teorija koja bi bila konačna i definitivno istinita, pa čak i kada se čini da je ta teorija obuhvatila sve što se obuhvatiti može.
Bez obzira na matematičku eleganciju Boltzmannove teorije koja je bila u stanju spojiti Newtonovu klasičnu mehaniku sa termodinamikom, odnosno ujediniti te dvije grane fizike u okviru statističke mehanike, skepticizam u znanstvenoj zajednici bio je velik. Naime, vodeći fizičari toga vremena nisu olako prihvaćali hipotezu o postojanju atoma - a Boltzmann je čitavu svoju teoriju razvio iz pretpostavke da atomi postoje. Da problem bude još veći, gotovo svi njemački filozofi tog vremena odbacivali su hipotezu o atomima.
Vodeći protivnik ideje atomizma bio je čuveni austrijski fizičar i filozof Ernst Mach, a među protivnicima tog vremena bio je i Max Planck, koji će kasnije koristiti Boltzmannovu teoriju za neke svoje ključne radove iz kvantne mehanike. Kasnije je Planck, prisjećajući se bitki koje je Boltzmann vodio sa svojim suvremenicima, rekao:
Protiv autoriteta kao što su Ostwald, Helm i Mach, (Boltzmann) nije mogao puno toga učiniti.
Boltzmann je otvorio težak front protiv onoga što je on nazivao "dogmatizam". Naime, filozofi i fizičari tog vremena bili su uvjereni da je Drugi zakon termodinamike, koji opisuje ponašanje entropije, univerzalan i deterministički – odnosno da se ne može prekrišiti. A Boltzmann je upravo svojom formulacijom entropije, pa tako i drugoga zakona, pokazao da se Drugi zakon može prekrišiti (tj. entropija može padati), samo je to izrazito malo vjerojatno da se dogodi. Ali je moguće.
Njegove iscrpjujuće bitke na filozofskom polju trajale su do zadnjeg dana njegova života. Život si je oduzeo 1906., a radovi Einsteina, Smoluchowskoga i Perrina (od 1905. do 1908.) pokazale su da su Boltzmannove ideje bile točne.
3. Boltzmann kao predavač
Boltzman je prema studentima imao izrazito topao i neformalan pristup, što je u ono vrijeme bilo, ne samo rijetko, nego i neobično. Poticao je studente na raspravu i stavljao ih u ravnopravan položaj sa sobom samim.
Stoga nije ni čudo što su njegova predavanja iz fizike i filozofije bila toliko omiljena među studentima, ali i kolegama, da su ljudi stajali na nogama, u prepunim učionicama, i slušali ih. Neki od njegovih studenata bili su i Paul Ehrenfest (kvantni fizičar kojeg ćemo spomenuti kasnije), te Lise Meitner (nuklearna fizičarka čija su otkrića postala standardan dio kurikula nuklearne fizike i čija su otkrića bila vrijedna Nobelove nagrade) koja o Boltzmannovim predavanjima navodi sljedeće:
Držao je predavanje koje je trajalo četiri godine. U to predavanje je spadala: mehanika, hidrodinamika, teorija elastičnosti, elektrodinamika, te molekularna teorija plinova. Napisao bi glavne jednadžbe na glavni dio ploče. Sa strana je imao dvije male ploče na kojima je pisao međukorake. Sve što je napisao bilo je jasno i odlično strukturiranio Imala sam često dojam da je moguće rekonstruirati čitavo predavanje samo sa te ploče. Nakon svakog predavanja imali smo dojam da smo upravo kročili u novi i predivan svijet (fizike), jer je takav bio entuzijazam kojim nas je ispunjavao svojim predavanjima.

4. Boltzmannovi demoni
U statističkoj fizici poznat je Maxwellov demon, gendanken eksperiment u kojem je James Clerk Maxwell 1867. godine pokazao kako bi se, u teoriji, mogao kršiti drugi zakon termodinamike (više o demonu, kao i o simulaciji istoga možete vidjeti na stranicama fizičar Antonia Šibera : http://www.antoniosiber.org/maxwellov_demon_en.html ).
Međutim, Boltzmannovi demoni su bili zloćudnije prirode. Uz zdravstvene probleme kao što su napadi astme, teške migrene, progresivno loš vid, angini, napadi teške depresije, koji bi se danas karakterizirale kao manično-bipolarni poremećaj, bio je Boltzmannov najveći životni uteg. Premda je bio omiljen predavač, vrlo topao prema ljudima, omiljen i na zabavama (bio je poznat po smišljanju šala i izrazito društven), učestalo je padao u teška duševna stanja.
Protiv tih stanja se borio na razne načine, uključujući i česta putovanja/preseljenja. No to nije pomagalo dugoročno, tako je prehavši u Leipzig, već nakon godinu dana pokušao - neuspješno - počiniti samoubojstvo.
Nažalost, njegova bitka je završila u malom mjestu pored Trsta, 5. rujna 1906. godine, u vrijeme kada je već postajalo jasno da je atomarna hipoteza točna.
4. 1. Digresija: Paul Ehrenfest
Njegov student Paul Ehrenfest, kao da je slijedio Boltzmannove stope, unaprijedivši tako statističku mehaniku, točnije kvantnu statističku mehaniku. Ehrenfestov teorem je danas sastavni dio svakog kursa kvantne mehanike. Međutim, i sam Ehernfest je patio od teške depresije, toliko da je Einstein izrazio svoju zabrinutost za njegovu budućnost. Einsteinove slutnje su se pokazale točnim jer je Ehrenfest završio života tako da je ubio sina, a zatim i sebe.
5. Susret sa Beethovenom na Nebu
U vrijeme kada je sve bilo društveno determinirano i u vrijeme kada se vjerovalo u konačne i nepromjenjive zakone prirode, kao i konačne i nepromjenjive društvene zakone u kojima će vladajuća kasta uvijek biti vladajuća, i u kojem se zna tko gdje pripada, Ludwig Boltzmann je razvio teoriju koja se temeljila na nasumičnosti i vjerojatnosti, a koja je, na kraju dana mogla iznjedriti određene pravilnosti. Pravilnosti u kojima zakoni nisu više bili nešto strogo propisano, nego nešto što će se najvjerojatnije desiti, ali uz mogućnost varijacije (premda zanemarivo malene). Kao da to nije bilo dovoljno, Boltzmann čak ni same zakone fizike, koje otkrivamo, nije izjednačavao sa stvarnim zakonima prirode, već sa tek našim pokušajem da te zakone opišemo.
Ludwig Boltzmann je uveo nesigurnost. Elegantnu matematički potkovanu nesigurnost koja je objašnjavala svijet koji vidimo. I zbog toga nas ne treba čuditi što su njegove ideje naletjele na žestok otpor tadašnje filozofske i fizičarske zajednice.
Boltzmann se borio koliko je mogao. I protiv svojih kolega i protiv svojih unutarnjih demona. Patnja se protezala kroz njegov život, ali i borba protiv iste u vidu toplih odnosa prema ljudima, susretljivosti i društvenosti.
Na jednoj od zabava, koje je rado i posjećivao i priređivao, Boltzmann je, u zadnjim godinama svoga života, napisao pjesmu posvećenu Beethovenu: Beethoven im Himmel . Beethovenu, čije su ga skladbe dugo vremena vadile iz teških duševnih stanja i uljepšavale mu život.
U toj pjesmi on na Nebu susreće velikoga Beethovena i sluša njegove skladbe. No, umjesto veličanstvenosti melodije na koju je navikao, na Nebu čuje Beethovena u sasvim drugom stanju: stanju monotonih i dosadnih tonova koje proizvodi slavni majstor.
Anđeli Boltzmannu objašnjavaju da im na Nebu nedostaje patnja.
Patnja, koja je fundamentalni sastojak njegovog stvaralaštva.
++++++++++++++++++++++++++++++++++++++++++++++
Beethoven in Heaven
Done with dying and deeds unsung
My soul found solace on a higher rung.
Soaring, swooping, serenely swift
I caught a draft, an upward drift,
And there beyond Earth's spinning madness
I found God's world of winning gladness.
Glued to enter what most inspires
I heard instead his glorious choirs,
And angels fair sang songs so sweet
In words of joy none can repeat.
But still a flaw my ears did find:
Monotonous tone to bore the mind.
A gentle angel laughed to allay:
'Thou must be German of musical clay.
We envy thy skill in song and sound,
But God is eternal, forever bound.
The muse of time doth never end
And the tone of goodness can never bend. '
But voices vaunt a grand chorale
Of vintage Beethoven theatrical.
But clear and true, its completely new,
A work unnamed and below unfamed.
On God's command he wrote and planned;
The notes took shape appropriate, but bland.
++++++++++++++++++++++++++++++++++++++++++++++
REFERENCE
Ludwig Boltzmann His Later Life and Philosophy, 1900–1906 Book One: A Documentary History Editors: Blackmore, J.T. (Ed.).
Great Physicists: The Life and Times of Leading Physicists from Galileo to Hawking Paperback – September 16, 2004 by William H. Cropper, Ch. 13.
Marcelo B. Ribeiro, Antonio A. P. Videira, Boltzmann's Concept of Reality: arXiv:physics/0701308
Cercignani, C. (1998). Ludwig Boltzmann. The man who trusted atoms. With a foreword by Roger Penrose. Oxford: Oxford University Press.
https://en.wikipedia.org/wiki/Ludwig_Boltzmann
Slike su povučene sa stranica koje dozvoljavaju slobodno korištenje slika.
Hej, dobrodošao nazad! Ja mislio ti odustao posle dva-tri sjajna posta :)
Ma ne, samo.. život i obaveze :D Sad sam malo prepravio post jer sam vidio da su neke stvari nejasne. Netko mi je preporučio da "izbacim fiziku i da će post biti puno bolji", što me sjetilo onoga što je Hawking rekao kada je pisao svoju prvu knjigu: da je pazio da nema jednadžbi u knjizi jer svaka jednadžba prepolovi broj čitatelja (stoga je žrtvovao pola čitatelja radi E=mc2) :)
Congratulations @everett57! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Ovo je, nažalost, ostalo retko i neobično do danas. Sjajan tekst, uživao sam čitajući.
Hvala na feedbacku. Čak su mu takav pristup ostale kolege (uključujući i Macha) otvoreno zamjerale, jer nije bio dovoljno "formalan" i "ozbiljan", što s eočekivalo.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @everett57!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations @everett57! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @everett57! You received a personal award!
Click here to view your Board
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness and get one more award and increased upvotes!
Congratulations @everett57! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!