Source: https://i0.wp.com/amyxinternetofthings.com/wp-content/uploads/2017/08/Quantum-Cryptography-2.jpg

At this moment, I will share my project about one of the most popular cryptography algorithms, i.e. Advanced Encryption Standard. If you have a strong passion in the study of cryptography, feel free to read my article.

Murez Nasution

Attention!
You need have several common studies of basic mathematics in Cryptography to completely understand this article.

Preface

Advanced Encryption Standard (AES) also known as Rijndael, is an encryption algorithm used as a Federal Information Processing Standards (FIPS) standard by The National Institute of Standards and Technology (NIST) in 2001. AES is intended to gradually replace DES (Data Encryption Standard) as an encryption standard in the United States for the 21st century (DES as FIPS standard has been revoked, May 2005). AES becomes standard through the selection process. Of the several encryption algorithms nominated to be AES, the selected one is Rijndael encryption. Thus, the AES algorithm is also known as the Rijndael algorithm. This encryption technique includes block cipher type as well as DES. The main difference between DES and AES encryption is in the subBytes transformation (using S-boxes). AES performs a direct transformation of the message, while DES uses S-box substitution only in the cipher f function, whose results are then operated against the message using exclusive OR. AES also uses a larger encryption keys, such as 128 bits, 192 bits or 256 bits (Kromodimoeljo, 2010).

In general, the transformations in the Rijndael algorithm consist of: subBytes, shiftRows, mixColumns, and addRoundKey. The Rijndael algorithm operates on the state of the message as a 4 × N_b matrix. Each column of state represents 1 word, with s_{0, i} as the most significant byte for the i-th column. Some operations on the Rijndael algorithm are defined at the level of bytes that represent members in the polynomial field GF(2⁸). Other operations are defined in terms of 4-byte word (Daemen & Rijmen, 2002).

Encryption

---

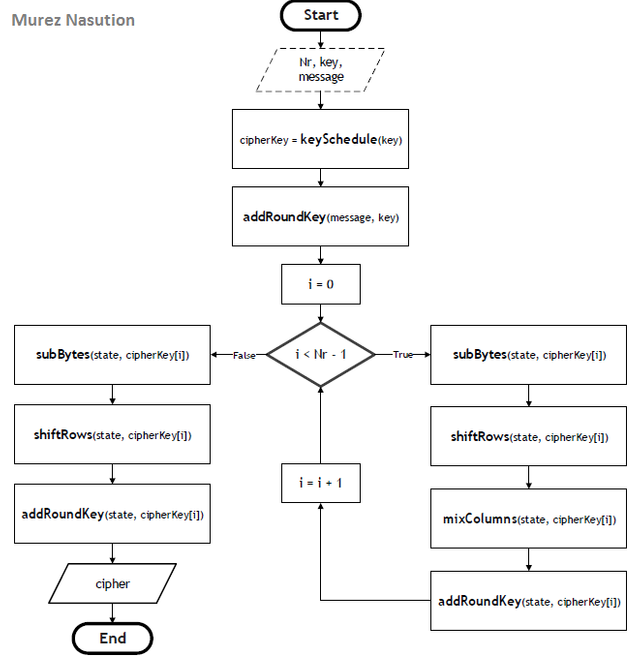
The AES encryption process performs subBytes, shiftRows, mixColumns, and addRoundKey repeatedly transforms up to N_r- 1. While cursor at the N_r, the transformation is still the same, but without the mixColumns transformation. Here pseudo-code of AES encryption:

Round(state, roundKey)
1. subBytes(state);
2. shiftRows(state);
3. mixColumns(state);
4. addRoundKey(state, roundKey);

Transformation of subBytes

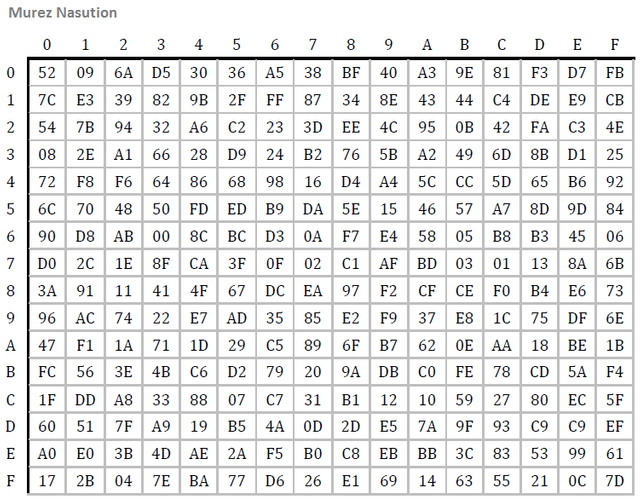
The subBytes transform is a non-linear byte substitution, which operates on each byte on the state independently. The substitution table (S-box) can be reversed (inverse) and made with two transformations. First, using multiplication inverse in GF(2⁸), then apply affine transformation in GF(2⁸) (Daemen & Rijmen, 2002) defined as follows:

---

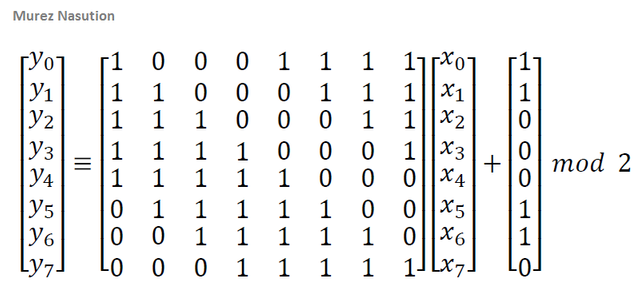
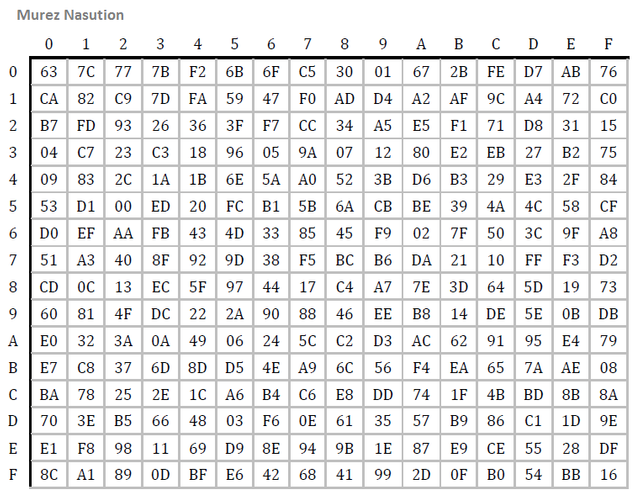
Table of AES S-Box.

Example:
subBytes(A7) = 5C
subBytes(3F) = 75.

Transformation of shiftRows

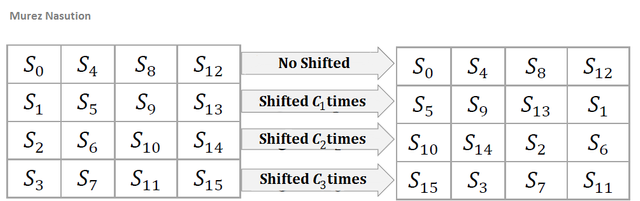
In the shiftRows transformation, the row of states is shifted (left) as much as n times. For N_b< 8, the first row does not move, the second row is shifted once to the left, the third row is shifted twice to the left, and the fourth row is shifted three times to the left or shifted once to the right. This shift is denoted by C₁, C₂ and C₃ depending on the length of block N_b (Daemen & Rijmen, 2002) as in below:

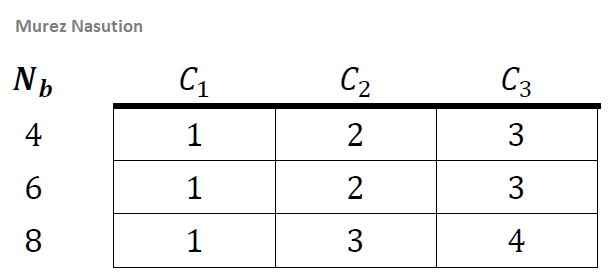
Illustration:

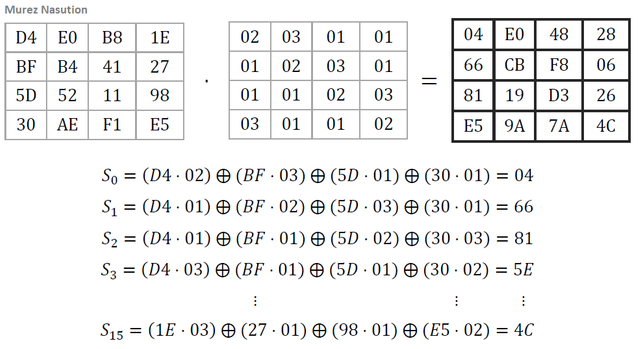
Transformation of mixColumns

In the mixColumns transformation, each column in the state can be viewed as a polynomial in GF(2⁸) and multiplied by a fixed polynomial modulo x⁴+ 1, i.e. c(x) = 03x³+ 01x²+ 01x + 02. This polynomial is relatively prime for x⁴+ 1 and has an inverse (Daemen & Rijmen, 2002). Let b(x) = c (x) ⨂ a (x), then the matrix multiplication is:

Example:

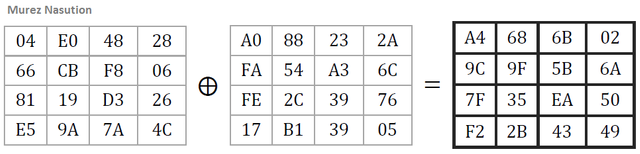
Transformation of addRoundKey

This transformation is quite simple, i.e. by performing XOR operation against cipher key with state. Cipher key is obtained through key schedule process, some call this process with key expansion. The length of the cipher key varies depending on the key length (Daemen & Rijmen, 2002).

For 128-bit AES with state of 4 words, a cipher key of 44 words is required. This is because the number of loop is 10 times, with each round required N_k of 4 words to be XOR to the state with the same magnitude (N_b = 4 word). Thus, the total length of key is 4 * 10 word = 40 word plus the first addRoundKey, so 40 word + 4 word = 44 word. The same for 192-bit and 256-bit AES, the required lengths of cipher key are 52 words and 60 words respectively.

The length of state N_b must be equal to the length of the N_k key, as follows:

Summary of AES Encryption

Decryption

---

The AES decryption algorithm is the inverse of the AES encryption algorithm, in which the number of rounds remains the same, but in the first round of transformation is addRoundKey, shiftRows and subBytes. The rest of the next round is transformed in the following order: addRoundKey, mixColumns, shiftRows, and subBytes.

Transformation of subBytes Invers

Just like the encryption, it's just the inverse subBytes transformation in the decryption using the inverse S-box table obtained from the inverse of the affine mapping, followed by inverse multiplying in GF(2⁸), as seen below:

Transformation of shiftRows Invers

In decryption, inverse shiftRows are transformed in the opposite direction to shiftRows on the encryption. So, in this context, the direction is to the right.

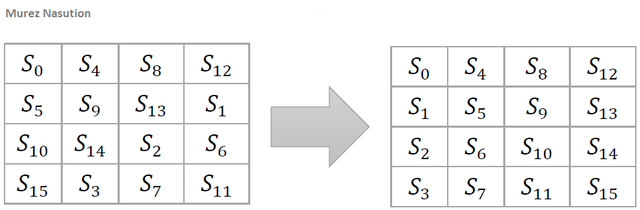
Transformation of mixColumns Invers

The inverse mixColumns transformation is the same as in the encryption, it's just that every state column is transformed by multiplication to polynomial of 0Bx³+ 0Dx²+ 09x + 0E. Which meets the inverse law:
(03x³+ 01x²+ 01x + 02) ⨂ (0Bx³+ 0Dx²+ 09x + 0E) = 01,
so the matrix multiplication is:

Summary of AES Decryption

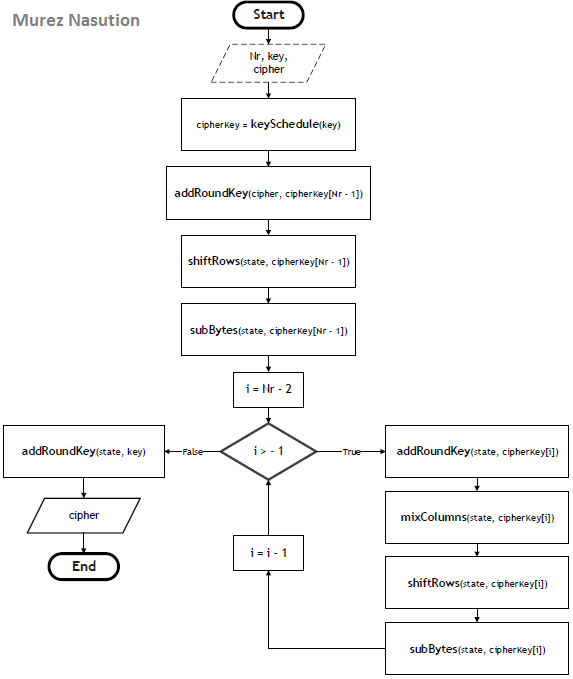
Key Schedule

---

Round key comes from the cipher key by using the Key schedule process which will be required in the addRoundKey transformation, where XOR process is performed on the state with round key. This process consists of two steps, namely key expansion and round key selection. The basic principle is as follows:

• The number of round keys in bits is equal to the length of block multiplied by the number of rounds plus one. (For example, for a block length of 128 bits and 10 rounds, the required number of round keys is 1408 bits).
• Round key is taken from the expanded key (the cipher key that has been advanced) in the following way: the first round key is taken from the first N_b word, the second round key is taken from the next N_b word, and so on.

The expanded key is an array of 4-byte word and denoted by W[N_b* (N_r+ 1)]. The first N_k word contains the cipher key, while the other word is recursively defined in the word with smaller index. The key expansion function depends on the value of N_k.

As of now, subByte(W) is a function that returns a 4-byte word, where each byte is the result of applying a Rijndael S-box to a byte whose position corresponds to the input of word. The rotByte(W) function returns a word in which an input of word(a, b, c, d) produces the word (b, c, d, a).

At first N_k is filled with cipher key. Each next word W[i] is the same as XOR with the previous word W[i-1] and N_k word is positioned with W [i - N_k]. For word in position which is a multiple of N_k, the transformation by XOR operation is applied first to W[i - 1] with and the constant rotation.

This rotation constant is defined by: Rcon[i] = [ RC[i] 00 00 00 ], in which RC[i] represents the element in GF(2⁸) with the value of x^{(i - 1)}. The i-th Round key is the same as word W [N^b* i] to W [N^b* (i + 1)].

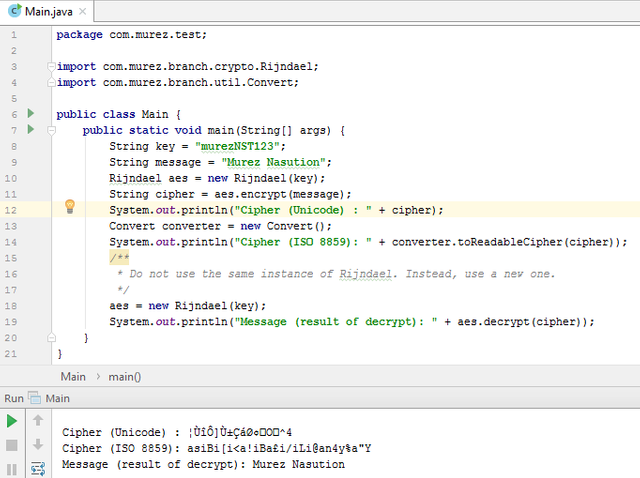
The Result of Implementation

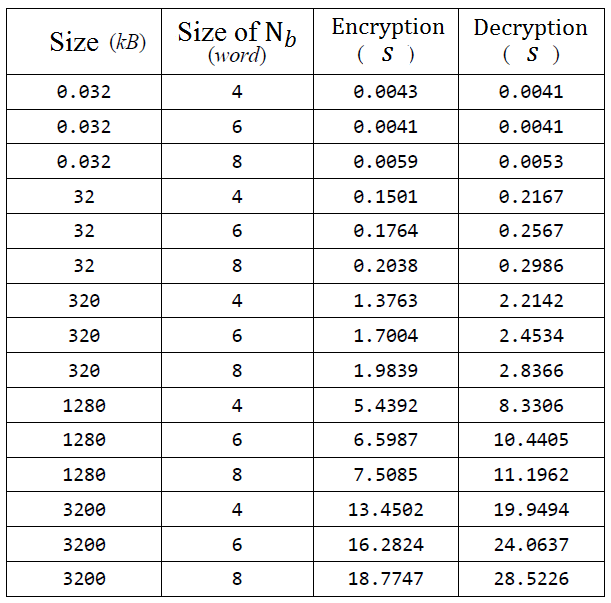
Rijndael algorithm speed of encryption / decryption test results

---

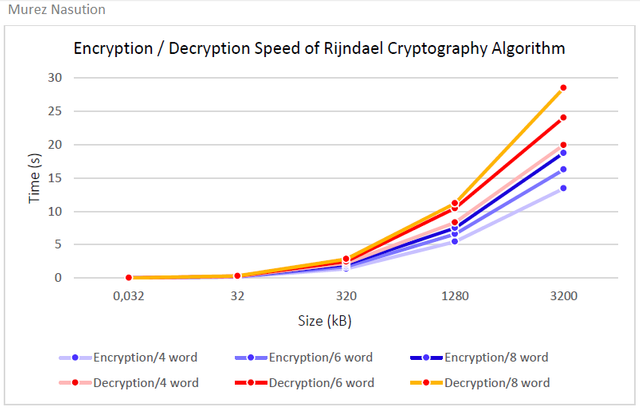
Summary

---

1. Encryption on Rijndael cryptography systems is faster than the its decryption.
2. The N_b block that are getting larger when encrypted will require a longer processing time.

---

Posted on Utopian.io - Rewarding Open Source Contributors

---