미국 장기 금리 예측 시계열 분석 1

안녕하세요~!
오늘은 시계열 분석을 해보도록 하겠습니다.
오늘은 미국의 장기 금리 데이터를 이용하여 시계열 ARIMA 모형에 적합해보고,
예측해보는 것까지 하도록 하겠습니다.
사실 목표는 시계열회귀분석까지 해보는 것인데요. 이번 포스팅에서는 못할 것 같습니다.
데이터는 2013년 1월 1일부터, 2022년 4월 6일까지 일별 데이터입니다.
아쉽게도 2008년 데이터는 없네요..
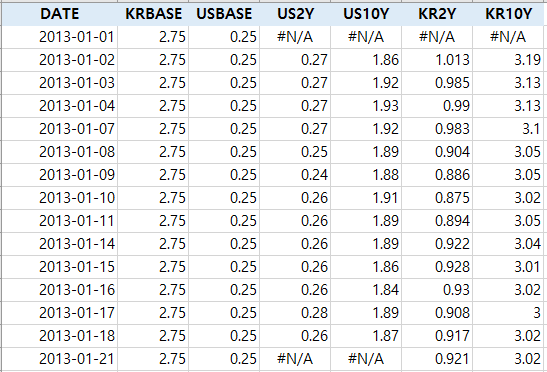
아래는 변수에 대한 간략한 설명입니다.
(오늘 볼 시계열은 US10Y에 국한되어 있긴 합니다)
KRBASE: 한국 기준금리
USBASE: 미국 기준금리
US2Y: 미국 2년채금리
US10Y: 미국 10년채금리
KR2Y: 한국 2년채금리 (14년도부터 산출이 중단되었죠)
KR10Y: 미국 10년채금리
분석 툴은 R이고, 불러와서 간단한 전처리를 해주었습니다.
저는 데이터 분석을 할 때는 주로 R을 사용합니다.
딥러닝을 할 때는 Python을 주로 이용하구요.
오늘은 간단한 시계열 분석을 해볼 것이기 때문에 R을 이용해보겠습니다.
R에서 쓸 패키지를 먼저 불러와주시구요. 엑셀도 함께 불러와줍니다.
'
packages <- c("tidyverse","foreach","readxl","stringr",
'imputeTS', 'TSstudio','forecast','dynlm', 'lmtest',
'sandwich','ggeffects', 'xts')
sapply(packages,require,character.only=TRUE)
rm(list = ls())
IR <- read_excel('장기금리예측.xlsx',sheet = '금리')
'
오늘은 미국 국채 10년물과 2년물에 대해 볼건데요,
위에 엑셀 파일에서 보듯이 결측값들이 있습니다.
결측값을 잘 채우는 것도 데이터 핸들링의 아주 큰 분야입니다.
전체의 평균으로 채워넣던, 전체 중앙값으로 채워넣던..
데이터를 다루는 사람의 철학이 들어가는 분야이니까요.
시계열, 특히 2년물 10년물 금리 데이터에서 저는 바로 이전 known value 값 그대로 사용하는 것을 택했습니다. 이유는, 정상시계열이면 그래서는 안되지만, 어제의 금리는 오늘의 금리와 사실 무관하지 않다는 판단 하에서입니다. 정상 시계열은 아래에서 설명 하도록 하겠습니다.
결측값을 채워넣고, 시도표를 그려보도록 하겠습니다.
'''{r}
IR$US10Y <- c(IR$US10Y[2],na.locf(IR$US10Y))
IR$US2Y <- c(IR$US2Y[2],na.locf(IR$US2Y))
R 최신버전(4.1.3) 이슈로 XTS는 column마다 적용해줘야 함..
US10Y <-xts(IR$US10Y, order.by=as.POSIXct(IR$DATE))
US2Y <-xts(IR$US2Y, order.by=as.POSIXct(IR$DATE))
plot.xts(US10Y)
'''
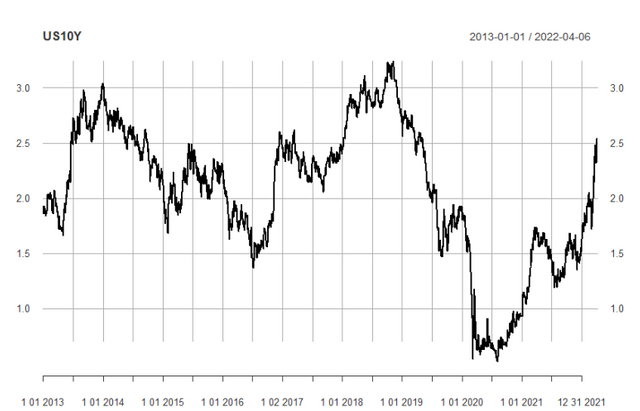
시계열 분석을 하려면, '정상시계열'이라는 개념을 알아야 합니다.
우선 시계열을 확률과정(stochastic process)으로 보았을 때,
평균이 일정하고
분산이 존재하며 상수이다.
두 시점 사이의 자기공분산은 시차에만 의존
위 세 가지를 만족하는 시계열을 '정상시계열'이라고 하는데요,
정상성을 만족하지 못하는 시계열은 시계열 모형 ARIMA를 사용할 수 없습니다.
그래서 만약 위 3가지 만족을 하지 못한다면, '변환'을 해서 시계열의 형태를 바꾸어줄 필요가 있습니다.
많은 경제 시계열의 경우, 추세가 증가함에 따라 계열의 변동도 함께 커지는 것이 사실인데요,
미국 국채 10년물도 보시면 제 육안 판단으로는 평균도 일정하지 않고(추세가 보이고),
분산도 시간이 지남에 따라 커지고 있는 것 같습니다.
그래서 저희는 정상 시계열을 만들어 줄 것입니다.
- 분산 안정화
분산안정화를 위해서는 멱변환(power transformation)이 필요합니다.
가장 대표적인 예로, 로그변환인 것이죠.
실제로 경제변수를 다루는 시계열에서는 로그변환이 분산 안정화를 잘 잡는다는 논문도 있습니다.
(많은 사회과학 데이터는 exponential 형태이기 때문이죠)
주의할 점은, 분산안정화, 차분을 둘 다 이용할 경우, 분산안정화 과정을 차분보다 먼저 해주어야 한다는 것입니다. 차분 부터 수행할 경우 데이터에 음수가 나올 수 있어, 차분 뒤 로그변환을 해줄 경우 -INF가 나올 수 있기 때문입니다.
분산 안정화는 Box&Cox(1964)가 소개한 정규화변환을 이용하도록 하겠습니다.
'''{r}
#분산안정화
lambda <- BoxCox.lambda(IR$US10Y)
lambda
'''
결과, lambda 값이 1.32가 나왔습니다.
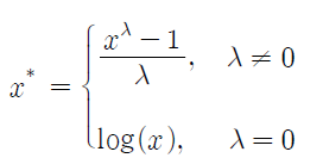
x*는 변환된 자료를 의미하고, 위 코드의 결과로 lambda 값이 나오게 됩니다.
아래 표에서는 lambda 값별, 변환방법을 소개하고 있습니다.
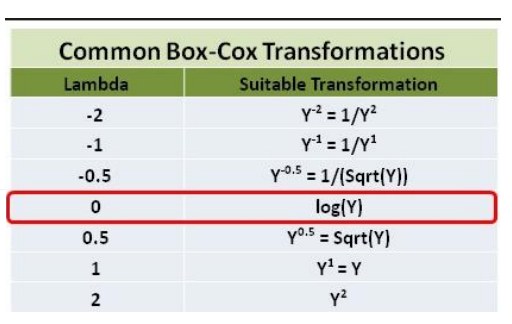
lambda값이 1이라 함은, 분산이 제 생각보다는 시간이 지남에도 변동성이 비슷하다는 말입니다.
1.32가 나왔는데요, 제 주관적 의견으로는 lambda 값이 1.32면 분산이 시간이 지남에 따라 일정하다고 판단하고 데이터의 아무런 가공 없이 모형을 적합시켜도 된다고 생각합니다.
그러나 이번 포스팅에서는 cox 변환을 해보도록 하겠습니다.
'''{r}
US10Y_cox <- BoxCox(US10Y, lambda)
'''
- 추세 없애기
그 다음, 추세를 없애주도록 하겠습니다.
추세가 있으면, 모형을 적합시켰을 때 잔차의 자기상관이 높게 되어 쓸 수 없는 모형이 나옵니다.
추세는 보통 차분을 이용하여 제거해줍니다.
'''{r}
coxdiff_US10Y <- base::diff(US10Y_cox, lag = 1, differences = 1)
plot.xts(coxdiff_US10Y)
'''
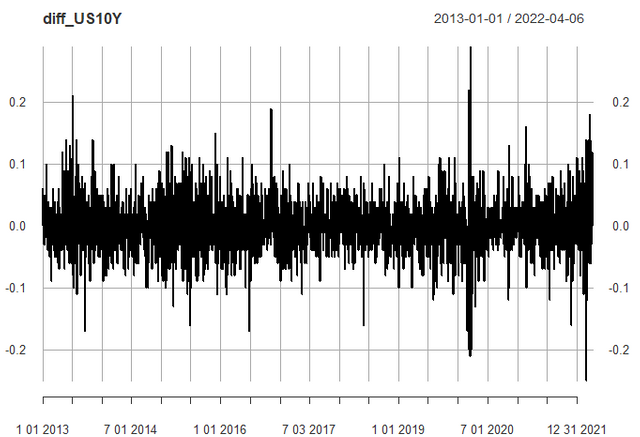
1차 차분 한 번 해주었을 뿐인데, 추세가 없어진 것이 보이시죠?
시계열 분석을 하려면 추세를 제거해주는 과정이 꼭 필요합니다.
그 다음에는 모형을 적합하고, 진단하고, 예측을 하는 단계가 남았는데요.
쓰다보니 포스팅이 길어져서 제 2편으로 돌아오도록 하겠습니다.
2편도 기대해주세요!
도움이 되었다면 upvote 부탁드립니다! ( ღ'ᴗ'ღ )
안녕하세요 스팀잇 세계에 오신것을 환영합니다.
저는 여러분이 스팀잇에 잘 적응 할 수 있도록 응원하고 있습니다.
이 포스팅을 한번 끝까지 읽어보시고 STEEMIT-초보자를위한 가이드
혹시나 궁금하신 내용이 있으면 언제든
@ayogom, @jungjunghoon, @powerego, @tworld, @dorian-lee, @bitai, @kinghyunn, @maikuraki, @hiyosbi, @nasoe, @angma, @raah 님께 댓글 주시면 친절하게 알려드리겠습니다.
카카오톡 방에서 궁금한 점도 한번 해결해 보세요. 많은 스팀잇 경험자 분들께서 언제나 궁금한 부분을 즉시 해결해 주실 것입니다. 카카오톡 대화방 바로가기 패스워드(1004)