Variable-Length Floating Point Numbers
I've been working on a project recently, and one thing it uses is variable-length numbers. There are several resources for variable-length integers, but, while it may exist somewhere on the internet, I haven't found anything on variable-length floating point numbers. Here's a way to do that. But first let's cover variable length integers.
Variable-Length Integers
Variable-length Integers encode a given number into one or more bytes of data. The number of bytes required for a number varies depending on the number. Among the many ways of doing this, I've been using a variation on Little Endian Base 128 (LEB128) format.
To encode, a number is split into 7-bit segments, all but the most significant 7-bit segment that is not all zeros get tagged with a 1 bit, then the 8-bit segments are written to storage. In my case, I've made a minor variation in that if the number would require that all 64 bits of the number to be provided, the last byte is a full 8-bits with an implicit stop. This way, a 64-bit number takes only 9 bytes instead of 10 (7 bits x 8 + 8 bits = 64 bits, +8 bits of flags).
One additional variation that I haven't implemented yet is a technique used by git for their variable-length quantities (VLQ) which offsets each number encoded so that there is only a single representation of a given number. Without this, the byte sequences 0x00, 0x80 0x00, 0x80 0x80 0x00, and so on all encode the number zero (0). With this modification, the largest single-byte code (0x7F) encodes the number 127, and the smallest 2 byte code (0x80 0x00) encodes the number 128. The effect is that there is now 128 numbers that before would have been 3-byte codes that are now 2-byte codes, and this effect repeats at each additional byte boundary.
Floating Point Numbers
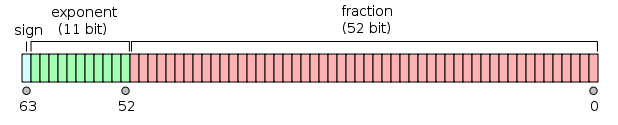
IEEE 754 Double Precision Number Image Source
Floating point numbers have a different layout than integers. For integers, the number 1 is stored in memory as the 64-bit number 0x0000000000000001, while the floating point number is stored in memory as 0x3FF0000000000000. If passed into the LEB128 encode function, the floating point number will take 9 bytes (0x80 0x80 0x80 0x80 0x80 0x80 0x80 0xF8), while the integer takes only 1 byte (0x01). The problem is that the bits set with the floating point format are near the most-significant bits, while for the integer, they are at the least-significant bits.
The way to get around this problem is by mapping the floating point number to another number that will encode with fewer bytes without losing any information. First the exponent, which is in the IEEE 754 floating point format is stored as an offset value, meaning that 2^0 is represented as the number 111 1111111 (0x3FF, 1023), is changed to a sign+magnitude format, with zero being +,00 00000000, -1 being -,00 00000000. Then the sign, modified exponent, and mantissa are shuffled. Here's what I have in mind:

The sign, exponent sign, and the most significant three bits of the mantissa and least significant two bits of the modified exponent go into the first byte of output. If everything else is zeros, then the encoding stops. Then, as needed, the next 4 bytes have 2 bits of exponent and 5 bits of mantissa. The next 3 bytes have 7 bits of mantissa, and the last byte the least significant 8 bits of the mantissa.
Now, this works great if the number happens to have zeros low in the mantissa or high in the exponent, but what if the mantissa is entirely used up. This is more common that you may think, with common numbers like 1/3 having a repeating 010101 for the entire mantissa (0x3FD5555555555555). If you have only the number, there is no way to infer that bits can be dropped, but when parsing code, there is more information available, namely the number of significant figures the programmer uses when writing the number. The number 3.0 needs fewer bits than 3.00001 will.
I haven't coded this up yet, so I don't have any information on how efficient this is in practice, but I expect this will work with at most minor changes. Once I do have usage information, I'll probably have another post on it.
Hello! Your post has been resteemed and upvoted by @ilovecoding because we love coding! Keep up good work! Consider upvoting this comment to support the @ilovecoding and increase your future rewards! ^_^ Steem On!

Reply !stop to disable the comment. Thanks!