Almost every new technology that lets you wonder how do they know that or how do they do this deploy deep learning algorithms — the secret sauce of artificial intelligence.

Among many other things, here is a short and sweet list of some impressive tasks that deep learning accomplishes or contributes to.

• translate between languages
• recognise emotions in speech and faces
• drive
• speak
• spot cancer in tissue slides better than human epidemiologists
• sort cucumbers
• predict social unrest 5 days before it happens (highly interesting; read more about it here)
• trade stocks
• predict outcomes of cases of European Court of Human Rights with ~80% accuracy (read)
• beat 75% of Americans in visual intelligence tests (read)
• beat the best human players in pretty much every game
• paint a pretty good van Gogh (read)
• play soccer badly (read)
• write its own machine learning software (read)

As artificial intelligence is already very advanced, it is still in the beginning and thus an understandable technology that is not too late to learn yet.

If you would like to have a basic understanding of how deep learning works in general, I recommend you to read this blog post series. This post is the third piece of it.

To read the first introductory part, click here.
To read the second part, click here.

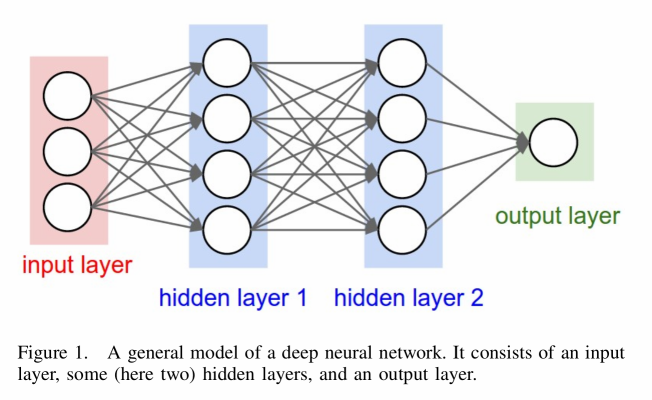
Here we explain how a convolutional neural network is built. They are used when objects need to be identified within images. To keep the big picture, we repeat some parts of the second blog post.

Generally — Deep learning (DL) is a field of artificial intelligence (AI) that uses several processing steps, aka layers, to learn and subsequently recognize patterns in data. These methods have dramatically improved the state of the art in speech recognition, visual object recognition, and many other domains.

3. Deep Learning Convolutional Neural Networks

DL architectures that are called convolutional neural networks (CNNs) are especially interesting because they have brought about breakthroughs in processing video and images. And, in the same time, they are relatively straight forward to understand. Their quick off-the-shelf use has been enabled by open source libraries such as TensorFlow or theano.

The founding father of CNNs is Yann LeCun who published them first in 1989, but he had been working with them since 1982. Like every deep neural network, CNNs consist of multiple different layers — the processing steps.

The speciality here is the convolutional layer in which the processing units within a layer work in such a way that they respond to overlapping regions in the visual field. In simple terms, since a convolutional layer processes let's say an image parallelly, it works in an overlapping manner to understand the full image properly.

The processing units are also known as neurons to further nurture the analogy to a human brain.

To understand the big picture of a DL architecture, I will not only explain how a convolutional layer works, but also the input layer, a rectifier linear unit layer (relu), a pooling layer, and the output layer.

Later in the blog post series, I go beyond theory and build a CNN using the open source software TensorFlow to run the CIFAR-10 benchmark. It consists of 60k images and requires them to be classified correctly at the end.

Some examples how the CIFAR-10 dataset looks like:

We will see later how the deep learning network learns by using a simple method called gradient descent. In AI it is possible to measure how well or bad a network learned and we as well will see how the loss per every learned bit gradually decreases. The loss tells us how wrong the network currently is.

A. Input Layer

The nodes of the input layer are passive, meaning they do not modify the data. They receive a single value on their input, and duplicate the value to their multiple outputs which are the inputs of the following layer.

To better describe what values the input layer propagates, let's take a closer look at an image input. For example, if we take an image of a black four on white background, then one possible way to interpret its values could be that the processing units translate the input values into values from −1 to +1. While white pixels are then denoted by −1, black pixels would denote +1 and all other values, like transitions between black and white regions, hold values between −1 and +1.

Since the objects' shape carries the most crucial information, that is to say what number it is, transitional values between black and white are most interesting in this case. A CNN would deduce a model from the training data that tries to understand the objects' shape.

It would be very complex to develop an algorithm that takes all observable pixel values deterministically into account. Numbers, especially when hand-written, can be tilted, stretched and compressed.

B. Rectified Linear Units Layer

As mentioned above, input layers are fully interconnected with following layers. Always processing every single value of previous layers leads to inefficiency, since we are only interested in the four’s shape and not in the white background nor the black filling. Knowing the object's shape that is in the image naturally tells us what number is shown in the picture.

To keep neural networks sparse, it is common practice to apply additional functions, called activation functions. They are biologically inspired in the way that a neuron (biologically and in terms of artificial neural networks) fires information, if a certain threshold is reached. Basically, every function can be used as such, but the most advantages, and therefore most used, are obtained by applying the sigmoid function, the hyperbolic tangent, or the rectified linear unit, also called rectifier. Their graphs are shown in figure 3.

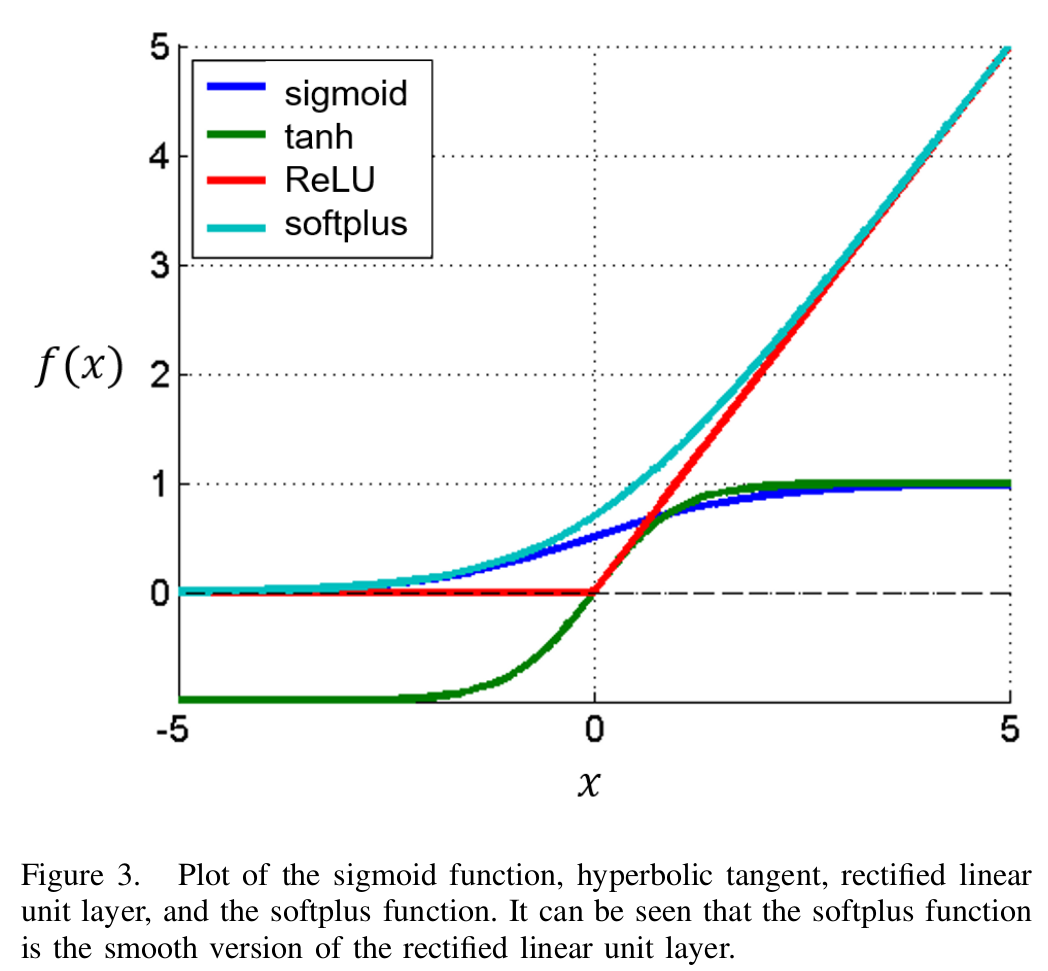
Explained briefly, these graphs tell us what value is propagated to the next layer. In the case of the rectifier linear unit, we can see that whenever the value that it obtains is smaller or equal to 0 the output value is 0. Subsequently, we get rid off all negative values which makes it much easier for the following layer to process due to less values (more scarce).

Indeed, the latter was the most popular activation function for deep neural networks in the year 2015. This is not a coincidence rather than justified by several reasons, such as the efficient computation of it.

A more efficient computation means that the learning phase is shorter. Often neural networks are trained several times faster just by choosing rectifier linear unit as an activation function.

Moreover, since we train deep neural networks by using gradients of the system - we will come back to this later on - rectified linear units don’t impose the problem of vanishing gradients. The vanishing gradient problem is imposed by functions which gradients get very close to zero and, thus, slow down the learning rate.

In comparison to the sigmoid function as well as the hyperbolic tangent, in the activated region of rectified linear units, which is the positive region, the derivative is defined to one (straight line).

Depending on the problem, it can be advantageous to activate neurons utilizing the softplus, the smooth version of the rectifier.

C. Convolutional Layer

Convolutional layers are the core of CNNs. They perform an image convolution of the output of the previous layer where the weights specify the convolutional filter.

The main goal of this layer is to use convolutions to identify a number of features that the objects have. Therefore, we perform a convolution of the input with a linear filter (a certain matrix for filtering effects in images), add a bias to adjust the activation threshold, and apply a non-linear function (this is the activation function).

The input of this layer can be a matrix with values from −1 to 1 as defined before that is either dense, for instance due to a fully interconnection with the input layer, or sparse, due to an applied activation function in the predecessor.

The non-linearity is helpful to capture classes that are hard to identify. It turned out that it enhances the abstraction ability of the model.

To achieve the goal of modeling high-level abstractions in data (this is needed for identifying more complex objects), we apply multiple convolutional layers. The first convolution layer obtains the low-level features, like edges, lines and corners, and the more layers the network has, the better it'll learn higher-level features.

D. Pooling Layer

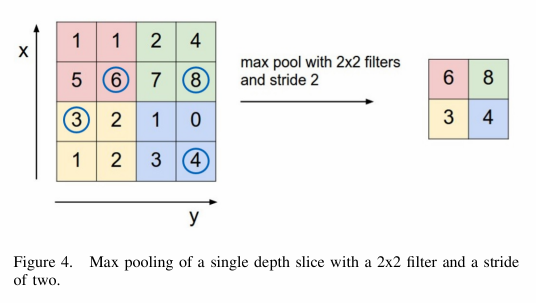
It is common to periodically insert pooling layers inbetween successive convolutional layers. By reducing the dimensionality, they reduce computational effort for upper layers and, further, a non-linear downsampling prevents possible overfitting of the system. Overfitting is a modeling error which occurs when a model is too closely fit to a limited set of data points. It generally takes the form of making an overly complex model to explain idiosyncrasies in the data under study.

The pooling layer can be realized in different ways, for instance shown in figure 4. Here we can see max-pooling. This means that for every second element we apply a 2x2 filter (mathematically speaking this is a matrix), which neglects all values but the largest within four elements. So, we downsize aka downsample the dimension of the data we are working with to a fourth of the size. In other approaches smallest values or values closest to the mean, which is calculated beforehand, are chosen.

E. Output Layer with Loss Function

The main purpose of the output layer is to evaluate the already processed data. There are many aspects of how to interpret this data and how to measure the loss, which is the parameter that is used to train our neural network. In essence, neural networks are firstly trained - thus the name self-learning systems. Once a certain accuracy is reached they can be used in production.

At the last layer of a deep CNN that trains on images to identify objects, we want to predict a single class out of a number of mutually exclusive classes and obtain the respective vector keeping the output values. These values identify what an image shows. In the output layer the number of neurons is equal to the number of the different classes of objects.

The output layer we present here is well-known as Softmax with Loss. ( Advanced and not crucial to know: the supporting function is the softmax, a multinomial logistic regression, so a generalization of a binomial regression.) Its ability to map a vector to a probability of a given output in binary classification (one or zero) is the reason we chose this one out of numerous possibilities.

The loss or cost function then calculates the loss in a supervised manner. Supervised means that in the training phase we know what the outcome should be (the vector is 1-hot encoded: everything is zero except the correct answer) and can use this to learn our model. Therefore we need labelled data.

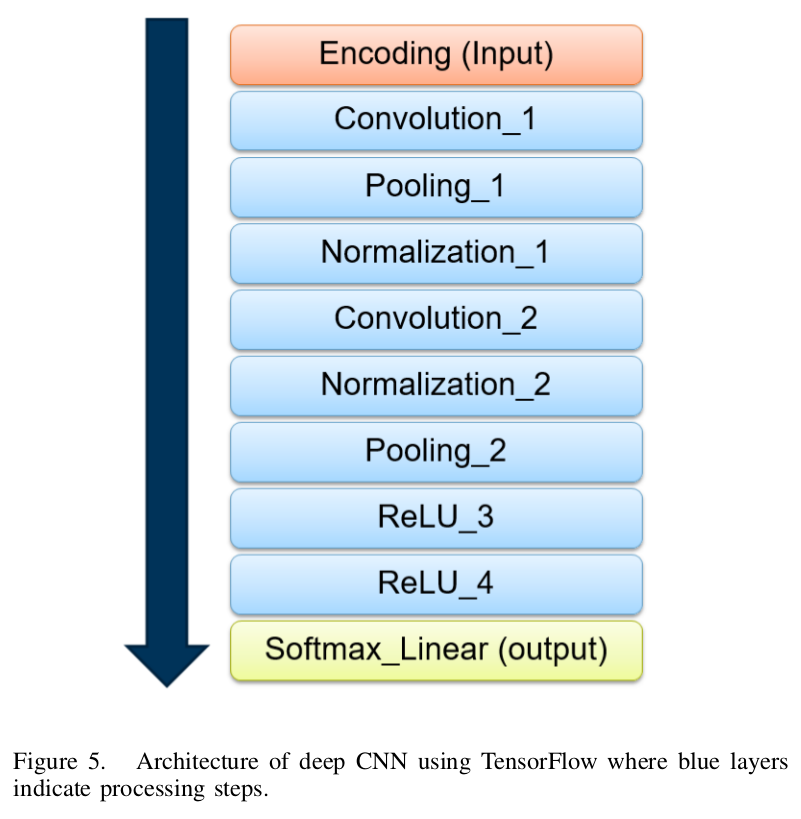
After describing all of our used layers, here is the overall architecture we are having:

F. Training of DNNs

In essence, deep learning means to minimize the loss calculated using the cross-entropy function (in our case). The optimization method we focus on in this section is gradient descent, also known as steepest descent.

In the simplest case we only have to optimize one single weight, so that the corresponding loss is one dimensional with one global minimum and, possibly, some local minima. In a normal-sized systems there are numerous weights to adapt - more than a million is not unusual. The corresponding loss function has thus as many dimensions and is computationally more expensive to optimize.

Updating the training values (minimizing the loss): the whole process is called backward propagation of errors.

However, within the deep learning community many different optimization methods are likely to be used, such as e.g. the conjugate gradient method, the L-BFGS algorithm (Limited-memory Broyden-Fletcher-Goldfarb-Shannon), and so forth. In an optimal case we find the loss’ global minimum in the most efficient manner.

---

NEXT PART: We use this CNN in training and evaluation mode using tensorflow.

I thrive to write quality blog posts here on steemit to really add value to this amazing platform. I believe that blockchain technologies are the future. I hope this format was good for you. If not, leave me a comment and I will work on it.

Further questions? Ask!

I am working on follow-up blog posts, so, stay tuned!

If you liked it so far, then like, resteem and follow me: @martinmusiol !

Thank you!

#deutsch