A: Is there a more systematic approach to classical mechanics than Newtons second law?
Hi guys. Today I am back with a whole new topic I have never talked about. I intend to do a lot of posts like this as I think it is very educational and I personally love solving problems in classical mechanics. A lot can be done analytically which is a true joy!
So let me answer the question I posted earlier. There is a simpler more systematic way of describing systems of classical objects and it is called The Lagrange Formalism. I wont talk about what it is as it is a very well described topic that you can find on the internet, but I do intend to showcase its strength in this post and some more posts coming in the future.
The central object of this formalism is the Lagrange function that is a generalized function of the coordinates of the objects in the system - qi - and its first time derivatives - qi,. It is defined as:
The T(qi, qi,) is the kinetic energy of the entire system and V(qi, qi,) is the potential energy of the system. Once you defined your L for your system, you can very easily get your complete set of equations of motion using:
I am sorry about the weird notation but Markdown is not very math friendy. δ stands for a partial derivative, while d/dt is the total time derivative.
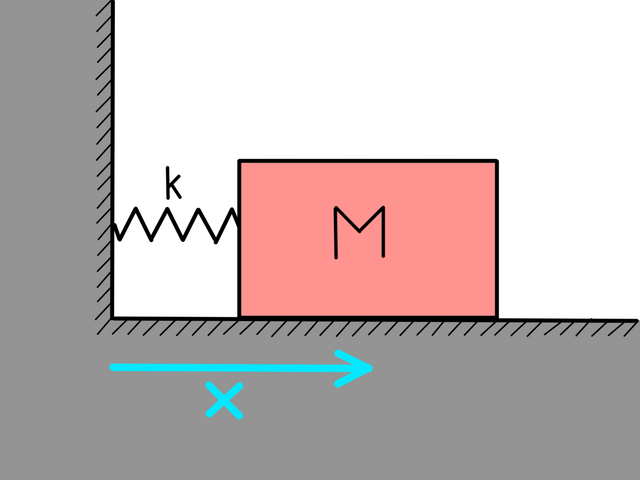
Lets look at a simple example of a mass tethered to a wall with a spring with its coefficient being k and its mass m. You can look at the sketch in the first picture above. The spring has a natural length of l. The kinetic and potential energies of such a system is:
Here we remembered that the velocity is defined as the first time derivative of the position - v = x,. Usually dots are used as time derivatives but it is impossible to use them here. For the next post I will think of something else. If you now use the recipe of how one derives the equations of motion you get:
You get the well known second law of motion derived by Newton. The Lagrangian formalism works. Yaaaay. Now we can use it for a more interesting case.
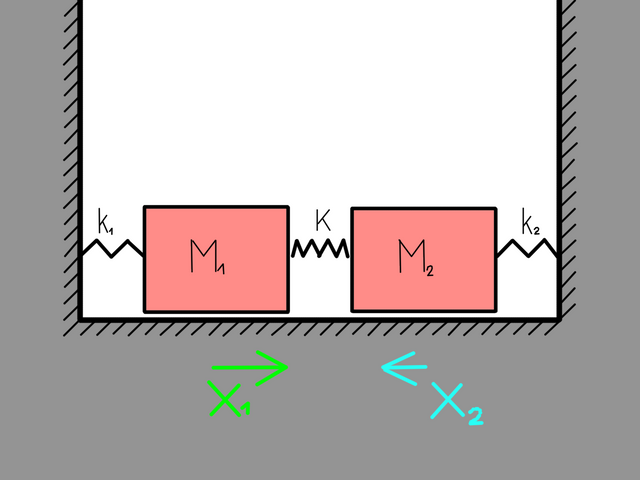
Lets look at a more complex system that contains two bodies with masses that are coupled together. Similarly as before we can easily write the Lagrange function for the system as:
The kinetic energy part is pretty self-explanatory. The potential energy is also not overly complicated but still a bit more thinking goes into it. The first two terms are the potential spring energies of the wall-mass couplings while the last term is the mass-mass coupling. If x1 = x2 then the middle spring didnt stretch. This is why there is a minus in the last term. If we again use the recipe we get the equations of motion:
Although there is a formalism that easily deals with such equations I will solve these equations using some magic. But first lets make a simplification just for calculation (and animation) sake. Lets say that:
This means we can define a characteristic frequency ω02 = k/m and we can write it to write a set of beautiful equations:
So here comes the magic so pay attention. We notice that there is a symmetry to the equations, which is why we define two new coordinates (x1 - x2) and (x1 + x2). We can write the equations of motion for these new coordinates by subtracting the old differential equations for the first of the new coordinates and by summing up the old equations for the second case. If we do this we get:
We recognize these equations of motion as equations of motion describing pendulums and similar harmonic oscillator things. We see that the sum has will oscillate with a frequency of ω0 while the other will oscillate with a frequency of about 2.23 ω0. But what are these coordinates actually representing.
Well let my gifs illustrate.
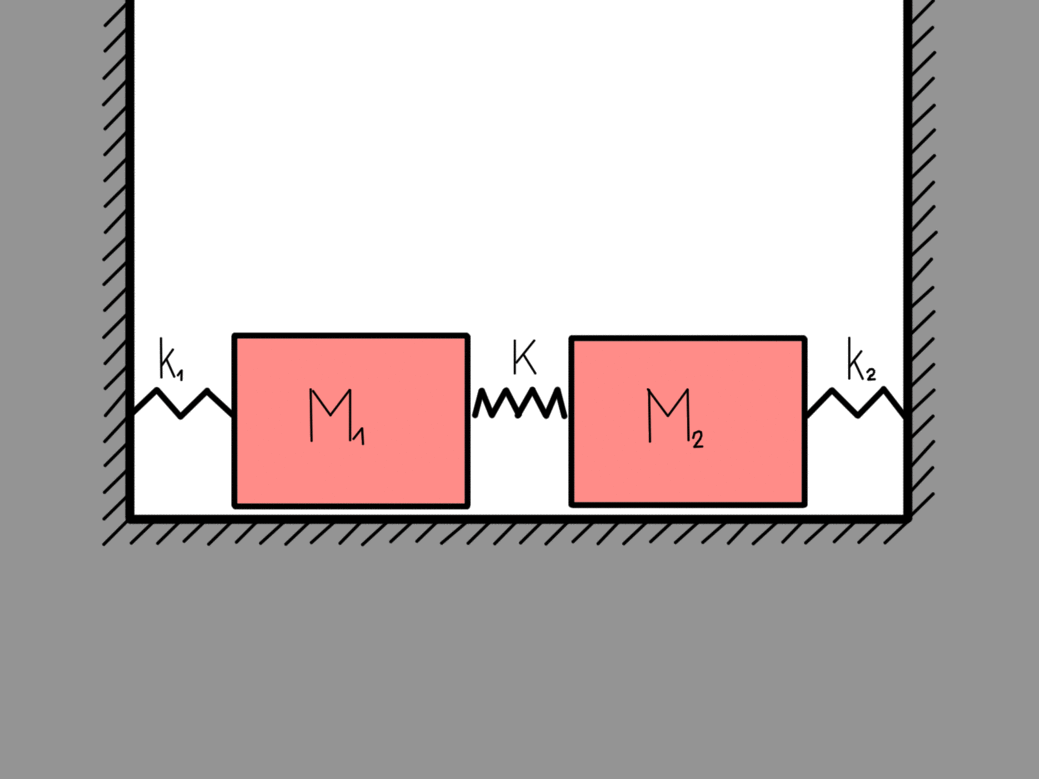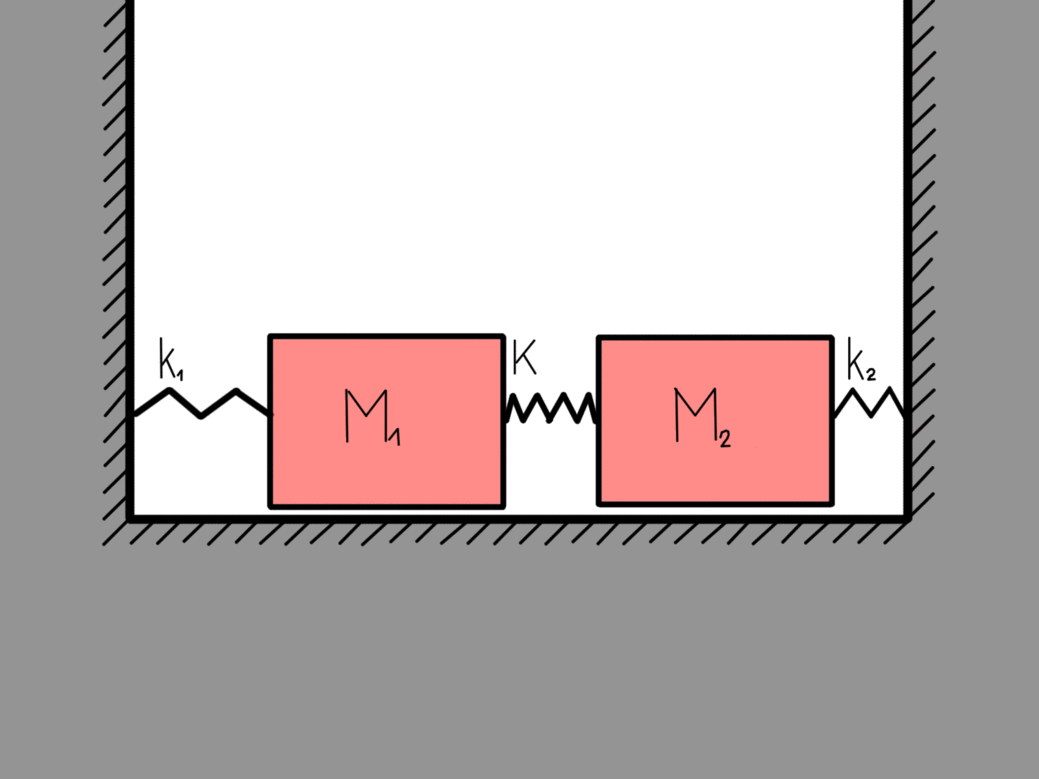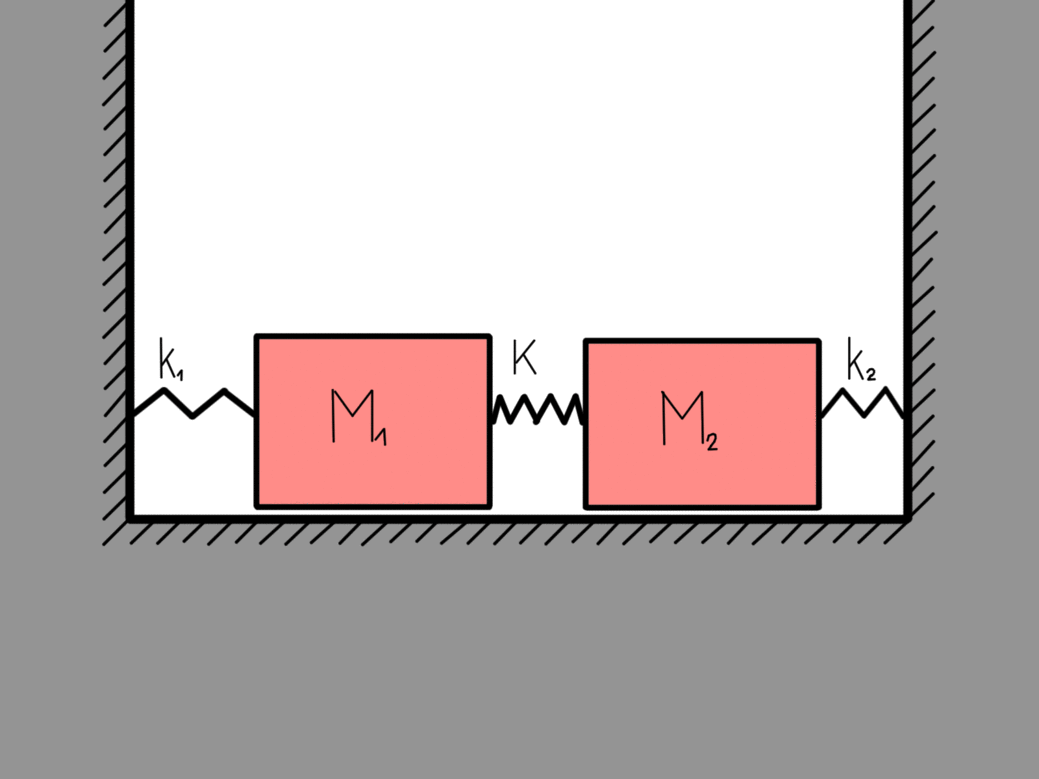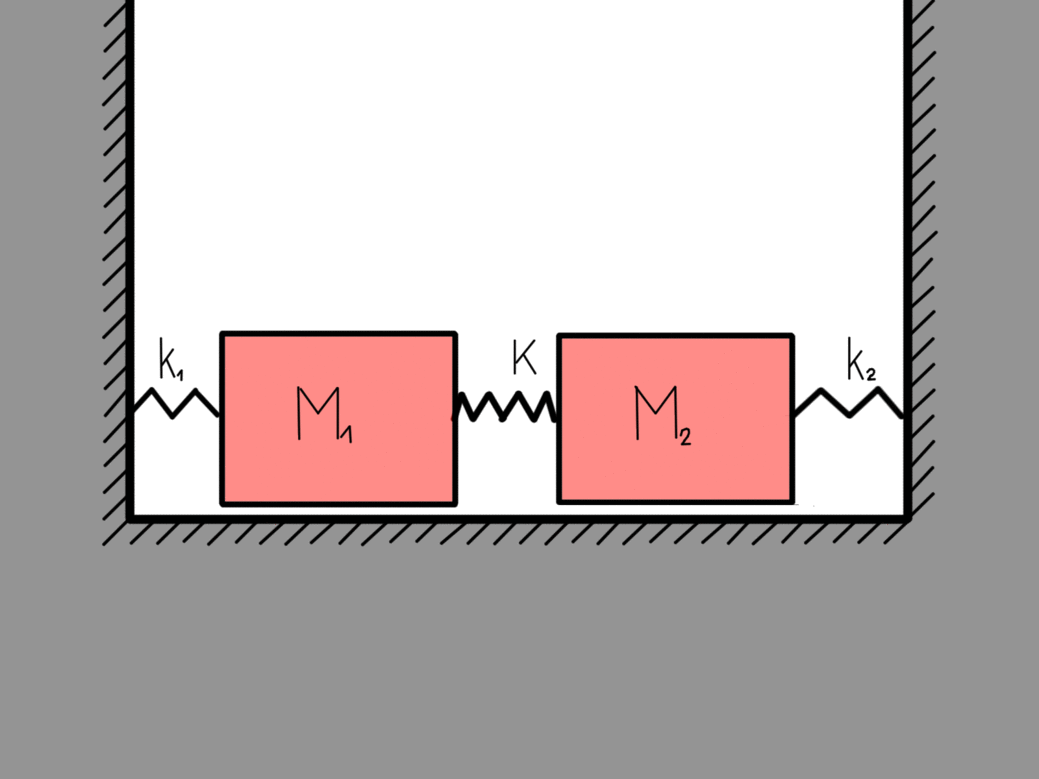
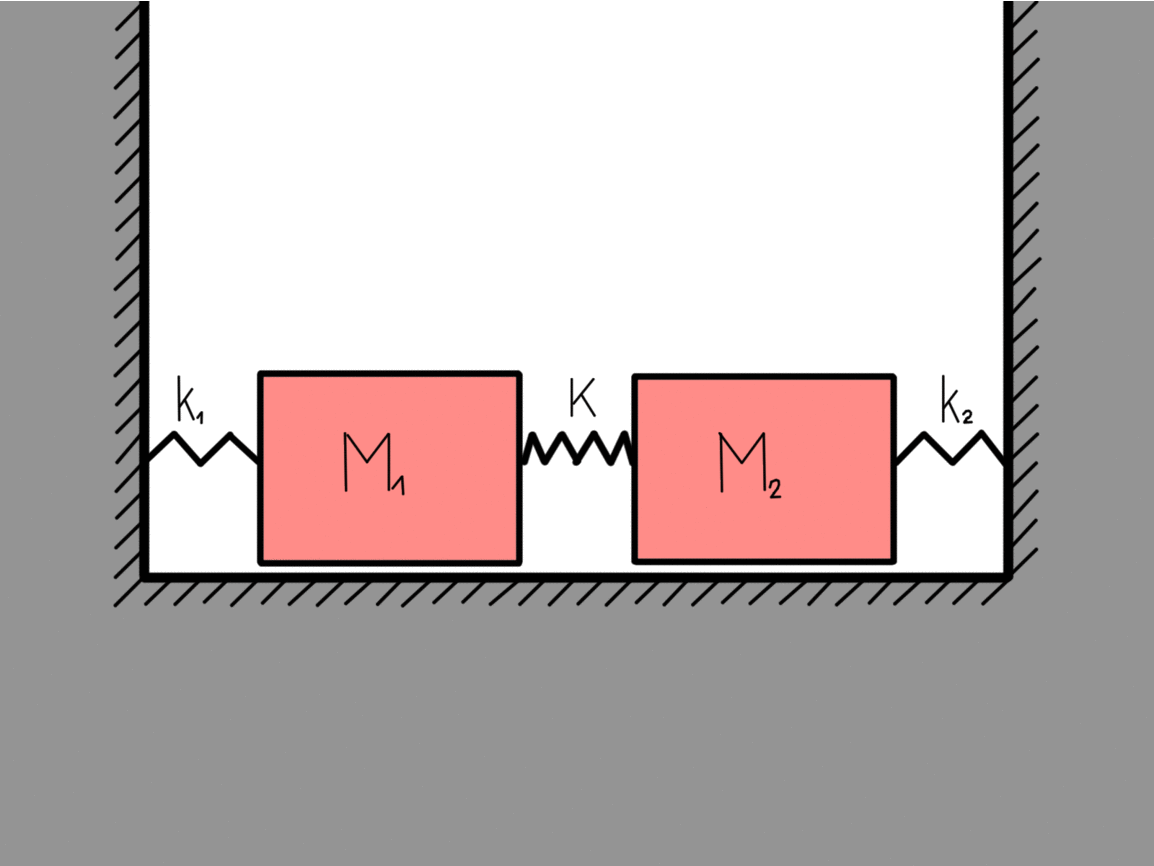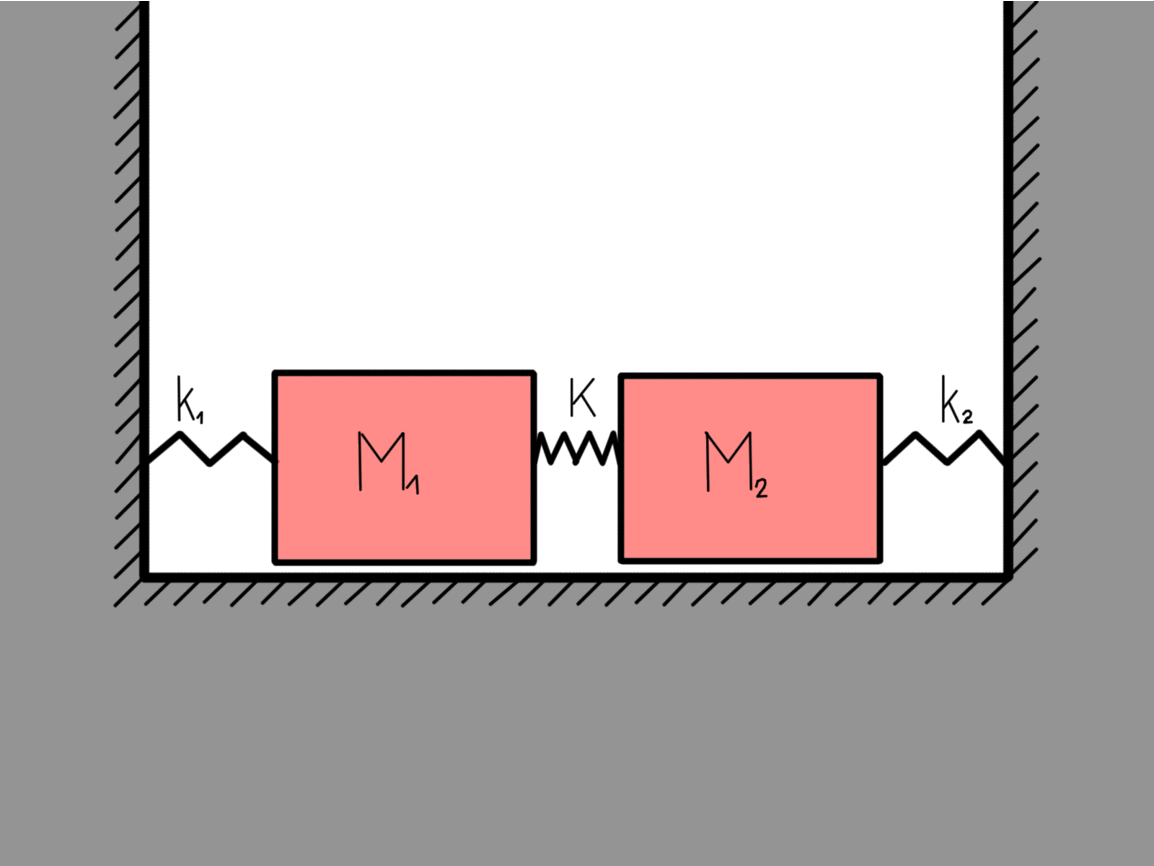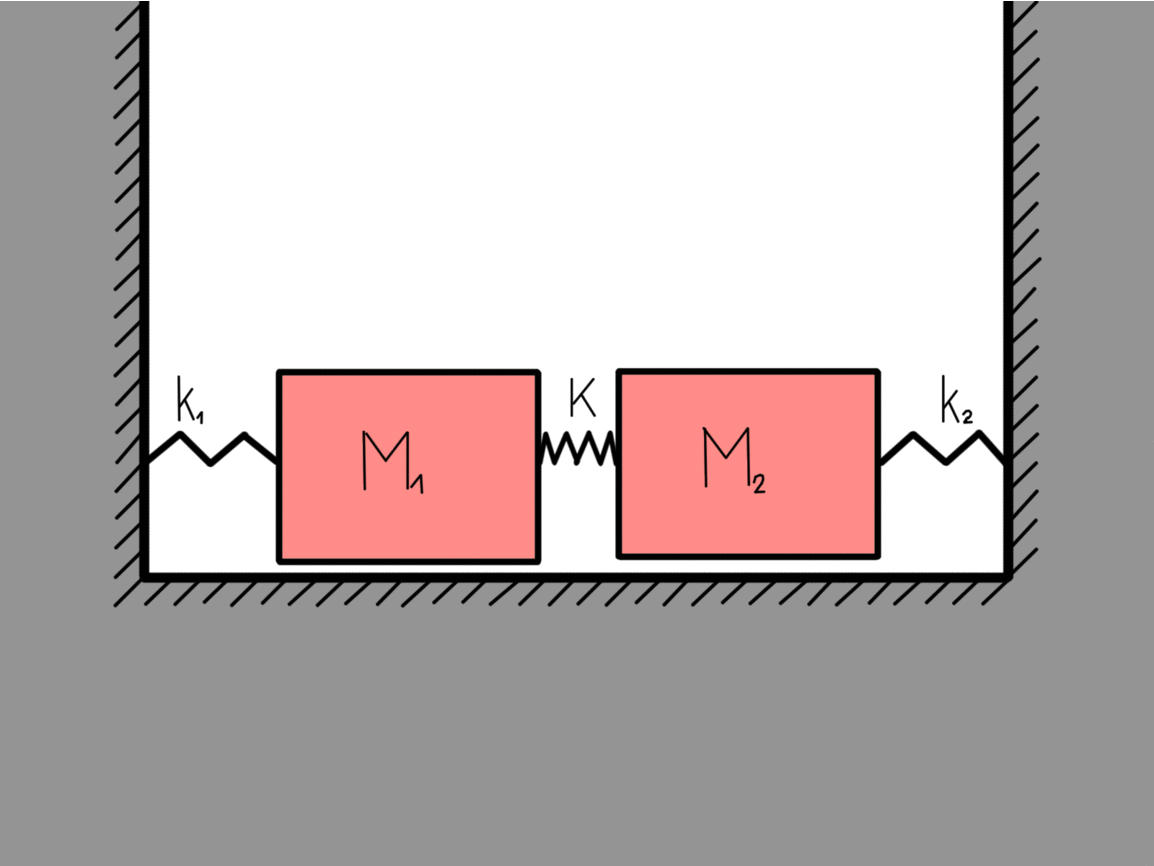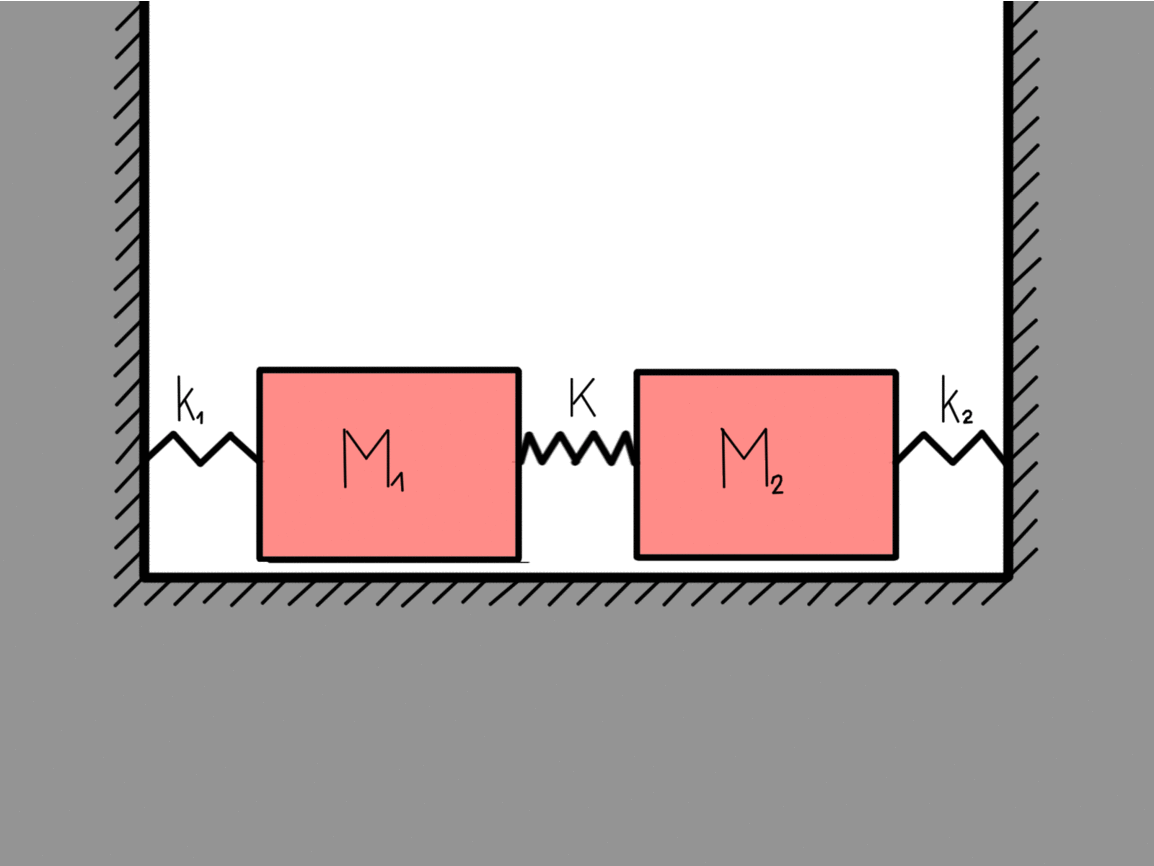
This is what we called the eigen-motions of a harmonic oscillator, which means that they are stable. If nothing disturbs them they will go on forever. All the other possible motions of this two-body coupled harmonic oscillator can be written as a linear sum of these two eigen-motions. The eigen-frequency ω0 is the frequency of the system when only the center of mass is moving (right figure) while the eigen-frequency 2.23 ω0 is the frequency of the system when the masses are moving towards each other (left figure).
Conclusion
I hope I was able to convince you that this is an easier way of deriving the equations of motion than using the classic Newtonian kinematics. Of course the results are the same and you still have to solve some differential equations, but the way of constructing the differential equations is more systematic. I suggest you do the calculations alone the old way and the Lagrangian formalism way I introduced here for the coupled oscillator problem. You will see it is much easier this way.
I intend to bring you more interesting systems of coupled "stuff". I think it is really fun solving such easy problems that are really rich with physics.


StemQ Notice: This post was originally submitted on StemQ.io, a Q&A application for STEM subjects powered by the Steem blockchain.
@maticpecovnik, tvoja objava je dobila 100% upvote od @teamslovenia!
Kako dobiti upvote?
⚫ Pridruži se nam v Discord strežniku!
⚫ Uporabi TeamSlovenia upvote bot!
Kako lahko tudi ti pomagaš, da bo @teamslovenia bot močnejši?
⚫ Delegiraj steem power - 50 SP - 100 SP - 500 SP - 1000 SP - Po želji!
⚫ Sledi upvotom od @teamslovenia - Navodila
Ta projekt podpira Steem Witness @fbslo - Glasuj zdaj!
Great tutorial mate and the gifs are just wow :D How can I make so as well. Any advice :) ?
Thank you very much. I hope it was understandable. I know I skipped some steps but I really cant write it all.
It really just takes time and patience. And sime practice. I use a free software called Krita. Try it.
Posted using Partiko Android
Thanks :) It was understandable :)
Congratulations @maticpecovnik! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Hi, @maticpecovnik!
You just got a 2.66% upvote from SteemPlus!
To get higher upvotes, earn more SteemPlus Points (SPP). On your Steemit wallet, check your SPP balance and click on "How to earn SPP?" to find out all the ways to earn.
If you're not using SteemPlus yet, please check our last posts in here to see the many ways in which SteemPlus can improve your Steem experience on Steemit and Busy.
Hi @maticpecovnik!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 2.913 which ranks you at #11187 across all Steem accounts.
Your rank has improved 345 places in the last three days (old rank 11532).
In our last Algorithmic Curation Round, consisting of 271 contributions, your post is ranked at #138.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Congratulations @maticpecovnik! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPHi @maticpecovnik!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations @maticpecovnik! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOP