Introduction To Circuit Theory - Charges, Voltage And Current

Charges have always been linked to the concept of electricity right from the very start. As far back as 600 B.C, it was discovered that if the fossil resin was rubbed with a dry substance, it was found that the amber could exert a force of attraction on a light material in the form of a feather.

^{Wikimedia Creative Commons: How Flow of Charges Result To Electicity}

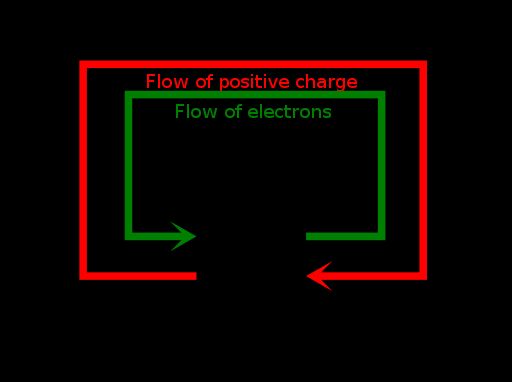
In reality, the word electricity was derived from the Greek word for amber called elektron. In this case, the amber was demonstrated to possess frictional electricity acquired through the accumulation of charge.

Until towards the end of the eighteen century, this happened to be the only form of electricity recognized by man. In 1999, Alessandro Volta made a breakthrough and discovered copper-zinc battery, which he demonstrated to have the ability to produce electricity consistently flowing in a wire. At that time, this type of electricity was called current electricity to differentiate it from the frictional kind. Volta, in the course of series of experiments, was able to show that the two types are quite the same, judging from the result he got.
Fortunately, today we can vindicate Volta from our knowledge of the atomic structure of matter.

Concerning atomic description, all matter is composed of atoms. The atom constitutes a central body called nucleus and some electrons orbiting round the nucleus. This electron is responsible for most properties of engineering materials depending on electronic configuration.

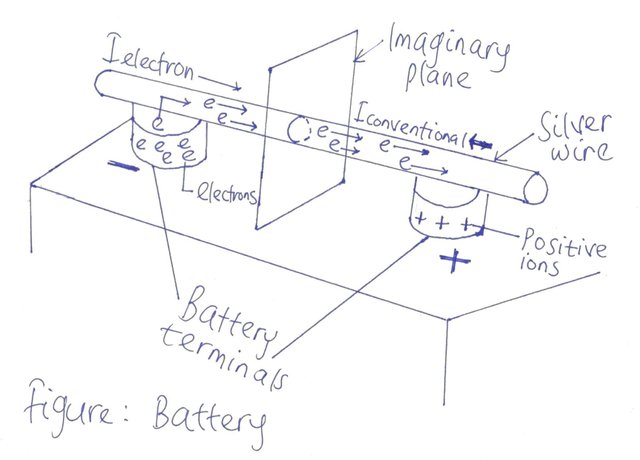
Let us consider a small length of silver wire that is dissected with a fictitious perpendicular plane showing the circular cross-section. At room temperature without the application of external pressure, you would notice the free electrons will drift in different direction owing to the thermal energy absorbed from the ambience.

When an atom let go of its free electrons, it will acquire a net positive charge which is called positive ion. The electron can navigate through the positive ion and leave the general vicinity of the parent atom while the positive ion will only vibrate in a mean fixed position. Based on this observation, free electrons are the charge carrier in silver or any other solid conductor of electricity.

When you consider the diagram below, you will notice the randomized movement of electrons which results in perpetual gaining and losing of energy by the fact that they change direction and velocity. Some of the causes of this random movement include:

• The collision between the positive ion and the free electrons
  the force of attraction existing between the positive ion and the free electrons.

• The repulsive force that exists between the electrons.

• The random motion of free electrons is in such a way that when you consider a length of silver wire, the number of the electron moving from right to left will equal the one that will be moving from left to right.

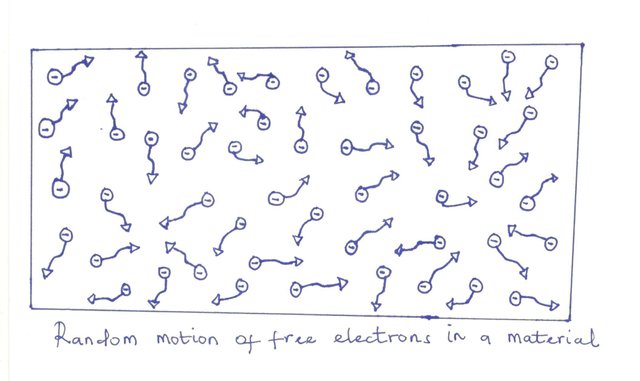
One can then conclude that with no application of external pressure, the net flow of charge in any one direction equates to zero.
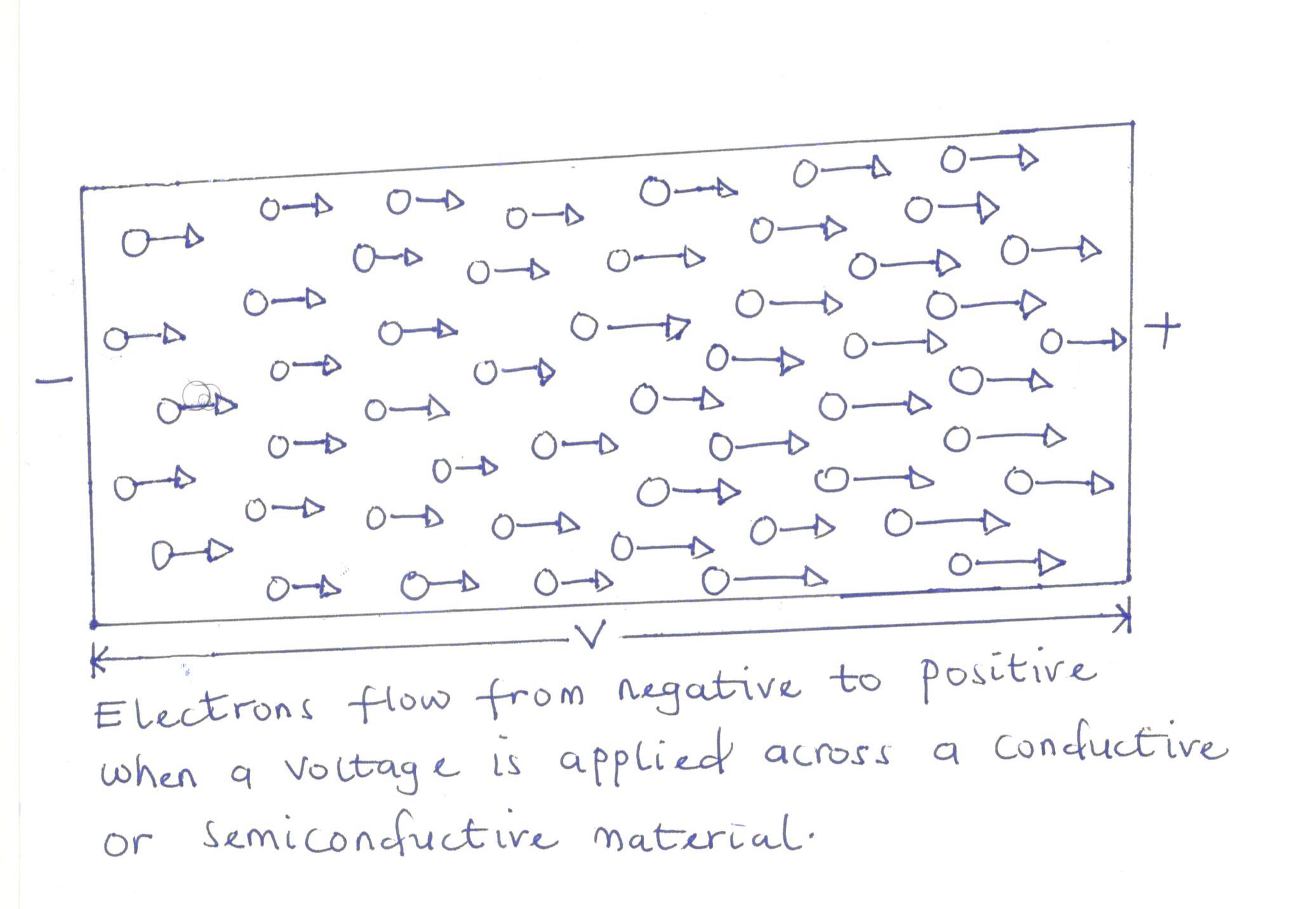
Let us now connect the two ends of the wire between the battery terminals as depicted below. The battery exploits its chemical action to place a net positive charge on one terminal and a net negative charge on the other.

The moment the wire is connected between these two terminals, the free electrons inherent in the silver will drift towards the positive side of the battery, while the positive ion will keep vibrating in a mean fixed position. The negative terminal serves as a source to be drawn from when the electron of the silver moves towards the positive terminal.

The chemical activity of the battery will consume the electrons at the positive terminal and ensures a consistent supply of electrons at the negative end.

CURRENT

Assuming 6.242× 10¹⁸ electrons moves at uniform velocity through the imaginary cross-section of the figure below in 1 second, the flow of charge or current is said to be 1 Ampere. The current associated with only a few electrons per second would be insignificant and of little practical consideration. To establish numerical values that permit immediate comparison between levels, a Coulomb (C) of charge was defined as the total charge associated with 6.242× 10¹⁸ electrons. The charge associated with one electron can be calculated from simple proportion.

For example: Since 6.242× 10¹⁸ electrons is associated with 1 Coulomb of charge. It therefore means that 1 electron will give 1C/(6.242× 10¹⁸ electrons) × 1 electron
It therefore means that a charge of 1.602 × 10^-19 is associated with one electron.

There is a relation between charge, current and time which is as given below:
Charge (Q)= Current (I) × Time (t)

Consider the example below:

Determine the time required for 6× 10¹⁶ electrons to pass through the imaginary surface of the figure above if the current is 4mA.

SOLUTION
Since 6.242× 10¹⁸ electrons is associated with 1C of charge, then 6× 10¹⁶ electrons will yield: 1C/(6.242× 10¹⁸ electrons) × 6× 10¹⁶ electrons
=0.00961C
But Q=It, thus t=Q/I = 0.00961C/(4×10^-3) = 2.4025S

Circuit

An electric circuit is a closed path, composed of active and passive elements, to which current flow is confined. The figure below depicts a typical circuit containing one passive and one active element. An active element is one which supplies energy to the circuit. Passive elements absorb energy and then either convert it to heat or stores it in an electric or magnetic field. The battery in the figure below is the active element. The resistor is a passive element.

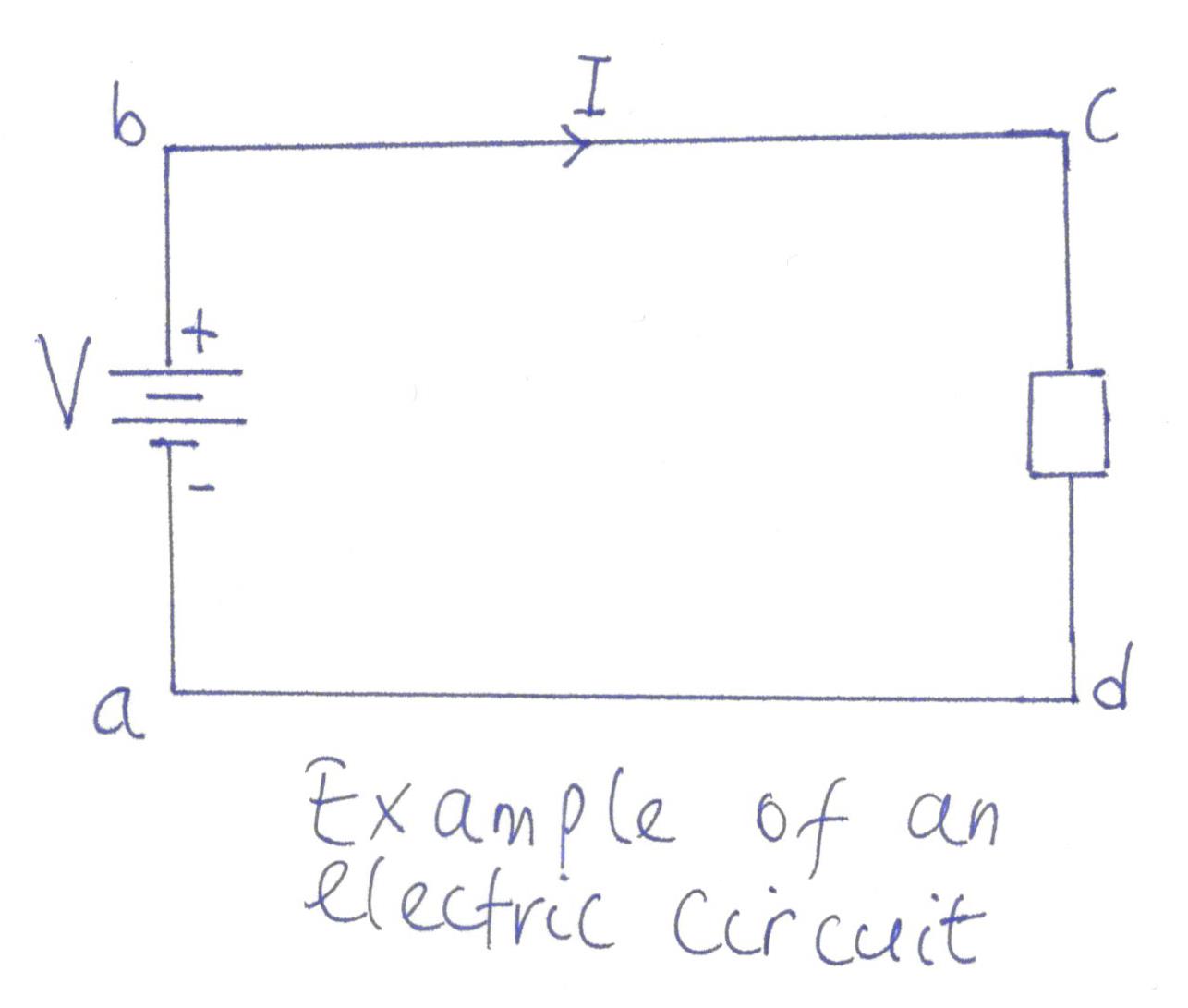
The electric circuit theory is developed from five basic laws: Coulomb’s law which leads to the concept of capacitance; Ohm’s law which leads to the concept of resistance; Faradays law which leads to the concept of inductance and lastly Kirchhoff’’s voltage and current laws, which embraces the first three laws and provides a system of formulation of the principles in solving numerous circuit problems.

Let us consider the diagram of the figure below.

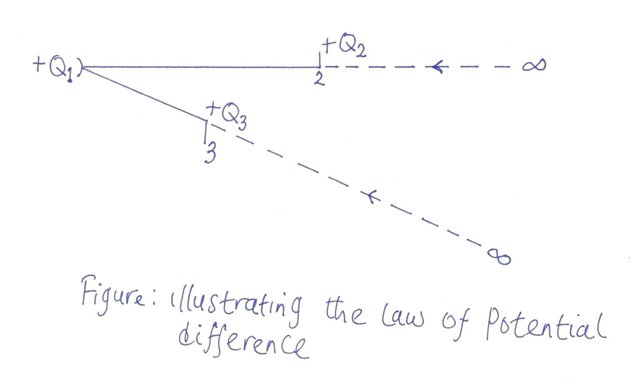
Let us assume that charge Q₁ is located at some fixed point in space. The charge Q₂ is assumed initially to be on a horizontal path from Q₁but infinitely far away. Such placement removes any force of repulsion that could exist between Q₁ and Q₂ and thus, force of attraction is zero. Let us consider next what happens as Q₂ is moved from infinity to a point where it is finally located r₂ meters from Q₁.

It should be evident that as Q₂ is moved in this direct line from infinity to positions which are closer and closer to Q₁, greater and greater forces are required to accomplish this, and this force is as a result of force of repulsion because Q₂ is now in a positon closer to where it will experience the electric field of Q₁.

Also, since the force exerted on Q₂ acts through a distance which measures from infinity right up to r₂, it follows that work is being done on Q₂.This work is imparted to Q₂ in the form of potential energy, which is recoverable in the form of kinetic energy assuming the force holding Q₂ fixed at a position r₂ meters from Q₁ is removed. Remember that the two charges are of opposite polarity and there exists a force of repulsion between Q₁ and Q₂ which attempts to send Q₂ back to infinity.

The fact that work must be done on Q₂ to bring it from infinity to r₂ may also be described in terms of the electric field intensity associated with charge Q₁.With regards to Q₁ an electric field that diminishes in magnitude exists from r₂ to ∞. In moving Q₂ from ∞ to r₂ work must be done against this electric field.

V₂ is the work imparted per coulomb of charge in moving Q₂ from infinity to r₂ which can be expressed mathematically as work done per unit charge.

Voltage=Work/Charge

Where W is expressed in Joules (J) and Q is in Coulombs (C)
The unit of voltage is the Volt which has symbol V.
One volt is the potential difference (voltage) between two points when one joule of energy is used to move a Coulomb of charge from one point to another.

In this particular example, V₂ =(W₂)/(Q₂)

To clarify the meaning of potential difference, let us refer back to the diagram, assuming we move another charge from infinity to r₃. It is easy to see that r₃ is smaller than r₂. And as such more work will have to be expended to position a charge at point 3.

The potential at point 3 will be, V₃ =(W₃)/(Q₃)
Because V₃ is greater than V₂, there exists a potential difference between these two points. Based on the above fact, whenever a unit charge moves from the point of higher potential (point 3) to the point of lower potential (point 2), it gives up energy. On the hand, when a unit charge moves from the point of lower potential to one of higher potential it receives energy. This analogy is often applied to the solution of electric circuit by the method of Kirchhoff’s voltage law in which voltage rise or voltage drop often come into play in mesh analysis.

To illustrate the above point, refer to the diagram of the circuit above.The charges will flow out from the positive part of the battery. If we assume clockwise convention of flow, it then means that as the charges move through, the voltage rises from a to b thus receiving energy. The voltage rise makes the potential of b to be higher than that of a .But as they move from c to d, they undergo a voltage drop, thereby losing energy to the resistor appearing between these two points.

It is worthy to remember that the stream of charge gains energy in one part of the circuit (at the active element) and gives it up at the other part (the passive element). In the end, the total energy remains unchanged in accordance with the law of conservation of energy.

Consider the examples below:

• Find the potential difference between two points in an electrical system if 90J of energy is expended by a charge of 30C between these two points.

SOLUTION
V= W/Q=90J/30C=3V

• Determine the energy expended moving 40µC through a potential difference of 8V.

SOLUTION

W=QV= 40 × (10^-6) (8) = 320 × 10^-6 J=320 µJ

Voltage could be further explained as below which is not as mathematical as the above illustration.

There is a force of attraction between a positive and a negative charge. A certain amount of work would have to be done to counteract the force and propel the charge a certain distance apart. All opposite charges have certain potential energy as a result of the distance between them. The difference in potential energy of the charges is the potential difference or voltage. Voltage is the driving force in electric circuits and is what produces current.

Consider an overhead tank, which is like 20m above the ground. A certain amount of energy is needed to pump the water up to fill the tank. Once the overhead tank is filled, the water in it will possess a certain amount of potential energy which if released, can do some useful work. This form of energy is harnessed in the hydroelectric power plant where the water can be allowed to fall down a channel to turn a water wheel.

Just like in the overhead tank analogy, if a mass (m) is raised to some height (h) which is above a reference plane, it has a measure of potential energy expressed in Joules (J) which is W (potential energy) = mgh

This mass has the potential to do work such as crush an object placed on the reference plane. If the weight is raised further, it will have an increased measure of potential energy and can do additional work. There is a clear difference in potential between the two heights above the reference plane.

REFERENCES

1. Difference between Current and Voltage
2. Basic Concepts of Electricity
3. Electric Potential Difference