TÉCNICAS EN COMUNICACIONES DIGITALES – MULTIPLEXACIÓN POR DIVISIÓN DE FRECUENCIAS ORTOGONALES (OFDM)

La demanda consumista de tecnología ha tenido un crecimiento exponencial en los últimos años, se exige cada vez más a los sistemas de transmisión mayores prestaciones que logren satisfacer las necesidades de los usuarios, por tanto las medidas e implementaciones de ingeniera son renovadas constantemente concibiendo así técnicas de transmisión más elaboradas y sofisticadas.

En este caso particular, se plantea la Modulación por División de Frecuencias Ortogonales OFDM, técnica empleada mayormente en sistemas de radiofrecuencias, pero que está teniendo una gran aceptación para complementar a los “medios guiados” como es el caso de la fibra óptica; el objetivo de este texto es introducir el concepto de OFDM de una forma teórica/matemática la cual servirá para describir sistemas prácticos reales que emplean esta modulación.

Fuente

Abordando la concepción de OFDM, se define como una técnica de comunicación perteneciente al conjunto de “Modulación de Multiportadora (MCM)” , es decir, hace uso de varias señales portadoras que constan de tasas relativamente bajas para la transición de información, posteriormente con la adición en paralelo de las “subportadoras” se puede obtener una velocidad de transmisión de datos más elevada en comparación con otras modulaciones que utilizan el principio de MCM, además presenta una gran inmunidad ante la dispersión propia del canal.

Se analizan algunas situaciones que conllevan al uso de OFDM:
Al partir de un análisis sencillo de Canal vs frecuencia se puede evidenciar lo siguiente:

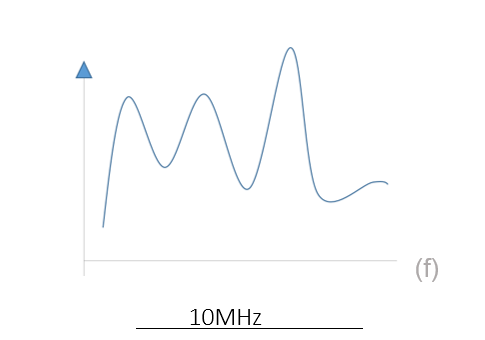
Figura N°1 Grafico de la respuesta de un canal en frecuencia de 10MHz – Elaboración propia

Dada la figura mostrada y considerando porciones de anchos de banda debidamente seleccionados o específicos, las variaciones en frecuencias son despreciables, no obstante al aumentar el ancho de banda que estamos analizando, en este caso concreto a 10MHz, es evidente que existen desvanecimientos frecuenciales, esto da cabida a una interpretación práctica, la cual si lo llevamos al dominio del tiempo se infiere que:

Figura N°2 Transmisión de un símbolo afectado por un eco en el tempo – Elaboración Propia
El rectángulo azul representa el símbolo y el cuadro anaranjado representa el eco que se produce
Dada las multitrayectorias que establecen las señales en la transmisión, existirán partes de la señal original que tomaran una ruta alterna, esto produce que la señal incidente en el receptor presente “ecos” afectando así la inteligibilidad de la comunicación; al darse estos desfases, los símbolos que son transmitidos se solaparan unos con otros conforme el receptor valla captando las señales; formalmente este efecto es conocido como Interferencia Intersimbólica (ISI).

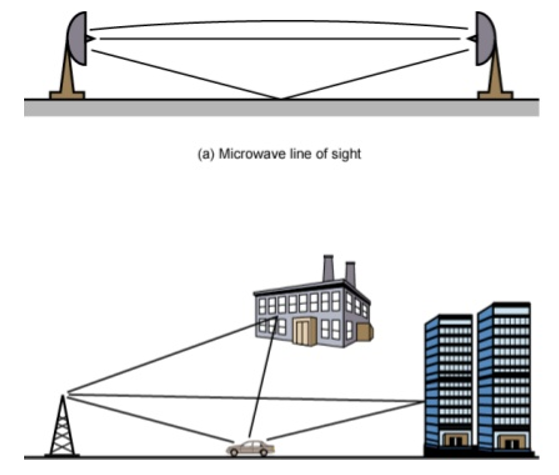
Figura N°3 Efecto de Multitrayectoria –Fuente

Pues bien, esto en pocas palabras significa que cuando el ancho de banda es relativamente pequeño los símbolos transmitidos serán lo suficientemente grandes para que el eco generado no afecte la comunicación, por el contrario si el sistema opera con anchos de banda mayores, la velocidad de transmisión será mayor por tanto existirán mas símbolos por segundo (de menor tamaño) pero los ecos se mantendrán igual de largos, concluyendo así en una interferencia que imposibilitara la comunicación.

Dado el comportamiento descrito anteriormente, se plantean variantes de modulación más efectivas:

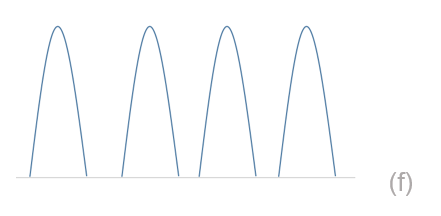
Figura N°4 Modulación por división en frecuencias contiguas – Elaboración Propia
Se puede hacer uso de una modulación con subportadoras contiguas (pequeñas) por ejemplo de 200 KHz, (muy común en GSM ), el inconveniente es que tenemos anchos de banda no utilizados (separaciones vacías entre las ondas ) lo que supone un desperdicio de la capacidad espectral , sin mencionar que la configuración electrónica de los receptores debe tener cierto grado de complejidad pues filtrar cada una de las portadoras resulta bastante comprometedor.

OFDM por su parte permite que estas portadoras sean ortogonales unas con otras, así el ancho de banda puede ser aprovechado de una forma más eficiente, además, como cada subportadora llevara consigo un símbolo, al sumar estos flujos de datos resulta que el tiempo total de símbolo será lo suficientemente grande como para que el ISI no afecte significantemente la transmisión.

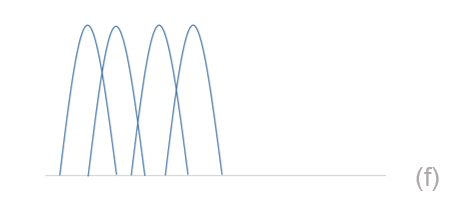
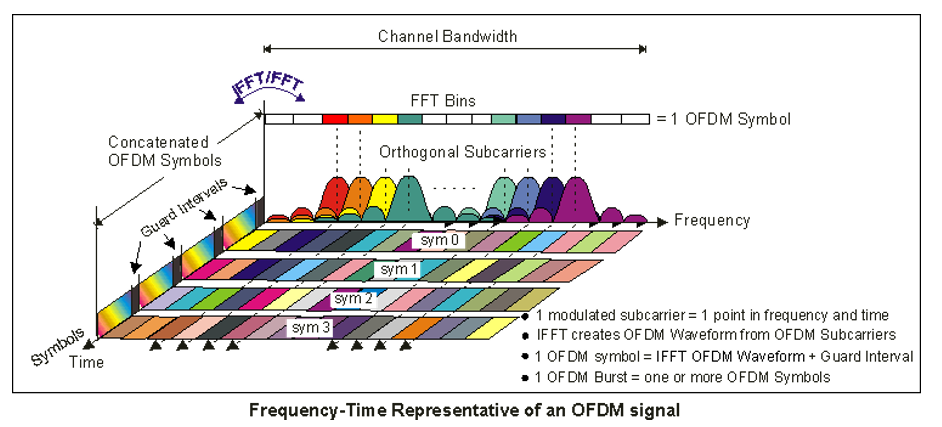
Figura N°5 Modulación por División en Frecuencia Ortogonal – Elaboración Propia

Una de las grandes prestaciones con las que cuneta OFDM, es la inclusión de lo que se denomina como “Intervalo de Guarda”, en concreto es una porción de tiempo que se añade al final de cada símbolo de manera que este último presente una duración más prolongada (lo suficiente) y así los ecos no afecten las señales en recepción.

Describiendo más en detalle lo anteriormente dicho, se puede afirmar que si el tiempo de procesamiento de los símbolos con que cuenta un receptor no es lo suficientemente eficaz para discriminar cada uno de los símbolos, tendremos ISI, por tanto esta duración se extiende de manera que el periodo de integración en el receptor sea excedido, cabe destacar que la porción añadida en el principio del símbolo más reciente es exactamente igual a la longitud final del segmento anterior , la siguiente figura ilustra esta afirmación:

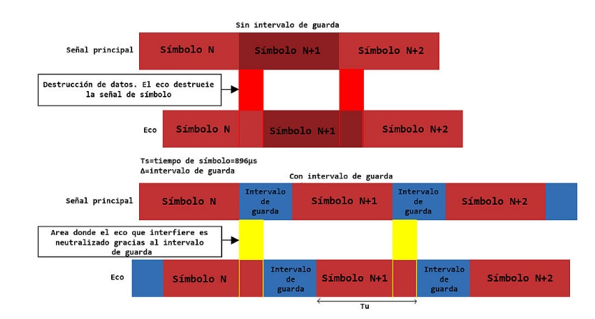
Figura N°6 Representación de los intervalos de Guarda en la transmisión de símbolos – Fuente

Para describir de una manera más fácil este proceso, se emite la siguiente analogía:
Imagine que se encuentra en un valle donde el eco producido por cada una de las palabras que dice en voz alta es tan grande que una palabra no se distingue de la anterior, este efecto será incrementa si usted hablara mucho más rápido, por tanto si quisiera que sus palabras fueran entendibles lo que debe hacer es decir una palabra y esperar un tiempo de manera que el eco se disipe en dicho tiempo de espera y entonces pueda decir otra palabra; en este caso las palabras serían los símbolos y el tiempo de espera entre palabras seria el intervalo de guarda.

Dependerá de la ingeniería aplicada al sistema de comunicación la implementación de intervalos de guardas más o menos prolongados, dado que si el tiempo de cada intervalo es muy grande la tasa de errores será menor pero en desventaja las velocidades de transmisión serán mas lentas, por el contrario si el intervalo es muy pequeño el sistema tendrá velocidades más rápidas pero con una alta susceptibilidad a el ISI.

Ahora bien, una vez comprendido el funcionamiento y aspectos básicos de OFDM, se procede a especificar el modelaje matemático que enmascara esta tecnología; el estudio completo de las ecuaciones que rigen OFDM involucra destrezas de un grado especifico, por lo que se recomienda a los lectores, el repaso de nociones como: números complejos, Transformadas de Fourier, funciones trigonométricas cardinales, etc.

Como se dijo en un principio, OFDM es una señal compuesta por la suma de múltiples subportadoras, de las cuales cada una transportara un trozo de información, o más formalmente transportaran “símbolos”, entonces la señal completa de OFDM se define como:

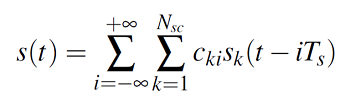
Donde:
s(t)= Señal OFDM
Cki= i-ésimo símbolo de la k-ésima subportadora
Sk= forma de onda para la subportadora k-ésima
Nsc= número de subportadoras
Ts= periodo de cada símbolo
A su vez la forma de onda con función definida Sk(t) viene dada por:

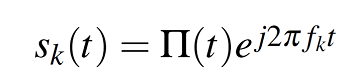
Donde:
fk= frecuencia de la subportadora
Π(t)= función de tren de pulsos
El termino fesorial de la derecha de esta última ecuación se especificara con mas detalle.

La clave del funcionamiento de OFDM se basa en el establecimiento de flujos de símbolos con periodos de tiempo grandes para que el ISI sea despreciable, pero ¿Cómo se logra esto?
Para entenderlo de una manera más objetiva se debe hacer un análisis a la función de pulso:
La siguiente imagen representa una ventana temporal (función pulso) la cual está definida por:

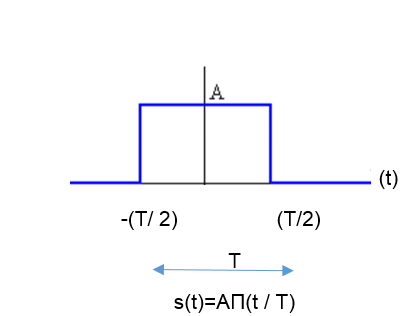
Figura N°7 Función de un Pulso temporal – Fuente

Esta es una señal que se encuentra activa durante un periodo de tiempo T y luego es nula fuera del intervalo que denota la figura .
Se procede con el análisis en frecuencia de esta función, por lo que se aplica la transformada de Fourier del pulso:

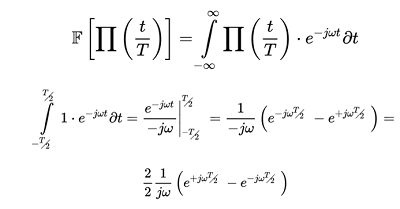
La expresión resultante entre paréntesis cumple con la forma de:

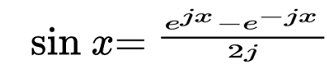
Entonces quedaría:

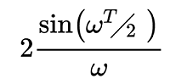
Esta ecuación puede ser rescrita en términos de la función sinc () (seno cardinal)
Consideraciones previas de la función sinc()

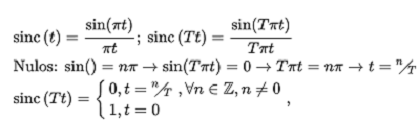
Finalmente se tiene que:

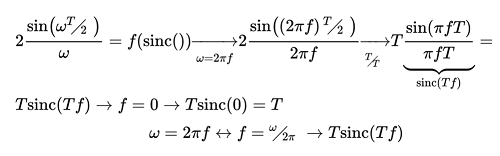
La transformada de Fourier esta dada por :

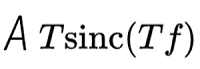
La expresión final queda multiplicada por A, pues es la amplitud del pulso.
La gráfica de esta función tiene la siguiente forma:

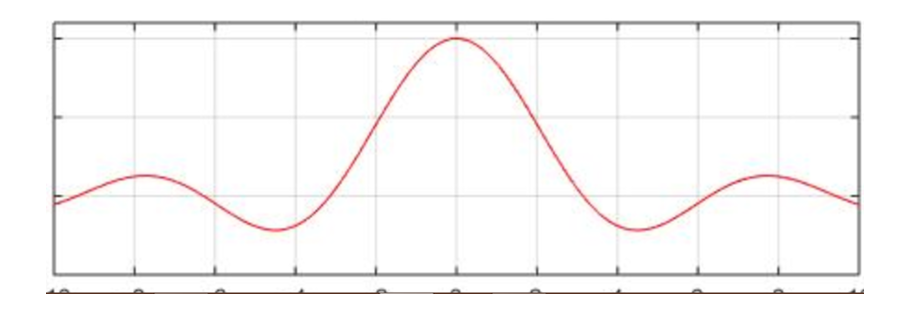
Figura N°8 Función Sinc – Fuente

La amplitud de esta forma de onda resultante es AT y sus puntos nulos (lo más importante) se encuentran en 1/T, 2/T, 3/T … N/T. Entonces se pudiera añadir justo al lado otra forma de onda idéntica a la de la figura, con la condición que la separación en frecuencia sea 1/T; esto se traduce en que la ventana temporal que se analizó previamente multiplicara a cada uno de los símbolos que se añadan:

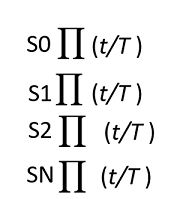
“S” representa un símbolo.
Al realizar esta multiplicación en el tiempo lo que se hace es generar muchas formas de onda en el mismo espectro cuya amplitud está definida por el símbolo, pero aún falta un ingrediente esencial, es decir, hace falta que esta señales no se molesten entre sí por lo que deben colocarse a frecuencias distintas (modularlas), para ello la transformada de Fourier original del pulso se deja intacta y la siguiente se multiplica por :

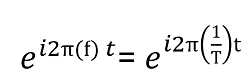
Nótese que se ha sustituido la frecuencia por 1/T , por tanto se ha logrado explicar el por qué de la función Sk(t) de la cual se hizo referencia previamente.
Se tendría que seguir multiplicando por múltiplos de 1/T conforme se vallan creando más señales:

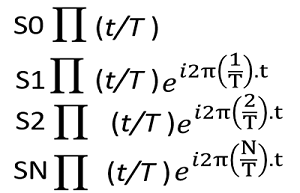
Vista en una gráfica se vería algo como:

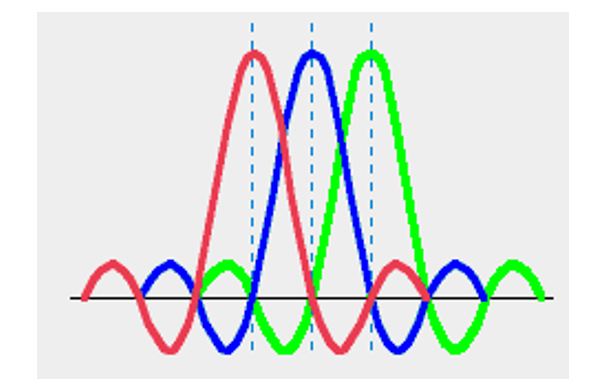
Figura N°9 Ortogonalidad entre funciones Sinc -- Fuente

De esta forma cada señal esta modulada en frecuencias distintas pero están lo suficientemente “agrupadas” para optimizar el ancho de banda, y muy importante, no se interrumpen unas con otras.
A continuación se presenta un diagrama en el que se puede apreciar todo los procesos descritos en el texto:

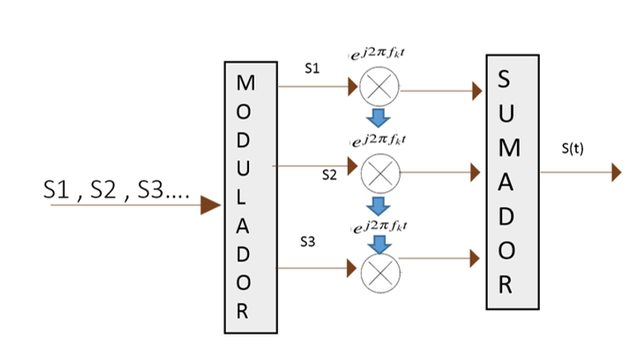
Figura N°10 Diagrama simple de un modulador OFDM – Elaboración Propia

Se ha podido describir los aspectos fundamentales que rigen la tecnología de OFDM, en una próxima entrega será detallada a través de un modelo experimental la implementación de esta multiplexación en sistemas ópticos, lo cual es un paradigma relativamente nuevo y que está teniendo buenos resultados en la transmisión de información.

Referencias

Comunicaciones MIMO OFDM sobre Fibra Óptica; Trabajo Fin de Grado
Grado en Ingeniería de las Tecnologías de Telecomunicación; Virgilio Medel; Sevilla 2015

Diseño y simulación de sistemas OFDM / A ópticos para redes de nueva generación ; Trabajo Fin de Grado, Grado en Ingeniería de las Tecnologías de Telecomunicación; Rivas R, ; Caracas 2012

Pares clásicos de la transformada de Fourier