MODELADO DE UN SISTEMA DE COMUNICACIÓN ÓPTICO BASADO EN LA TECNOLOGÍA DE MULTIPLEXACIÓN POR DIVISIÓN DE FRECUENCIAS ORTOGONALES (OFDM)

Saludos estimados lectores !

En una entrega anterior, se detalló el funcionamiento de la Multiplexación por División de Frecuencias Ortogonales (OFDM) siendo esta una técnica perteneciente al dominio de las comunicaciones digitales la cual presenta grandes rendimientos en la trasmisión de información, específicamente por su gran robustez ante la interferencia intersimbolica (ISI); a pesar de que OFDM fue diseñada en principio para operar con medios de transmisión “no guiados” o inalámbricos , esta modulación está teniendo un auge bastante interesante a lo que respecta su implementación en sistemas guiados como es el caso de la fibra óptica. Bien es sabido que la fibra óptica es el medio más potente de transmisión pues presenta anchos de banda sumamente elevados por tanto las tasas de bits que puede transmitir son muy altas, sin mencionar que las perdidas o desvanecimientos en la señal confinada suelen ser bastante despreciables, no obstante (y como se mencionaba en el artículo anterior) el flujo de aplicaciones en materia de Telecomunicaciones ha traído consigo una demanda cada vez mayor de la ingeniera que sostiene las comunicaciones a largas distancias; en medio de esta situación se platea la combinación de la tecnología OFDM con medios ópticos guiados (fibra óptica) ; a grandes rasgos, se puede argumentar que OFDM optimiza la capacidad espectral de un canal determinado gracias a su principio de ortogonalidad, se nota entonces el gran potencial que puede desarrollar si se intercepta con sistemas de comunicaciones ópticos, pues los anchos de banda serian mejor utilizados.

Claro está, para que ambos principios converjan exitosamente deben ser considerados aspectos técnicos importantes, además de las debidas adecuaciones que se han de realizar.

Fuente

La finalidad de este texto es proporcionar y detallar el modelaje de un sistema de comunicaciones basado en OFDM definido dentro de un canal óptico, para ello se ha seleccionado el diagrama propuesto por Medel (2015) en donde se ilustra claramente el funcionamiento modular del aparataje de comunicaciones con las propiedades mencionadas previamente.

A continuación se muestra el diagrama del sistema desde el origen de los datos en transmisión hasta el extremo de recepción:

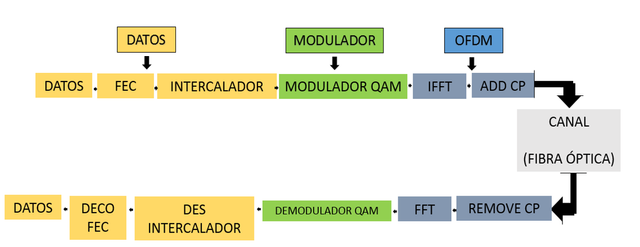
Figura N°1 Diagrama de un sistema Óptico basado en OFDM – Fuente Medel (2015) ; adaptado por Abiad (2018)

A lo largo de este diagrama se perciben distintos módulos que cumplen funciones específicas, lo práctico que resulta este diseño es el poder identificar las etapas que delimitan los distintos procesos por los que atraviesan las señales (datos) en la trayectoria transmisor-receptor.

Se identifican entonces los pilares de este sistema:

1. Bloques de datos (bits): comprenden el flujo de 0s y 1s que manejan las etapas de trasmisión y recepción.
2. Modulador/Demodulador QAM: básicamente se definen como los circuitos electrónicos encargados de modular/desmodular este flujo de datos , empleando la Modulación por Amplitud de Cuadratura (QAM) trasformando los bits en símbolos QAM; el número de constelaciones (agrupación de bits) varían según la modulación aplicada, la cual puede ser 32QAM, 64QAM, 128QAM , etc.
3. Etapa OFDM: en concreto, capta los símbolos QAM para su posterior inclusión en las ondas portadoras OFDM, estas señales son pasadas al dominio temporal en donde se le anexara a cada símbolo el intervalo de guarda correspondiente.
4. Canal: el medio de transporte como se sabe será la fibra óptica.
   Se procede a detallar el funcionamiento de la etapa de transmisión compuesta por los bloques de datos, símbolos QAM y símbolos OFDM:

Figura N°2 Etapa de Transmisión – Fuente Medel (2015) ; adaptado por Abiad (2018)

En primera instancia se requiere una fuente de generación aleatoria de bits, lo cual representa la información que será codificada con respecto a las condiciones propias del canal, este primer apartado se relaciona mucho con el siguiente, pues las implicaciones dadas para que un bloque de datos sea más o menos complejo (en tamaño) está directamente relacionado con las técnicas de detección y corrección de errores, en este caso se emplea FEC (Corrección de errores hacia adelante), es decir un bloque de datos será más grande si se decide emplear más bits de redundancia para que la información este mejor protegida. Para el caso analizado, se emplea codificación FEC , específicamente LDPC (Low Density Parity Check) el cual es un código lineal en el que se tiene una matriz de baja paridad lo que significa que tiene pocos elementos distintos de cero , lo cual representa además, el poder comunicar de forma eficaz a través de un canal relativamente ruidoso una gran tasa de bits.

Seguidamente los bits que son procesados por el FEC se combinan con el intercalador de manera que el resultado de esta operación traiga consigo una disposición aleatoria de la cadena de bits tratada, esto resulta útil en los sistemas digitales pues es muy frecuente que un 1 o un 0 se detecte de forma errónea en recepción, por tanto la aleatoriedad garantiza que si un bit tuvo problemas, este no afecte a la tira total de bits. Una vez los elementos binarios sean tratados por el intercalador estos se dirigen a la entrada del modulador QAM, en esta instancia los bits son agrupan en “símbolos” los cuales tendrán definidos una forma de onda específica para su posterior transporte en el complejo de comunicación; es de destacar que en la trayectoria del sistema no se envían directamente los bits, pues esto supondría fluctuaciones de voltajes que imposibilitarían la transición, en este caso se emplea la modulación en cuadratura en donde la información transmitida está contenida en la fase y amplitud de la señal.

Hasta ahora no se ha hecho más que describir el funcionamiento de un sistema digital genérico, en adelante se dedicara algo más de rigor para especificar los pormenores que surgen cuando OFDM entra en juego.
Una vez se construyan los símbolos QAM estos entraran al bloque de OFDM, donde serán “montados” sobre las portadoras (OFDM); esta sección corresponde a una de las más críticas pues como se puede apreciar en el diagrama original, este conjunto de bloques (IFFT, ADD CP) son la antesala para la transmisión hacia al medio de la fibra.

Consideraciones:
En el presente estudio, se plantean dos modelados para describir el funcionamiento del canal, AWGN ( Additive White Gaussian Noise) y MIMO ( Multiple-input Multiple-output ), se aclara que la intensión no es profundizar de lleno en estas concepciones, sino mas bien a través de nociones básicas de estos dos modelos poder entender lo que sucede con la señal OFDM conforme se avanza en el diseño propuesto. Se analiza de forma paralela AWGN y MIMO:

Análisis del modelo AWGN

Se interpreta de forma intuitiva el funcionamiento de los bloques IFFT y ADD CP cuando se considera el modelo de AWGN, pues lo que ocurre es una distribución los símbolos QAM con el equivalente de portadoras OFDM , estas últimas pueden estar dispuestas en gran cantidad pero no todas serán utilizadas para el envío de estos nuevos símbolos creados, la siguiente imagen ilustra lo que se ha dicho:

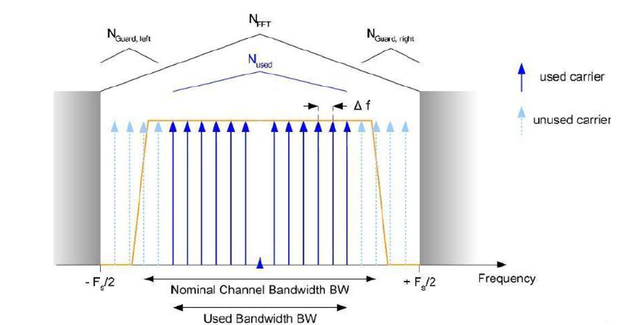Figura N°3 Símbolos QAM montados en portadoras OFDM – Fuente Medel (2015)

Ahora bien, los “pulsos” OFDM han sido debidamente compuestos, por tanto el siguiente paso será añadir el intervalo de guarda (este proceso de fue descrito en detalle en una entrega anterior) , pero las señales, como se puede apreciar en la figura, nos muestran una lectura frecuencial, razón por la cual se aplica una Transformada Rápida de Fourier Inversa (IFFT) y así pasar al dominio del tiempo en donde el bloque ADD CP (valga la redundancia) anexara este intervalo o prefijo cíclico. A la salida de este último bloque se tendría algo como:

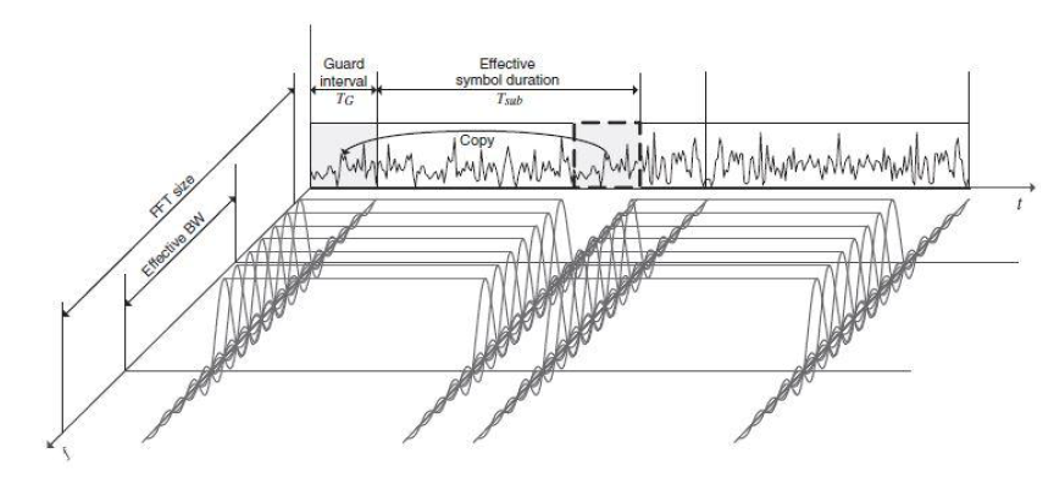Figura N°4 Símbolos OFDM en el Dominio Temporal y Frecuencial – Fuente Medel (2015)

Análisis del modelo MIMO
En contraste con el proceso anterior, en el modelaje MIMO solo se trabaja en el dominio de la Frecuencia, por tanto se verá simplificado el diagrama del sistema pues la inclusión de un prefijo cíclico no será necesaria, por su parte, la señal resultante en la etapa de transmisión debe ser multiplicada por una matriz que represente el comportamiento del canal, finalmente y sin más detalles, la señal puede ser enviada al canal.

Modelado del Canal

Definido los procesos inmersos en la etapa de transición, se procede a explicar lo propio visto en la etapa de recepción; de igual manera se analiza en paralelo lo concerniente a la aplicación de OFDM y modelaje del canal tanto en AWGN como en MIMO:

Se abordan los efectos producidos en la fibra, comenzando por develar el concepto de Dispersión por Modo de Polarización (PMD), básicamente es un fenómeno que afecta a la fibra cuando maneja transmisiones de altas tasas de velocidad , por lo general mayores a 10Gbps; el PMD tiene su origen en los defectos intrínsecos del material de la fibra, el problema radica en que el núcleo no logra adoptar una forma geométrica ideal, en este caso no logra ser lo suficientemente redondo traduciéndose en la generación de una alta dispersión que corrompe a la señal en su trayecto (laser) al receptor; el recorrido de la luz esta polarizado en dos ejes, estos a su vez forman un ángulo recto, si la fibra fuera “perfecta” ambas velocidades se propagarían en fase, no obstante en un sistema real cualquier imperfección produce el debido retraso en una de estas velocidades. Estas imperfecciones físicas conllevan a que existan índices de refracción variados, para una comprensión más formal, remítase al estudio de “birrefringencia”.

Figura N°5 Vistas Transversales de una fibra con efecto de birrefrigencia—Fuente

Como se especificaba anteriormente, el modo de propagación de la señal en la fibra esta caracterizado por una polarización en un eje vertical y horizontal respectivamente, por tanto si los índices de refracción “n” difieren existirán componentes de la señal original viajando a distintas velocidades, afectando así la comunicación. Es conocido como “Retardo Diferencial de Grupo” DGD a la diferencia de los retardos en polarización horizontal y vertical. Estas variaciones en los índices suponen retardo, el DGD es una magnitud medida en picosegundos.

Para modelar el comportamiento del campo eléctrico de una fibra, se hace uso de los “Vectores de Jones” , así la fibra puede plasmarse en un equivalente de su función de transferencia con elementos directamente relacionados, como la frecuencia y DGD.

Se muestra a continuación imágenes que distinguen entre materiales de fibra ideales y no ideales:

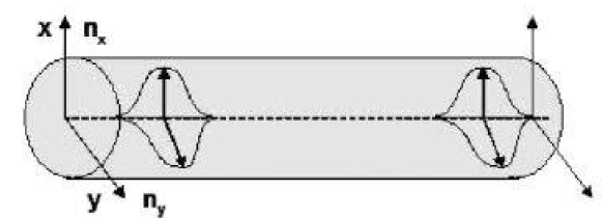
Figura N°6 Ejemplo de una fibra sin birrefringencia – Fuente Medel (2015)

En este caso la pureza del material hace que no existan desfases entre las velocidades, pues los índices de refracción “n” son equivalentes para ambos casos.
Situación contraria es la que se aprecia en la siguiente figura en donde los índices difieren. :

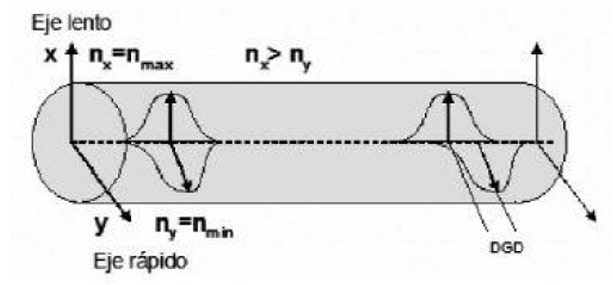
Figura N°7 Ejemplo de una fibra con birrefringencia – Fuente Medel (2015)

Si se consideran los cortes transversales de cada caso se tendría:

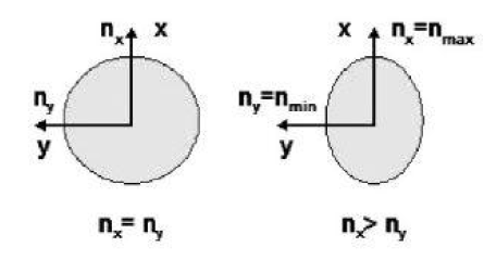
Figura N°8 Comparación transversal de fibras birrefrigente y no birrefrigente – Fuente Medel (2015)

Para comenzar a modelar el comportamiento del canal se presenta la función de transferencia:

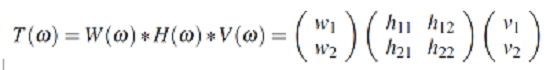
Cada elemento está representado por una matriz, W(w) y V(w) se expresan como las matrices de polarización de luz. Al no saber con certeza cómo será el comportamiento de la luz en el canal, se promueve la necesidad de usar un sistema que simule la “aleatoriedad” de los haces luminosos, por lo que se adopta el uso del sistema esférico de Poincaré el cual es un método muy utilizado para emular los comportamientos lumínicos. El sistema de coordenadas que contempla esta esfera, se homologa a un estado posible la polarización. Formalmente:

“Cada punto de la esfera de longitud 2φ y latitud 2w representa un estado de polarización, cuya elipse tiene un azimut φ y una elipticidad w.” Medel (2015).

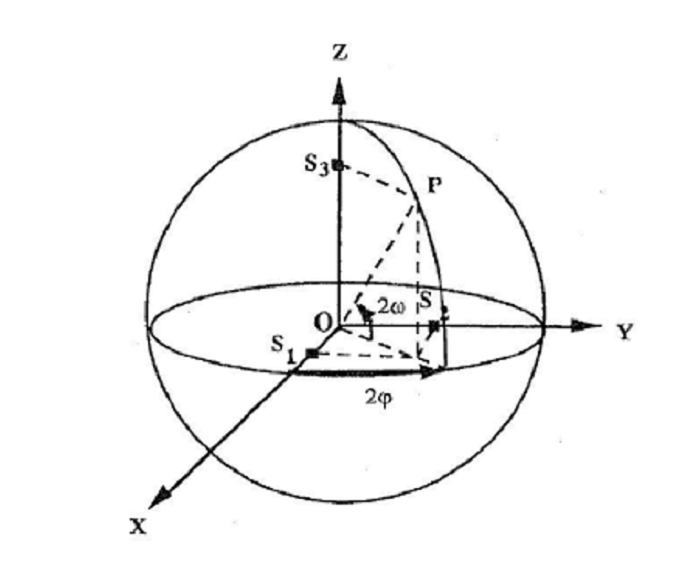
Figura N°9 Esfera de Poincaré – Fuente Medel (2015)

Como se trabaja en un sistemas de coordenadas esférico, cada punto está definido por tres componentes vectoriales, (r, φ, w), para el caso que interesa, se requiere trabajar con lo que se denomina polarización total, por tanto se normaliza un radio (r) a 1 , es decir el accionar estará ejerciéndose en la superficie esférica.
Lo siguiente que se debe hacer es especificar las ecuaciones que definen el estado de polarización de una onda electromagnética, en este caso, se realiza una interpretación del teorema de Stokes dando como resultado las siguientes expresiones:

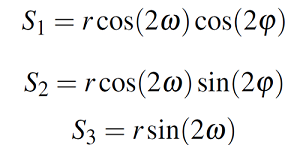
Los cálculos que siguen a continuación serán analizados desde un punto de vista más conservador, pues no se pretende desarrollar a plenitud los artificios matemáticos, sino que se interpretaran los resultados de dichas operaciones.
El sistema de coordenadas esférico que se ha definido con respecto a sus expresiones en el dominio de Stokes , debe ser llevado al espacio que se ha decidido utilizar para modelar la función de transferencia antes mencionada, en este caso se emplea la matriz de polarización de Jones. Para realizar las adecuaciones de las dimensiones, es de vital importancia considerar un ángulo arbitrario de rotación en el espacio de Stokes el cual se ha denominado “α”.
Así mismo, estos cambios dimensionales implican el uso de las matrices de Pauli:

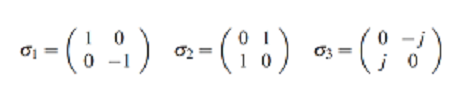
Finalmente, la expresión que establece la equivalencia del espacio de Stokes en el dominio de Jones se presenta a continuación:

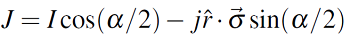
Consideraciones de la ecuación de Jones

El termino I, representa una matriz de identidad 2x2; la clave de estas deducciones es la convergencia de los vectores Jones y Stokes, la simbiosis existentes entre estas dos dimensiones es que uno de los vectores de Jones se representa como un “autovector” entre el vector columna y el vector unitario. La función vectorial se plasma como:

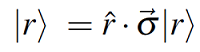
El vector que se ilustra en este formula es el vector de Pauli y sus componentes se definen como :

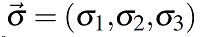
Entonces , al multiplicar el vector matricial de Stokes y el vector de Pauli se obtiene :

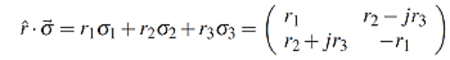
Ahora que se han realizado las operaciones preliminares que se presentaban en la ecuación de Stokes-Jones , se obtiene la matriz polarización lumínica. Para lograr cubrir el análisis de este modelo, se emplean dos matrices, una a cada extremo del material (fibra) , denominadas W y V respectivamente.
Las propiedades matriciales de cada una de estas funciones son que su determinante es igual a 1 , además si se efectúa el producto de la matriz polarizada con el equivalente de la matriz hermética se obtendrá la matriz identidad :

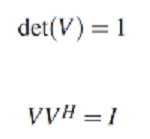
De la función de transferencia planteada en un principio, se han definido todas las matrices que están en juego, solo falta por modelar la matriz H , cabe destacar que será esta la que contenga la dispersión polarizada por tanto es la responsable del efecto tabulado como DGD, siendo afectada directamente por la frecuencia; para cada una de las portadoras existirán comportamientos diferentes, pues la señal OFDM para cada canal variara debido a los retardos por birrefringencia como se explicó anteriormente. La matriz H queda expresada como :

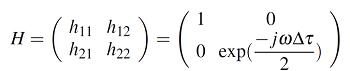
La interpretación que se puede hacer de que los elementos h12 y h21 sean 0 es que los canales están desacoplados , el elemento h11 se define como 1 para que el sistema sea “causal” y por ultimo h22 esta asumido como la dispersión del pulso.
Lo que resta seria calcular el producto de todas las matrices que integran la función de transferencia, por tanto la señal de salida será el producto de la señal de entrada y la función de transferencia propiamente dicha:

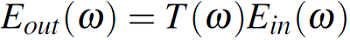
Ahora que se ha modelado el canal y la señal entra en la etapa de recepción, se procede a explicar cómo se recupera la información a partir de los símbolos recibidos:

Figura N°10 Etapa de Recepción – Fuente Medel (2015) adaptado por Abiad (2018)

Primeramente la señal está implicada en el dominio temporal por lo que se ha de depurar el intervalo de guarda que fue añadido en la etapa de transmisión , para ello se utiliza el bloque REMOVE CP , a la salida de este bloque se logra obtener la señal OFDM pura , la precisión del REMOVE es muy importante pues este dispositivo debe estar lo debidamente calibrado para depurar la magnitud temporal de la señal que fue anexada como prefijo cíclico; paso a seguir será llevar a la señal al dominio frecuencial , lo cual es efectuado por el bloque FFT cuya acción no es más que aplicar la transformada de Fourier a la señal recibida.

A la salida de la sección de los bloques OFDM, la señal es recibida por el demodulador QAM , este bloque captara símbolos cuyas componentes están definidas en frecuencia, por lo que cabe la posibilidad de que contenga un nivel de ruido considerable, al igual que los dispositivos anteriores, el equipo debe ser lo suficientemente eficaz para poder “seleccionar” de forma apropiada (mediante la consideración de reglas log likelihood ratios LLR) los bits que integran la totalidad de símbolos, es decir, esto involucra un procedimiento inverso a lo que ocurre en el modulador. Como se definió , la técnica de decisión probabilística será LLR, pues bien, el mecanismo que será empleado para la decodificación como tal de los bits será : Max log MAP, su funcionamiento es el siguiente:

“Como es bien sabido, en el sistema de codificación del transmisor, los bits codificados son agrupadas en vectores de bits, cada uno con la longitud k = log2M y denotado por b = (b0b1:::bk􀀀1). El vector b se asigna a continuación a un punto de la constelación x 2 c para la transmisión, en donde c = fxm;0 _ m < 2kg denota el conjunto de señales de tamaño 2k, también conocido como alfabeto.” Madel (2015)

En síntesis, este algoritmo lo que permite es establecer (dadas las condiciones iniciales del sistema) el conjunto de palabras que serán válidas a la hora de su respectiva recepción.

Pasado el proceso de demodulación, ahora los símbolos son dispuestos en el bloque del desintercalador , en donde básicamente se restablece el orden original de la cadena que un principio se acomodó de forma aleatoria , para poder lógralo este dispositivo deberá contener la semilla que se aplicó en el algoritmo de aleatoriedad, sin más que agregar en este apartado, los símbolos LLR acceden al decodificador FEC donde ; por medio de los códigos lineales LPDC se recuperan los bits (1s , 0s), este equipo realizara los calculo probabilísticos para cada bit y de existir algún error en este punto, se procede con la corrección del mismo.
A fin de cuentas, a la salida de este último bloque tendremos un formato de datos binario el cual será recibido por el Rx, este último apartado suele ser denominado como “sumidero”.

Se ha podido describir el proceso que conlleva la implementación de OFDM en un canal óptico, además de tildar aspectos generales pertenecientes a la comunicación digital, estos esquemas de corridas en frio ilustran el comportamiento de sistemas reales que operaran en los distintos paradigmas de la transmisión de datos, específicamente en la tecnología que se ha estudiado .

Referencias

Comunicaciones MIMO OFDM sobre Fibra Óptica; Trabajo Fin de Grado; Grado en Ingeniería de las Tecnologías de Telecomunicación; Virgilio Medel; Sevilla 2015

Diseño y simulación de sistemas OFDM / A ópticos para redes de nueva generación ; Trabajo Fin de Grado, Grado en Ingeniería de las Tecnologías de Telecomunicación; Rivas R, ; Caracas 2012

TÉCNICAS EN COMUNICACIONES DIGITALES – MULTIPLEXACIÓN POR DIVISIÓN DE FRECUENCIAS ORTOGONALES (OFDM) ; Abiad (2018)

Diseño y simulación de sistemas OFDM / A ópticos para redes de nueva generación ; centro tecnológico de telecomunicaciones de Catalunya ; Dr. Josep M. Fabrega Sánchez

Fundamentos de La Polarización y sus Tipos