Angulo sólido subtendido por una placa rectangular con respecto a un punto situado directamente sobre uno de sus vértices
Saludos para toda la comunidad de Steemit, especialmente la comunidad relacionada con el proyecto @steemstem y @stem-espanol. Saludos mis muy queridos y atentos Steemians-Lectores. En esta oportunidad les muestro, mediante una presentación bien detallada y didáctica, la forma de calcular el Angulo Sólido subtendido por una placa rectangular con respecto a un punto situado directamente sobre uno de sus vértices. Todo esto lo hago, como es mi costumbre, con la finalidad de hacer más fácil de entender todos los procedimientos involucrados.
Para tener una excelente comprensión del material presentado en este post, les recomiendo leer previamente mis posts:
- EL ANGULO SOLIDO - PARTE 1 - CONOCIMIENTOS BASICOS.
- EL ANGULO SOLIDO - PARTE 2 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 3 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 4 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 5 - DEFINICION DE ANGULO SOLIDO.
- EL ANGULO SOLIDO - PARTE 6 - EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO.
- EL ANGULO SOLIDO - PARTE 7 - PROPIEDADES DEL ANGULO SOLIDO.
- ANGULO SOLIDO SUBTENDIDO POR UNA DE LAS CARAS DE UN CUBO CON RESPECTO A UN PUNTO SITUADO EN EL CENTRO DEL MISMO
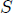 y dimensiones
y dimensiones 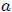 ,
, 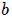 .
.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
Mis muy estimados Steemians-Lectores, esta vez deseamos calcular el Angulo Sólido 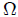 subtendido por una placa rectangular, de superficie
subtendido por una placa rectangular, de superficie 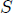 y dimensiones
y dimensiones 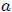 y
y 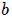 , con respecto a un punto
, con respecto a un punto 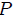 situado directamente sobre uno de sus vértices a una altura
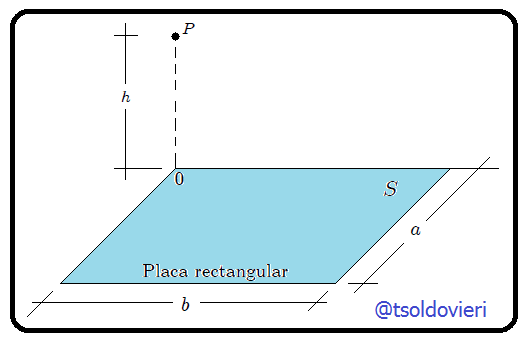
situado directamente sobre uno de sus vértices a una altura 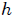 . En la figura 1 les muestro gráficamente lo que he dicho anteriormente. El cálculo se los presentaré mediante dos procedimientos distintos, utilizando coordenadas Cartesianas.
. En la figura 1 les muestro gráficamente lo que he dicho anteriormente. El cálculo se los presentaré mediante dos procedimientos distintos, utilizando coordenadas Cartesianas.
PROCEDIMIENTO 1:
Para llevar a cabo la anterior tarea, mis Steemians-Lectores, emplearé un sistema de coordenadas Cartesianas con el origen posicionado en el vértice que está directamente debajo de 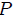 , como les muestro en la figura 2.
, como les muestro en la figura 2.
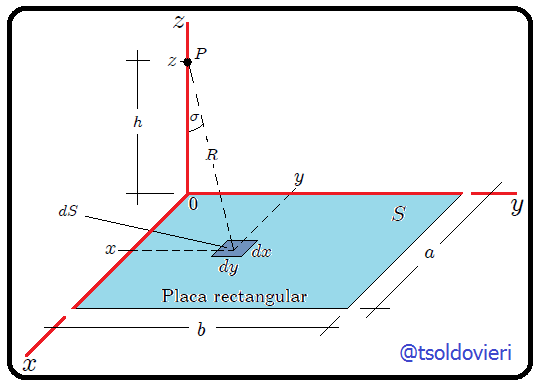
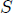 con respecto al punto
con respecto al punto 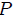 , posicioné un sistema de coordenadas Cartesianas de manera que su origen coincida con el vértice que está justo debajo de dicho punto.
, posicioné un sistema de coordenadas Cartesianas de manera que su origen coincida con el vértice que está justo debajo de dicho punto.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
En la figura antes señalada podemos observar que he dibujado una superficie diferencial 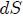 que está sobre la superficie plana
que está sobre la superficie plana 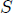 . En coordenadas Cartesianas podemos escribir que,
. En coordenadas Cartesianas podemos escribir que,
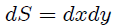
Ahora bien, a partir de la definición de Angulo Sólido (5) dada en el post EL ANGULO SOLIDO - PARTE 6 - EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO, tenemos que el Angulo Sólido diferencial 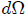 subtendido por la superficie diferencial
subtendido por la superficie diferencial 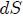 con respecto al punto
con respecto al punto 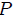 viene dado por,
viene dado por,
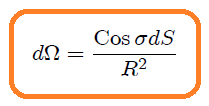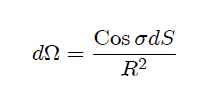
o si sustituimos aquí (1),
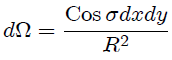
pero de la figura 2 es fácil que determinemos que,
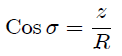
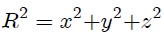
entonces al sustituir estas expresiones en (3) nos resulta,
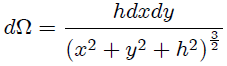
donde he tenido presente que 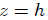 . Si ahora integramos esta última expresión obtenemos,
. Si ahora integramos esta última expresión obtenemos,
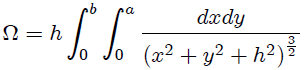
Estimados Steemians-Lectores, si integramos primero con respecto a 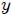 , utilizando 1.2.43.-17 (página 92, escrita para
, utilizando 1.2.43.-17 (página 92, escrita para 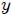 ) de la referencia (3),
) de la referencia (3),
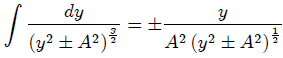
con 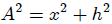 nos resulta de forma muy sencilla,
nos resulta de forma muy sencilla,
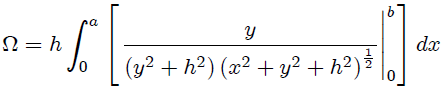
de donde,
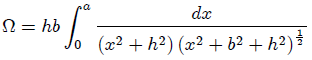
Si ahora, mis atentos Steemians-Lectores, empleamos 1.2.45-10 (página 94) de la referencia 3,
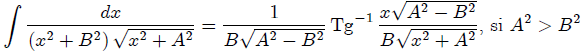
con 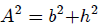 y
y 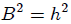 (notemos que se cumple
(notemos que se cumple 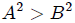 ) resulta,
) resulta,
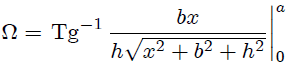
de donde finalmente,
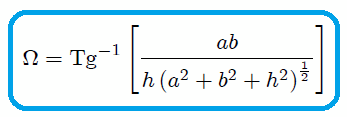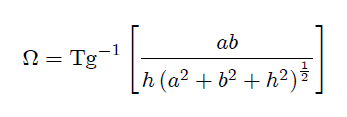
que es el Angulo Sólido buscado.
PROCEDIMIENTO 2:
Mis muy estimados Steemians-Lectores, el anterior cálculo lo pudimos haber llevado a cabo dividiendo el rectángulo en dos triángulos, como les muestro en la figura 3.
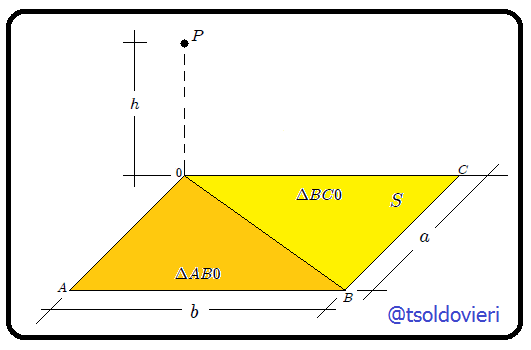
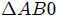 y
y 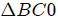 .
.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
En efecto,
Triángulo  :
:
Para este caso, según lo mostrado en la figura 4, podemos escribir que,
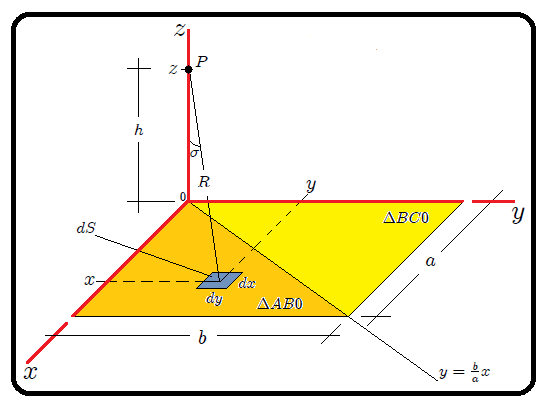
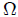 subtendido por la placa rectangular con respecto al punto
subtendido por la placa rectangular con respecto al punto 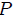 .
.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
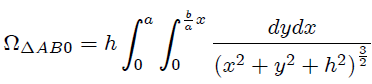
a partir de la cual, realizando la integración con respecto a 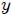 , obtenemos fácilmente la expresión,
, obtenemos fácilmente la expresión,
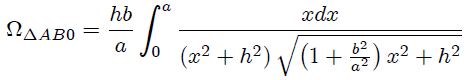
donde he utilizado (8) con 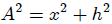 . Si en esta integral le hacemos el cambio de variable,
. Si en esta integral le hacemos el cambio de variable,
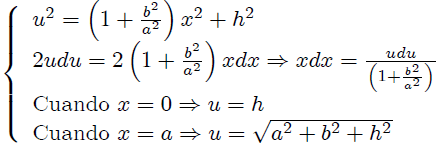
nos resulta que,
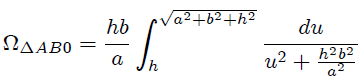
Si empleamos 1.2.10.-14 (página 41, escrita para 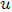 ) de la referencia 3,
) de la referencia 3,
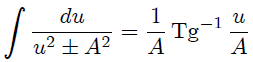
con 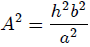 para integrar (17), obtenemos que,
para integrar (17), obtenemos que,
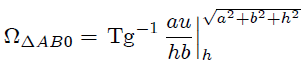
de donde, al devolver el cambio de variable,
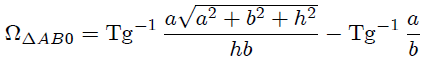
Ahora Steemians-Lectores, al utilizar 4.4.34. (página 80) de la referencia 7,
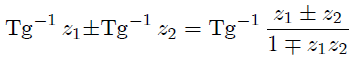
con,
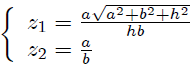
nos resulta,
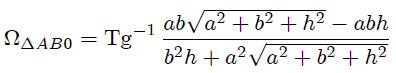
Triángulo 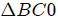 :
:
Para este caso, según lo mostrado en la figura 4, podemos escribir que,
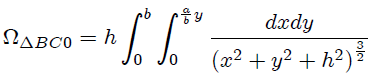
a partir de la cual, mediante un procedimiento análogo al seguido para el cálculo de 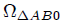 , obtenemos el resultado,
, obtenemos el resultado,
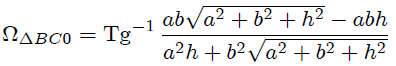
Notemos mis estimados Steemians-Lectores que 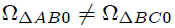 , contrario a lo que se podría haber pensado de antemano. Esto es debido a que , contrario a lo que se podría haber pensado de antemano. Esto es debido a que 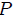 está sobre un vértice que es distinto en cada triángulo. Si la placa fuese cuadrada, es decir está sobre un vértice que es distinto en cada triángulo. Si la placa fuese cuadrada, es decir 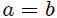 , entonces ambos ángulos sólidos resultan idénticos. , entonces ambos ángulos sólidos resultan idénticos. |
|---|
El Angulo Sólido 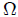 subtendido por la placa rectangular con respecto a
subtendido por la placa rectangular con respecto a 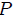 vendrá dado por,
vendrá dado por,
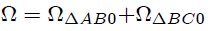
que en vista de (23) y (25) nos resulta en,
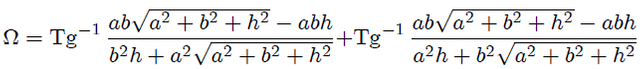
Si utilizamos aquí (21) con,
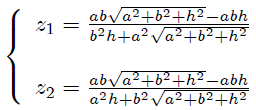
obtenemos finalmente que,
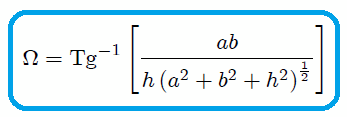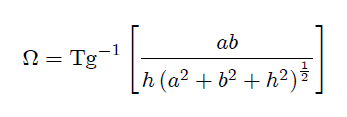
resultado idéntico al (13), como era de esperarse.
Mis muy estimados Steemians-Lectores, les dejo como tarea llevar a cabo el anterior cálculo usando coordenadas cilíndricas y coordenadas esféricas, verificando que el resultado sigue siendo el mismo. |
|---|

BIBLIOGRAFIA CONSULTADA Y RECOMENDADA
Aquí les presento, mis Steemians-Lectores, 8 textos que consulté para la elaboración del presente post. Indico las páginas consultadas.
Soldovieri C., T. & Viloria A., T. EL ANGULO SOLIDO Y ALGUNAS DE SUS APLICACIONES. Preprint, 2018. Página 77.
Tipler, P. A. & Mosca, G. PHYSICS FOR SCIENTISTS AND ENGINEERS. W. H. Freeman and Company, 6th edition, 2008. Página 753.
Prudnikov, A. P.; Brychkov, Y. A. & Marichev, O. I. INTEGRALS AND SERIES: ELEMENTARY FUNCTIONS, volume 1. Taylor & Francis, 1998. Páginas 92 y 94.
Faget, J. & Mazzaschi, J. TEMAS PROGRAMADOS DE FISICA - GENERALIDADES, volume 1. Editorial Reverté, S.A., 1976. pp. 121 - 135. Página 123.
Kaufman, A. A. GEOPHYSICAL FIELD THEORY AND METHOD - GRAVITATIONAL, ELECTRIC AND MAGNETIC FIELDS, volume A. Academic Press, INC., 1992. Páginas 12 - 22.
Eyges, L. THE CLASSICAL ELECTROMAGNETIC FIELDS. Dover Publications, 1972. Páginas 12 - 22.
Abramowitz, M. & Stegun, I. A. HANDBOOK OF MATHEMATICAL FUNCTIONS. Dover Publications, New York, 10th edition, 1972. Página 80.
Alonso, M. & Finn, E. J. FISICA - MECANICA, volume 1. Fondo Educativo Interamericano, S.A., 1970. Página 22.


Estimados amigos Steemians-Lectores. Espero que la anterior información les sea de mucha utilidad. Como ya es costumbre, si tienen preguntas no duden en hacérmelas llegar pues, con mucho gusto, les atenderé. Igualmente, si tienen detalles que puedan nutrir o mejorar la anterior información, por favor, háganmelas saber. Hasta mi próximo post ¡Saludos a todos! 😁.
Si deseas leer más artículos científicos de buena calidad, no pierda el tiempo, visite las etiquetas #steemstem y #stem-espanol. Es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete al canal de @steemstem. También puedes visitar el blog @steemstem y obtener mas información.


¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias @entropia, excelente labor la que realizan. Gracias por el continuo apoyo que brindan a nuestras publicaciones. Seguiré trabajado y apoyando su labor. Saludos cordiales.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for the support @steemstem. Regards.
Saludos @tsoldovieri, esta vez reconozco que no pude seguir tu disertacion, demasiada matematica ejejjejeje. Pero te felicito por semejante esfuerzo. Un post muy bien presentado y limpio como dicen los conocedores de steemit.
SALUTATIONS DU VENEZUELA
Amigo @soy-venezuelien, gracias por tu sincero comentario y por el apoyo que me brindas.
Lamento que no hayas podido seguir mi disertación, es verdad, hay bastante matemática involucrada jajajajaja. Saludos cordiales.
Saludos estimado @tsoldovieri. Sus trabajos y su didáctica son de primera. Es un placer contar con sus conocimientos y aportes. Mis felicitaciones.
Amigo y colega @lorenzor, gracias y es también para mí contar con los suyos. Saludos.
Como siempre amigo @tsoldovieri,nos presenta un excelente trabajo, muy didáctico. Felicitaciones!
Gracias amiga @ufv. Saludos.
Hola @tsoldovieri muy buen aporte el que presentas en tu publicación, donde se evidencia claramente la aplicación del saber matemático en un estudio concreto!! Adicionalmente celebro tu habilidad para crear las ilustraciones a partir de Paint!! Saludos fraternos!!
Gracias amiga @reinaseq por tu motivador comentario y por tu valioso apoyo. La habilidad con el Paint la he logrado con los años de experiencia al elaborar las ilustraciones de mis textos. Puedes ver y descargar los borradores desde mi web http://www.cmc.org.ve/tsweb Si lo deseas, podrías firmar el libro de visitas de la misma para dejar tus comentarios. El link está en la parte superior derecha de la página, al lado de la calavera que mueve el dedo. Gracias nuevamente. Mis saludos cordiales.
Buen post, profesor Terenzio. Bastante técnico. Saludos cordiales.
Gracias por tu comentario y apoyo amigo @eniolw. Saludos.
Congratulations @tsoldovieri! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Thanks!
Congratulations @tsoldovieri! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Thanks!
@tsoldovieri, thank you for supporting @steemitboard as a witness.
Click on the badge to view your Board of Honor.
Once again, thanks for your support!
Do not miss the last post from @steemitboard:
Thanks!