Hola amigos continuando con mis publicaciones referentes a las ciencias de la matematica y la fisica hoy quiero hacer referencia al Movimiento Armonico Simple , si bien en mecánica y física, el movimiento armónico simple es un tipo especial de movimiento periódico u oscilación en el que la fuerza de restauración es directamente proporcional al desplazamiento y actúa en la dirección opuesta a la del desplazamiento.

El movimiento armónico simple puede servir como un modelo matemático para una variedad de movimientos, como la oscilación de un resorte. Además, otros fenómenos se pueden aproximar mediante un movimiento armónico simple, que incluye el movimiento de un péndulo simple y la vibración molecular. El movimiento armónico simple se caracteriza por el movimiento de una masa en un resorte cuando está sujeto a la fuerza restauradora lineal elástica dada por la Ley de Hooke. El movimiento es sinusoidal en el tiempo y demuestra una sola frecuencia de resonancia. Para que el movimiento armónico simple sea un modelo preciso para un péndulo, la fuerza neta sobre el objeto al final del péndulo debe ser proporcional al desplazamiento. Esta es una buena aproximación cuando el ángulo del swing es pequeño.

El movimiento armónico simple proporciona una base para la caracterización de movimientos más complicados a través de las técnicas del análisis de Fourier. Por lo tanto, se puede definir simplemente como el movimiento periódico de un cuerpo a lo largo de una línea recta, de modo que la aceleración se dirige hacia el centro del movimiento y también es proporcional al desplazamiento desde ese punto.

Introducción

El movimiento de una partícula que se mueve a lo largo de una línea recta con una aceleración cuya dirección es siempre hacia un punto fijo en la línea y cuya magnitud es proporcional a la distancia desde el punto fijo se denomina movimiento armónico simple [SHM].

En el diagrama, se muestra un oscilador armónico simple, que consiste en un peso unido a un extremo de un resorte. El otro extremo del resorte está conectado a un soporte rígido como una pared. Si el sistema se deja en reposo en la posición de equilibrio, entonces no hay fuerza neta que actúe sobre la masa. Sin embargo, si la masa se desplaza desde la posición de equilibrio, la primavera ejerce una fuerza elástica de restauración que obedece a la ley de Hooke.

Matemáticamente, la fuerza restauradora F viene dada por

F = - KX ,

donde F es la fuerza elástica de recuperación ejercida por el resorte (en unidades SI: N), k es la constante de resorte (N · m-1), y x es el desplazamiento desde la posición de equilibrio (m).

Para cualquier oscilador armónico mecánico simple:

Cuando el sistema se desplaza de su posición de equilibrio, una fuerza restauradora que obedece la ley de Hooke tiende a restablecer el equilibrio del sistema.
Una vez que la masa se desplaza de su posición de equilibrio, experimenta una fuerza restauradora neta. Como resultado, acelera y comienza a regresar a la posición de equilibrio. Cuando la masa se mueve más cerca de la posición de equilibrio, la fuerza de restauración disminuye. En la posición de equilibrio, la fuerza de restauración neta se desvanece. Sin embargo, en x = 0, la masa tiene impulso debido a la aceleración que ha impartido la fuerza restauradora. Por lo tanto, la masa continúa más allá de la posición de equilibrio, comprimiendo el resorte. Una fuerza de restauración neta entonces la ralentiza hasta que su velocidad alcanza cero, con lo cual se acelera nuevamente a la posición de equilibrio.

Siempre que el sistema no tenga pérdida de energía, la masa continúa oscilando. Por lo tanto, el movimiento armónico simple es un tipo de movimiento periódico.

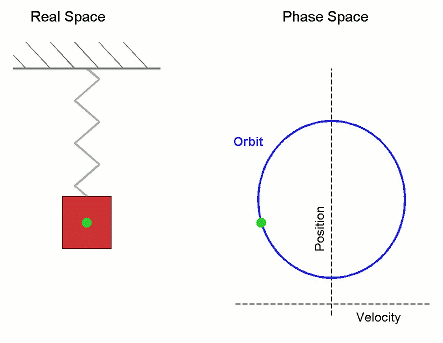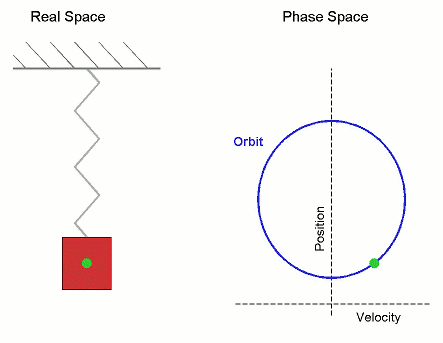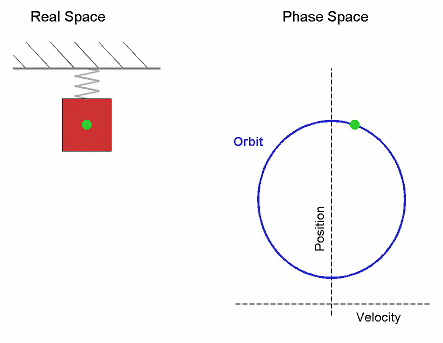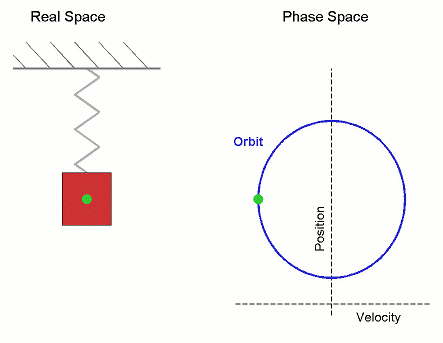
Fuente : Uso de imagen wikipedia :Movimiento armónico simple que se muestra tanto en el espacio real como en el espacio de fases. La órbita es periódica Aquí los ejes de velocidad y posición se han invertido de la convención estándar para alinear los dos diagrama

Dinámica

En la mecánica newtoniana, para el movimiento armónico simple unidimensional, la ecuación de movimiento, que es una ecuación diferencial ordinaria lineal de segundo orden con coeficientes constantes, puede obtenerse mediante la segunda ley de Newton y la ley de Hooke para una masa en un muelle.

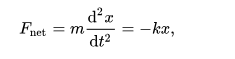
donde m es la masa inercial del cuerpo oscilante, x es su desplazamiento desde la posición de equilibrio (o media), y k es una constante (la constante de resorte para una masa en un muelle). (Tenga en cuenta que en realidad esto es de hecho una aproximación, solo válida para velocidades que son pequeñas en comparación con la velocidad de la luz).

Por lo tanto,

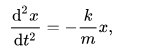
La solución de la ecuación diferencial anterior produce una solución que es una función sinusoidal.

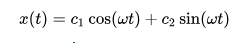
Esta ecuación se puede escribir en la forma:

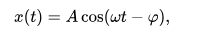
dónde

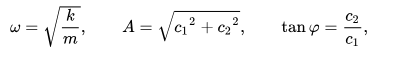
En la solución, c1 y c2 son dos constantes determinadas por las condiciones iniciales, y el origen se establece en la posición de equilibrio. [A] Cada una de estas constantes tiene un significado físico del movimiento: A es la amplitud (desplazamiento máximo desde la posición de equilibrio), ω = 2πf es la frecuencia angular, y φ es la fase. [B]

Utilizando las técnicas del cálculo, se puede encontrar la velocidad y la aceleración en función del tiempo:

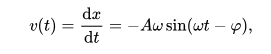
Velocidad:

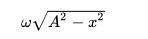
Velocidad máxima: {{{1}}} (en el punto de equilibrio)

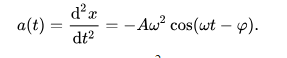
Aceleración máxima: Aω2 (en puntos extremos)

Por definición, si una masa m está por debajo de SHM, su aceleración es directamente proporcional al desplazamiento.

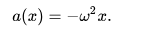
dónde

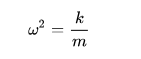
Dado que ω = 2πf,

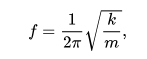
y, desde T = 1 / f
donde T es el período de tiempo,

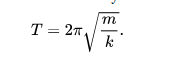
Estas ecuaciones demuestran que el movimiento armónico simple es isócrono (el período y la frecuencia son independientes de la amplitud y la fase inicial del movimiento).

Energía :

Sustituyendo ω2 con k / m
, la energía cinética K del sistema en el tiempo t es

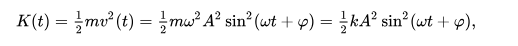
y la energía potencial es

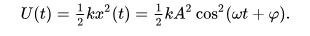
En ausencia de fricción y otras pérdidas de energía, la energía mecánica total tiene un valor constante

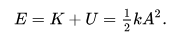
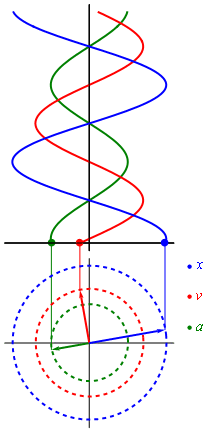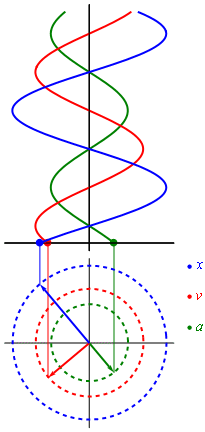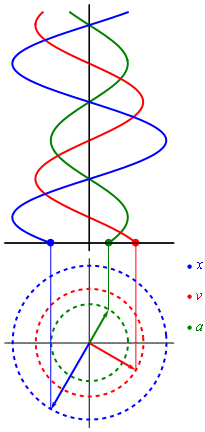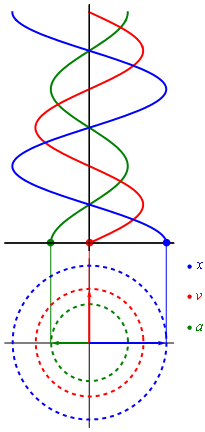
Fuente :Uso de imagen wikipedia :Evolucion en el tiempo de desplazamiento , donde la velocidad y la aceleracion hacen su movimiento

Ejemplos

Los siguientes sistemas físicos son algunos ejemplos de oscilador armónico simple.

Masa en un muelle

Una masa m unida a un resorte de resorte constante k presenta un movimiento armónico simple en un espacio cerrado. La ecuación para describir el período

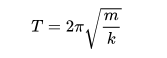
muestra que el período de oscilación es independiente tanto de la amplitud como de la aceleración gravitacional. La ecuación anterior también es válida en el caso en que se aplica una fuerza constante adicional sobre la masa, es decir, la fuerza constante adicional no puede cambiar el período de oscilación.

Movimiento circular uniforme

El movimiento armónico simple se puede considerar la proyección unidimensional del movimiento circular uniforme. Si un objeto se mueve con una velocidad angular ω alrededor de un círculo de radio r centrado en el origen del plano xy, entonces su movimiento a lo largo de cada coordenada es un movimiento armónico simple con amplitud r y frecuencia angular ω.

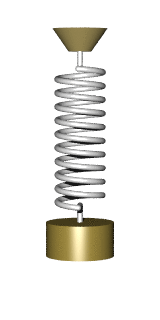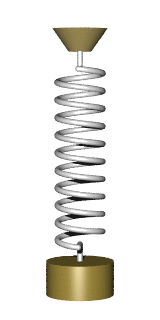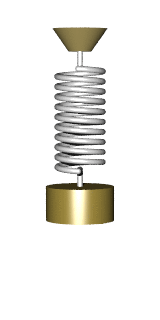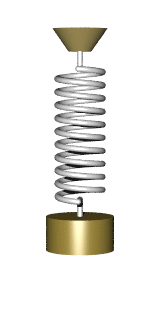
Fuente: Uso de imagen Wikipedia :Un sistema de masa de muelle no amortiguado experimenta un movimiento armónico simple.

Masa de un péndulo simple

En la aproximación de ángulo pequeño, el movimiento de un péndulo simple se aproxima mediante un movimiento armónico simple. El período de una masa unida a un péndulo de longitud l con aceleración gravitacional g viene dado por :

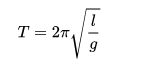
Esto muestra que el período de oscilación es independiente de la amplitud y la masa del péndulo, pero no de la aceleración debida a la gravedad, {\ displaystyle g} g, por lo tanto, un péndulo de la misma longitud en la Luna oscilaría más lentamente debido a la La fuerza del campo gravitatorio inferior de la Luna. Debido a que el valor de {\ displaystyle g} g varía ligeramente sobre la superficie de la tierra, el período de tiempo variará ligeramente de un lugar a otro y también variará con la altura sobre el nivel del mar.

Esta aproximación es precisa solo para ángulos pequeños debido a que la expresión de la aceleración angular α es proporcional al seno del ángulo de desplazamiento:

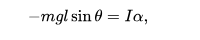
donde yo soy el momento de inercia. Cuando θ es pequeño, sin θ ≈ θ y, por lo tanto, la expresión se vuelve

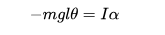
que hace que la aceleración angular sea directamente proporcional a θ, satisfaciendo la definición de movimiento armónico simple.

yugo escocés

Se puede usar un mecanismo de yugo escocés para convertir el movimiento rotativo y el movimiento alternativo lineal. El movimiento lineal puede tomar diversas formas dependiendo de la forma de la ranura, pero el yugo básico con una velocidad de rotación constante produce un movimiento lineal que es de forma armónica simple.

Fuente:Uso de imagen wikipedia :El movimiento de un péndulo no amortiguado se aproxima al movimiento armónico simple si el ángulo de oscilación es pequeño.

Si deseas leer contenido científico de calidad en habla hispana te invito a revisar la etiqueta #STEM-ESPANOL donde podrás encontrar diversidad de temas, Matemática, Física, Química, Biología, Medicina, entre otros.

Referencias :

• Walker, Jearl (2011). Principios de Física (novena edición). Hoboken, N.J.: Wiley.

• Thornton, Stephen T .; Marion, Jerry B. (2003). Dinámica clásica de partículas y sistemas (5ª ed.). Brooks Cole.

• John R Taylor (2005). Mecanica clasica. Libros de ciencia de la universidad.

• Grant R. Fowles; George L. Cassiday (2005). Analytical Mechanics (7ma ed.). Thomson Brooks / Cole.

• https://www.britannica.com/science/simple-harmonic-motion

• http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html