Verificación computacional de un modelo matemático para la función delta de Dirac utilizando Scilab
¡Hola estimados Steemians y miembros de la comunidad #stem-espanol!
Es un placer saludarles, mi nombre es Miguel Ángel Labrador soy estudiante de ingeniería electrónica de la Universidad Simón Bolívar, en Caracas, Venezuela. Desde hace un par de meses formo parte de la comunidad de Steemit, haciendo posts en su mayoría en inglés aunque, ahora que la comunidad de @steemSTEM se ha expandido hasta nuestro idioma, estoy muy entusiasmado de poder hablar y compartir con ustedes los temas que me gustan y me apasionan, en castellano.
En el presente artículo se presenta a la función delta de Dirac (o impulso unitario), llamada así en honor al físico Paul Dirac quien la introdujo por primera vez, así como el software Scilab como gran de apoyo para entender de qué va toda la historia sobre esta función o distribución, depende desde qué punto vista se la mire...¡Empecemos!
¿Y qué es Scilab?
Si estás leyendo este artículo tal vez hayas escuchado de Matlab, el cual es un poderoso lenguaje de programación de cálculo científico basado en matrices y vectores, su uso se ha extendido mucho en empresas y universidades desde hace varios años por su infinidad de aplicaciones en ciencias e ingeniería. Pues bien, si tampoco has oído hablar de él, te presento a SciLab, otro software de cálculo científico un poco menos conocido que, sin embargo, nada tiene que envidiarle a Matlab. Una de las diferencias entre Matlab y Scilab es que este último es un software open source o de código abierto por lo que es totalmente gratuito y está disponible para su descarga en su web oficial. Scilab tiene su propio lenguaje, aunque si estás familiarizado con Matlab u otros lenguajes de programación como C o C++, te resultará muy sencillo de manejar.
La función delta de Dirac
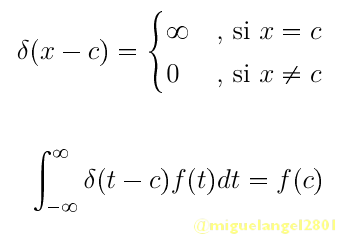
La función delta de Dirac o impulso unitario suele definirse de manera distinta en algunos libros de texto y en ocasiones algunas de estas definiciones son inconsistentes desde el punto de vista matemático, y la razón es que en matemáticas la delta Dirac no se considera una función pues no cumple con lo que se conoce como tal . La función impulso unitario, como la definen algunos autores (y el mismo Dirac en su momento), es aquella que satisface las expresiones de la figura 1. Aunque, esta definición no es consistente con la teoría de integración y nos lleva a incongruencias matemáticas. Sin embargo, no hay porque desanimarse ya que estrictamente hablando la función delta de Dirac no puede entenderse como una función convencional sino como una función generalizada, concepto que pertenece a la teoría de distribuciones del análisis matemático, aun así posee grandes aplicaciones en ciencias y en campos de la ingeniería como la teoría de control y en el procesamiento de señales. No obstante, no hay que restarle mérito a esta forma de describir al impulso unitario ya que nos da una aproximación intuitiva de lo que puede ser este objeto matemático.
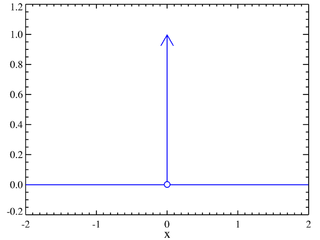

En resumen, para verificar que una secuencia de funciones converge al impulso unitario, esta debe cumplir al menos con ser:
- Absolutamente integrable
- Suave a trozos
- El área total bajo la curva debe ser 1
- Al actuar sobre otra función su resultado es dicha función evaluada en 0.
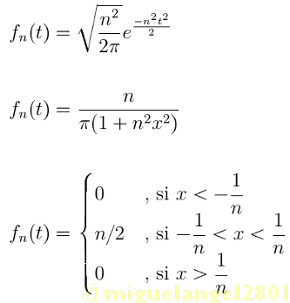
Bajo esta definición ya se pueden pensar en algunas funciones que podrían satisfacer el teorema. En la figura 4 se muestran algunas secuencias que, en el límite, convergen a la delta de Dirac. Se puede tomar la segunda, por ejemplo, para verificar que en efecto cumple con todas las condiciones para ser un modelo matemático de la función impulso unitario. Se hará la verificación utilizando Scilab.
A continuación se muestran, una encima de otra, las gráficas de la secuencia que hemos escogido para distintos valores de n.
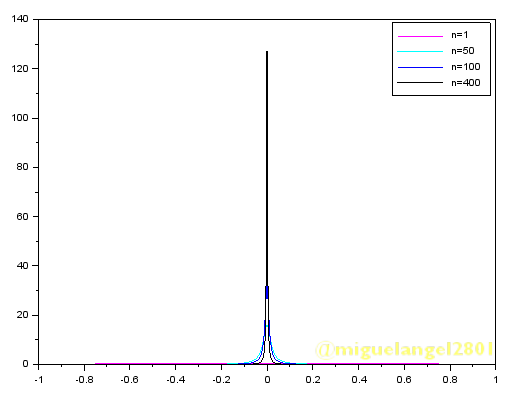
Figura 5: Secuencia para n=1, 50, 100, 400. Gráfica realizada en Scilab.
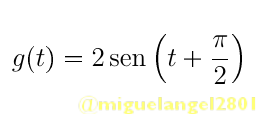
Aunque la gráfica es bastante parecido a lo que se esperaba, no diremos que la secuencia sirve como modelo solo por ello. Falta verificar que cumple con el teorema, en otras palabras, que al actuar sobre otra función cuando n tiende a infinito o, para fines prácticos, a un número 'grande', se obtengan los resultados esperados. Para esto se puede escribir el siguiente programan en Scilab, donde se define la función de prueba g(t), se generan las secuencias para los diferentes n y también la gráfica de la figura 5.
//Definimos una función que nos permita integrar /numericamente haciendo uso de rectángulos inscri/tos. El número de rectángulos es N.
function[result]=Integrate(t1,t2,N)
h=(t2-t1)/N
xk=t1
result=f(xk)*h
for k=2:N
xk=xk+h
result=result+f(xk)*h
end
endfunction
//Función de prueba, continua y definida en R.
function y=g(t)
y=2*sin(t+%pi/2)
endfunction
T=-1:0.001:1;
n=[1 50 100 400];
colour=['m' 'c' 'b' 'k'];
clf()
//Ciclo for para generar las cuatro secuencias, graficarlas y mostrar en pantalla los resultados para comparar la calidad de la aproximación.
for i=1:4
function y=secuencia(t)
y=n(i)*(%pi*(1+n(i)^2*t.^2)).^-1
endfunction
function y=f(t)
y=g(t)*secuencia(t)
endfunction
plot(T,secuencia(T),colour(i));
res=Integrate(-10,10,10000);
disp(res,'Para n = '+string(n(i))+':')
end
hl=legend(['n='+string(n(1));'n='+string(n(2));'n='+string(n(3));'n='+string(n(4))]);
//Fin del programa.
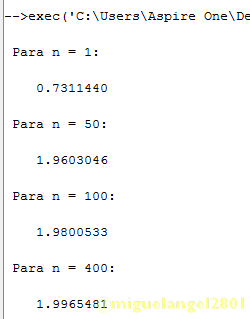
Tal como se muestra en la gráfica, al ejecutar el programa se generan curvas correspondientes a n=1, 5, 15, 50. Por otro lado también se muestra en pantalla los resultados de resolver numéricamente la integral del teorema para los valores de n mencionados ( véase la figura 7) . Se observa que a medida que se incrementa n (n tiende a un número más grande) la calidad de la aproximación es mayor. Téngase en cuenta que el resultado del teorema es la función de prueba evaluada en 0, en otras palabras, el resultado que se espera es g(0)=2, por lo que el programa respalda la tesis. La secuencia funciona como modelo matemático para la delta de Dirac.
Finalmente, a modo de comentario técnico, es posible dar valores más altos a n, sin embargo, esto puede comprometer la exactitud de los resultados si no se ajusta el número de rectángulos en la función Integrate. Al dar valores cada vez más grandes a n la mayor parte del área de la función se concentra en un intervalo más pequeño por lo que se necesitan más rectángulos (lo que se traduce en bases de rectángulo más pequeñas) para que el error sea lo más despreciable posible.
¿Tienes alguna pregunta? ¿Quieres compartir algo más sobre la delta de Dirac o Scilab? Déjame tus comentarios.
¡HASTA LA PRÓXIMA!
Referencias bibliográficas:
- Kamen E. and Heck B. (2008) Fundamentals of Signals and Systems using the Web and MATLAB (3rd edition). Pearson Education, Inc.
- Andrea S. y Mendoza A. (2001) Guía de Matemáticas VII. Departamento de Matemáticas Puras y Aplicadas, Universidad Simón Bolívar.
- González K. y Jahnke C. (1995) "La delta de Dirac como función". Revista Educación Matemática ISSN: 10188298.
Referencias en la Web
Scilab Wiki. Documentación de Scilab.
Enlace: https://wiki.scilab.org/Documentation
Imágenes
Figura 2-Gráfica ideal de la delta de Dirac
Crédito: PAR
Fuente
CC BY-SA 3.0Figura 3- Aproximación animada hecha en Matlab.
Crédito: Oleg Alexandrov
Fuente
Dominio públicoEl resto de las imágenes fueron creadas por mi a partir de Latex y/o editándolas con GIMP.
Nota: El programa realizado fue hecho en su totalidad por mi utilizando la versión 5.5.2 de Scilab.