Saludos estimados lectores espero se encuentren muy bien todos, esta vez les traigo la simulación de un tema bastante interesante como lo es la formación de las imágenes en los espejos y lentes abordado desde la óptica geométrica, mi artículo sobre este tema creo que fue muy bien recibido por ustedes quizás por ser objetos con los cuales estamos en contacto a diario, siempre nos vemos al espejo al vestirnos, al andar en el automóvil tenemos los espejos retrovisores y muchas personas usan lentes para corregir sus problemas visuales por lo cual resulta sumamente interesante saber cómo se forman las imágenes a través de estos objetos.
- Un rayo que incide paralelo al eje pasa por el foco y viceversa.
- Un rayo que pase por el centro de curvatura se regresa por el mismo camino pero en sentido inverso debido a que la incidencia es perpendicular.
Al trazar los rayos siguiendo las propiedades antes expuestas el lugar donde estos o sus prolongaciones convergen es decir se cortan, es donde se formará la imagen.
Recordemos además que todo espejo tiene:
- Radio de curvatura: es el radio de la esfera a la cual pertenece la superficie.
- Centro de curvatura: es el centro de la esfera a la cual pertenece nuestra superficie.
- Foco: es el punto sobre el eje donde convergen todos los rayos que inciden paralelos al eje.
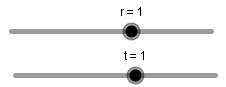
Conociendo estas propiedades y lo que conforma un espejo podemos empezar a crear nuestra simulacion, para esto empezaremos creando dos deslizadores; uno para el radio de curvatura del espejo y otro para el tiempo:
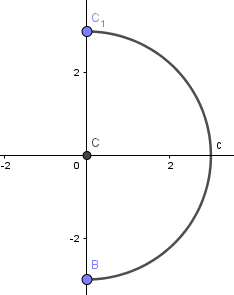
Luego de esto pasaremos a crear nuestro espejo, para esto iremos a la sexta ventana de la barra de herramientas y seleccionaremos la herramienta de arco de tres puntos con ella crearemos la forma de nuestro espejo, en este caso haré la superficie de un espejo cóncavo con su centro en el origen del plano:
Listo la superficie del espejo pasaremos a definir la posición del centro de curvatura y de los demás puntos que conforman el espejo pero primero cambiaremos la definición del centro colocando (r,0), luego cambiaremos la definición de los otros puntos del arco escribiendo en su definición:
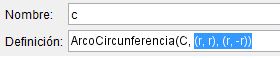
Solo deben cambiar la definición de los puntos que se encuentran en el lugar que aparece sombreado en la imagen de arriba, el punto "C" corresponde al centro de curvatura y su definición ya la modificamos antes, con esto logramos modificar el radio de curvatura a nuestro gusto:
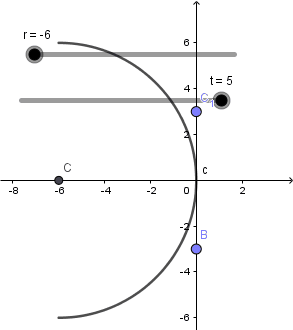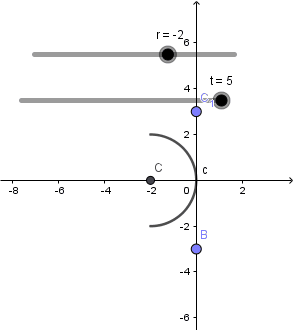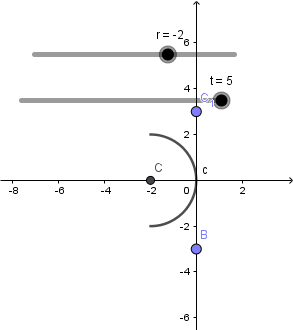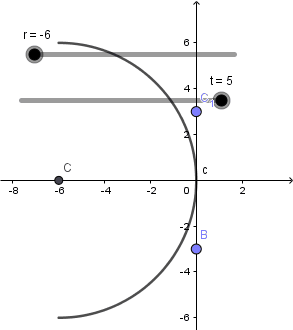
Hecho esto pasaremos a establecer el foco para ello crearemos un punto con definición (r/2,0) debido a que el foco se encuentra a una distancia de la mitad del radio, es decir entre el centro de curvatura y el vertice del espejo.
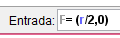
Al estar todo vinculado con el deslizador "r" logramos que todo se muevan en conjunto, manteniendo los valores correctos para las distancias de cada punto:
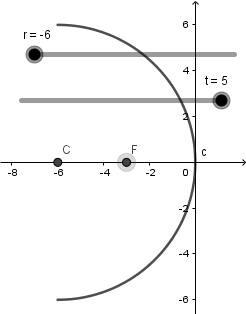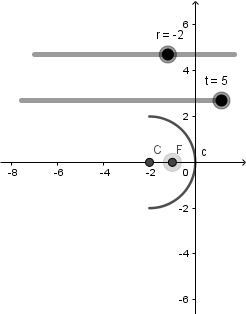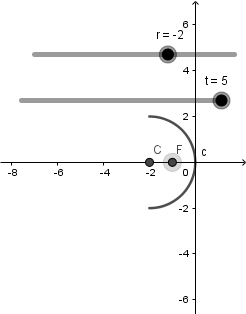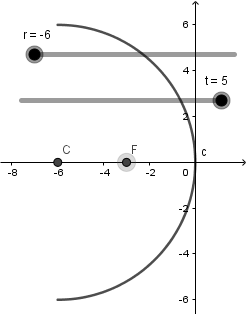
Hecho todo lo anterior pasaremos a crear nuestro objeto, el cual lo representaremos con un vector; nos vamos a la tercera ventana de la barra de herramientas y seleccionamos la opción de vector pondremos su base sobre el eje x y el otro extremo por encima de este:
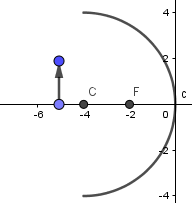
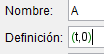
Este vector esta fijo y para recrear todos los casos que queramos necesitamos que se mueva entonces modificaremos la definición de los puntos que lo crean, para el punto de la base pondremos una definición de (t,0)
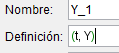
Para el punto en el otro extremo crearemos un deslizador "Y" que corresponderá con el tamaño; con esto lograremos que además de mover el objeto a lo largo del eje x podamos aumentar su tamaño, creado el deslizador pasaremos a modificar la definición del punto colocando (t,Y):
Terminado de hacer lo anterior ya nuestro objeto no estará fijo y lo podremos mover a lo largo del eje mediante el deslizador "t":
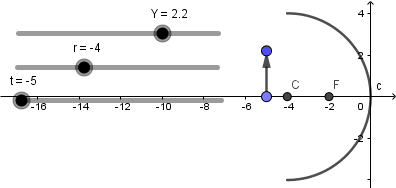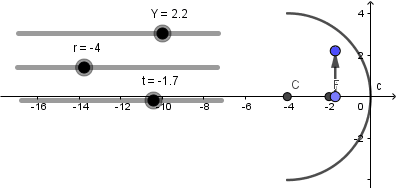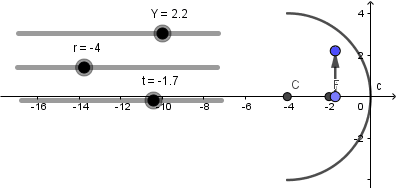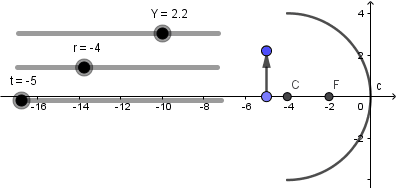
Y mediante el deslizador "Y" podemos variar el tamaño del objeto:
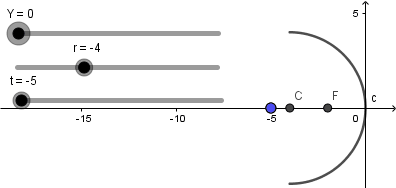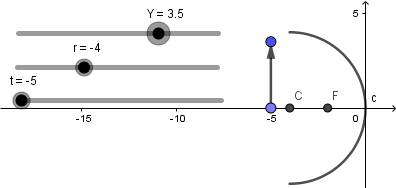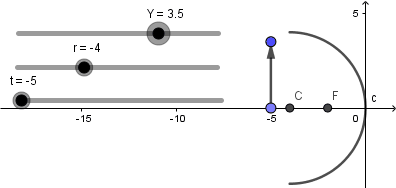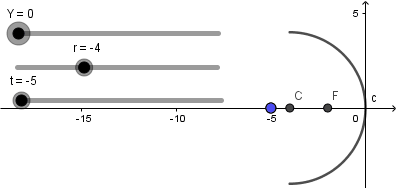
Ahora viene lo que sea quizás la parte más interesante; poner en práctica las propiedades de reversibilidad y crear los rayos que emergen del objeto y los reflejados por el espejo, empecemos creando el rayo que incide sobre el espejo paralelo al eje x.
Para crear el rayo que incide paralelo al eje nos iremos a la tercera ventana de la barra de herramientas y seleccionaremos la opción de "paralela", una vez seleccionada daremos click sobre el punto superior del objeto y luego sobre el eje x:
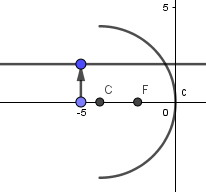
El rayo que incide paralelo al eje se refleja pasando por el foco, para ejemplificar esto primero crearemos un punto en la intersección de la recta que simula el rayo incidente con la superficie del espejo:
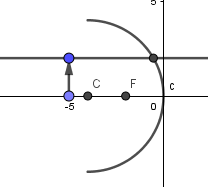
Luego de hecho esto crearemos una recta que pase por el foco y el punto de la intersección, esta será el rayo reflejado.
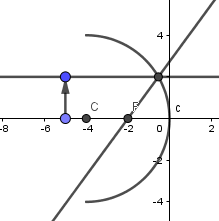
Ya tenemos nuestro primer rayo necesario para la formación de la imagen, ahora pasaremos a construir el que pasa por el centro de curvatura. Simplemente crearemos una recta que pase por el punto superior del objeto y por el centro de curvatura.
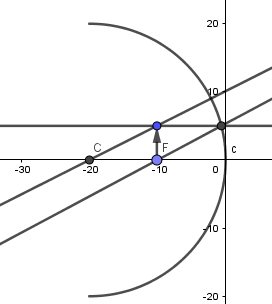
Luego de esto tenemos gran parte de nuestra simulación hecha, como dije antes en el punto donde se cortan los rayos reflejados es el lugar donde se forma la imagen por lo tanto; crearemos un nuevo vector que ejemplificará la imagen formada.
Para empezar crearemos un punto en la intersección de los dos rayos:
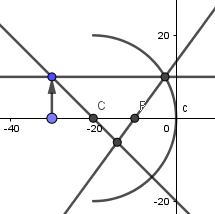
Luego de haber creado el punto pasaremos a crear una recta perpendicular al eje x sobre ese punto, nos vamos a la cuarta ventana de la barra de herramientas y seleccionamos la opción de perpendicular hacemos click sobre el punto en la intersección y luego sobre el eje x.
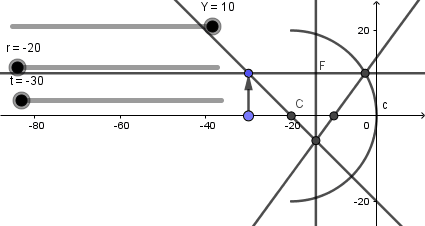
Como vemos tenemos una recta moviéndose conforme se mueve el objeto, ahora sobre esta recta crearemos nuestro vector imagen con base en el eje x y el otro extremo en la intersección de los rayos reflejados.
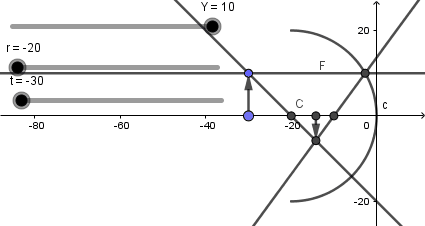
Hecho todo lo anterior podemos decir que tenemos nuestra primera simulación lista y podemos empezar a estudiar los diferentes casos, variando el radio de curvatura, el tamaño del objeto y su posición respecto al espejo. Para terminar la simulación ocultamos los objetos innecesarios, agregamos colores, estilos de línea entre otros:
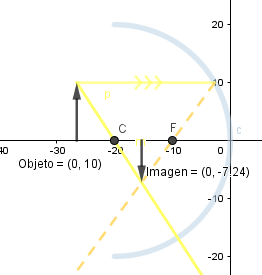

Ejemplos formación de imagen en espejo cóncavo.
Disminuyendo el radio de curvatura.
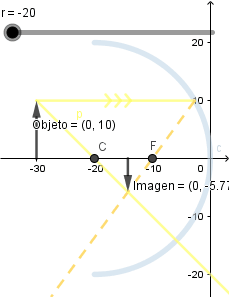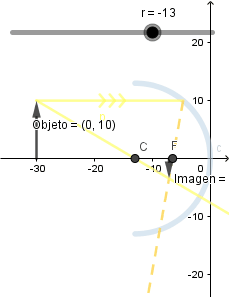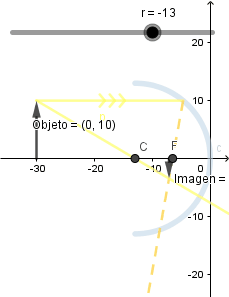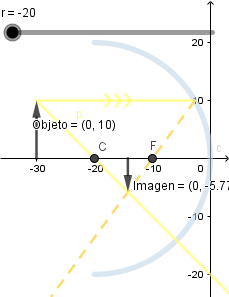
Al disminuir el radio de curvatura del espejo y mantener el objeto en la misma posición la imagen que se forma es de menor tamaño.
Objeto situado delante del foco.
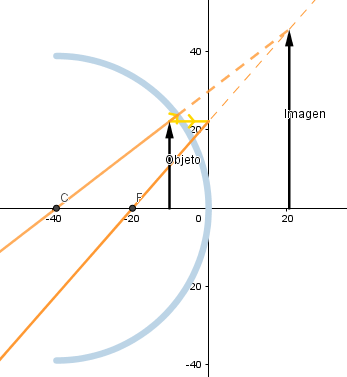
Si el objeto se encuentra situado a una distancia menor que la distancia focal la imagen se forma debido a las prolongaciones de los rayos reflejados considerándose "virtual" ademas su tamaño es mayor que el del objeto.
Objeto situado en el foco.

Los rayos son paralelos entre sí y nunca convergen, no se forma imagen.
Objeto situado entre el foco y el centro de curvatura.
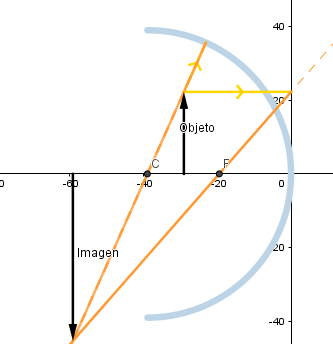
La imagen se forma por los propios rayos y no sus prolongaciones debido a esto se le llama imagen real, es de mayor tamaño que el objeto y se verá al revés.
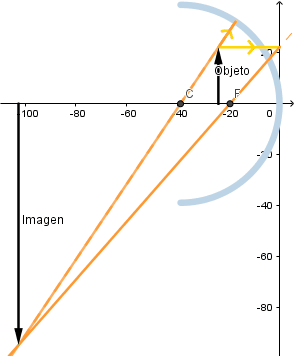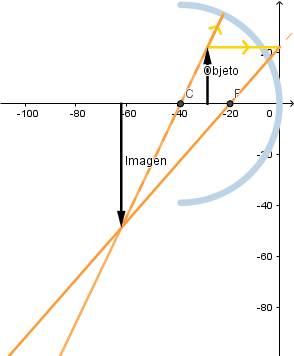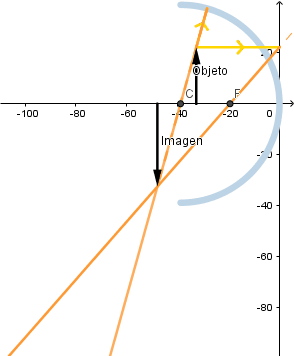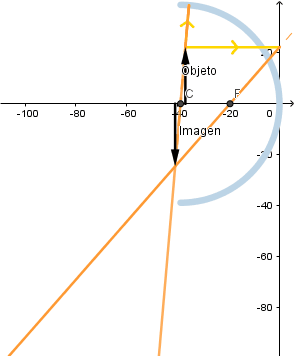
Si el objeto está entre el centro de curvatura y el foco al irse acercando al centro de curva la imagen va disminuyendo su tamaño.
Objeto en el centro de curvatura.
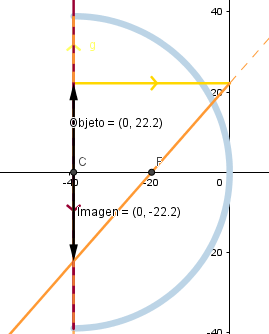
La imagen formada es real, de igual tamaño que el objeto e invertida.
Objeto más allá del centro de curvatura.
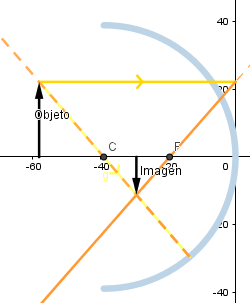
La imagen formada es invertida y de menor tamaño que el objeto.
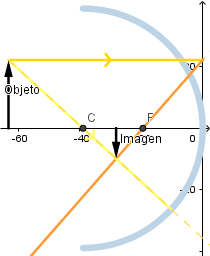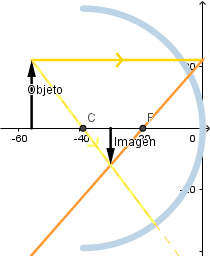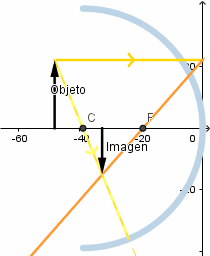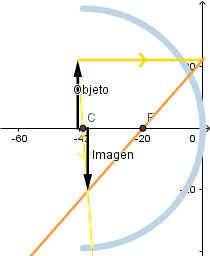
Mientras mas alejado esté el objeto del vértice del espejo el tamaño de la imagen es menor.

Construcción simulación espejo convexo.
Los pasos a seguir son prácticamente los mismos las diferencias son la posición del foco y el centro de curvatura; nuevamente empezaremos creando la forma del espejo convexo haciendo uso de la herramienta
arco de tres puntos:
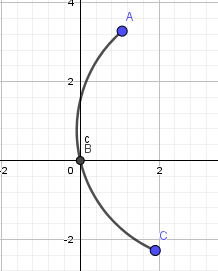
Como en la simulación anterior pasaremos a modificar el arco, entrando en su definición y cambiandola por lo siguiente:
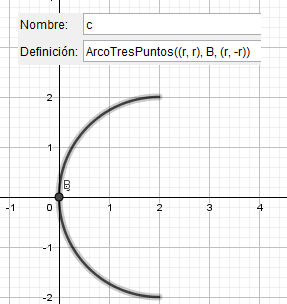
Luego pasamos a crear el centro y el foco, para el centro como en el caso anterior un punto con definicion (r,0) y el foco con definicion (r/2,0)
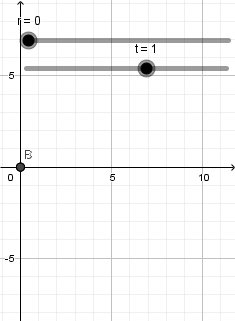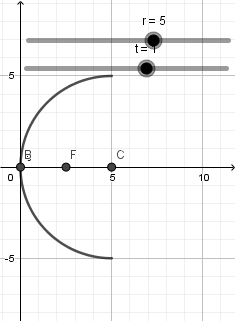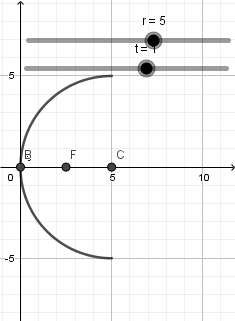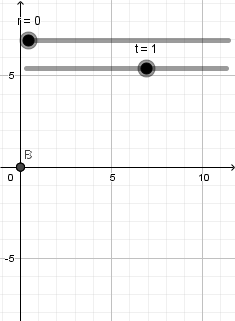
Recordemos que en un espejo convexo el radio de curvatura es mayor que cero r>0 y esto debemos especificarlo en el intervalo de nuestro deslizador simplemente ponemos en valor inicial "0" y valor final lo que deseemos.
De aquí en adelante los pasos son los mismos que en el caso anterior tanto para la creación del objeto, los rayos incidentes, reflejados y la creación de la imagen así que los obviare; luego de agregar los detalles obtenemos nuestra simulacion:
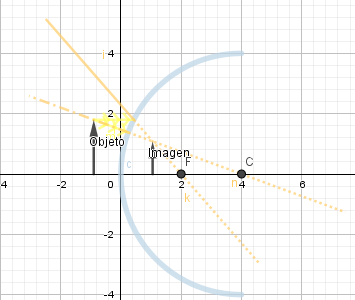
Ejemplos formación de imagen en espejo convexo.

La imagen siempre en derecha, virtual y de menor tamaño que el objeto.

Construcción simulación: formación de imágenes en lentes.
Lente biconvexa.
Debemos empezar creando nuestra lente, para esto seguiremos haciendo uso de la herramienta arco de tres puntos y haremos la forma de una lente convexa.
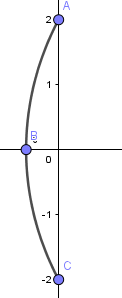
Luego creamos de la misma forma el otro lado de la lente.
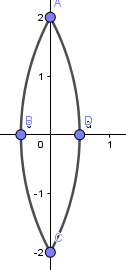
En el origen tenemos el centro óptico de la lente, así que creamos un punto ahí:
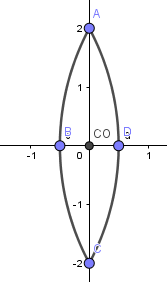
Luego crearemos una recta perpendicular al eje x en el punto del centro óptico, esta nos servirá como referencia para crear los rayos.
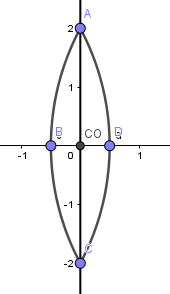
Luego de creada nuestra lente podemos establecer los focos respectivos simplemente colocamos los puntos donde corresponde:
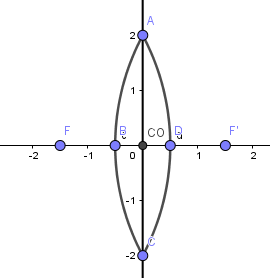
Luego de todo esto crearemos nuestro objeto de la misma forma que en los casos anteriores:
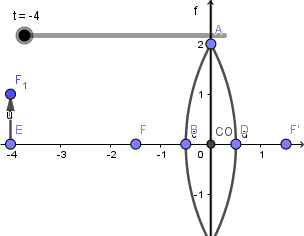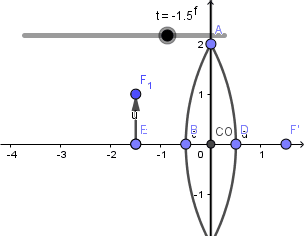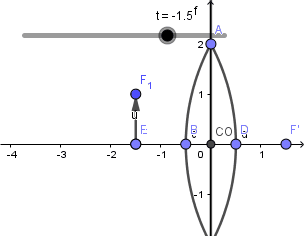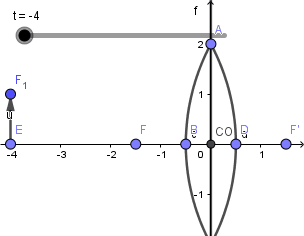
Listo el objeto podemos empezar a crear los rayos incidentes y refractados, en una lente tenemos la diferencia que hay dos focos; el foco objeto y el foco imagen así que debemos aplicar las propiedades de reversibilidad para ambos, además en vez del centro de curvatura tenemos el centro óptico por donde debemos trazar un rayo.
Empecemos creando el rayo que pasa por el foco objeto, hacemos uso de la herramienta recta y la creamos haciendo que pase por el punto superior del objeto y el foco objeto:
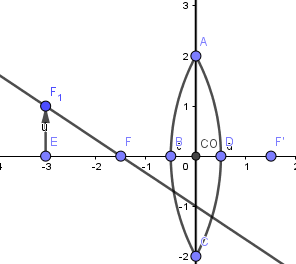
En la intercepcion del rayo incidente y la recta perpendicular al centro óptico crearemos un punto, el cual servirá como referencia para crear el rayo que emerge lo cual lo hace desde ahí:
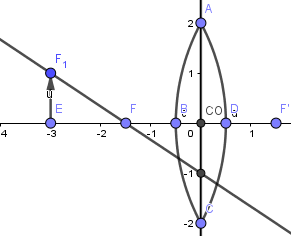
Debido a la propiedad de reversibilidad el rayo refractado emerge paralelo al eje, así que lo crearemos usando la herramienta de paralela seleccionando el punto antes creado:
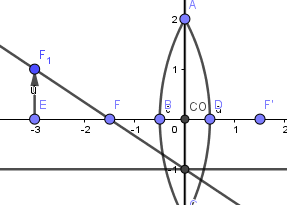
Ya tenemos nuestros primeros rayos, ahora crearemos un rayo que incide paralelo al eje; al emerger pasa por el foco imagen:

De igual forma en la interceptor del rayo y la recta perpendicular al centro óptico crearemos un punto y a partir de el, el rayo refractado que pasa por el foco imagen:
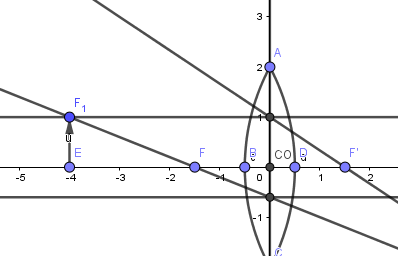
Creados los dos rayos anteriores solo nos falta crear el rayo que incide pasando por el centro óptico de la lente, este emerge sin desviarse, así que basta crear una recta que pase por el punto superior del objeto y el centro óptico:
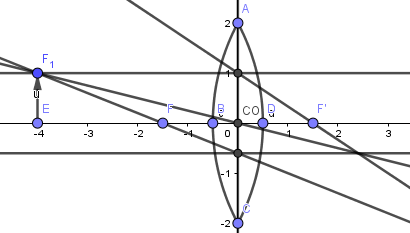
Como vemos todos los rayos refractados se cortan en un punto, es ahí donde se forma la imagen así que pasaremos a crear el vector correspondiente como hemos hecho en los casos anteriores:
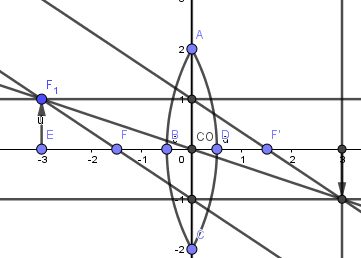
Luego de haber seguido todos los pasos anteriores podemos decir que ya tenemos la simulación lista, solo hay que convertir esa fea estructura gris en algo mas visto; pasamos a ocultar los objetos innecesarios, agregar colores y estilo de lineas:
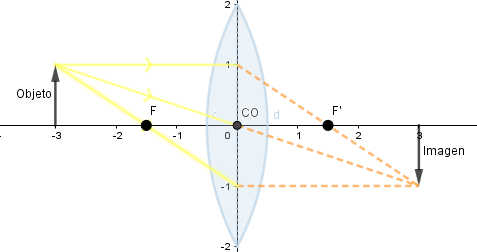
Ejemplos formación de imagen en lente biconvexa (Convergente).
Objeto situado más allá de la distancia focal.
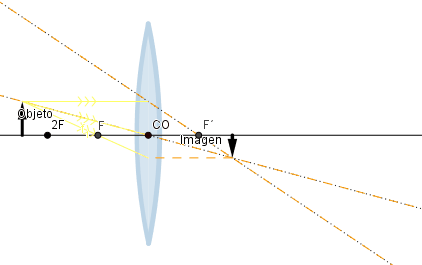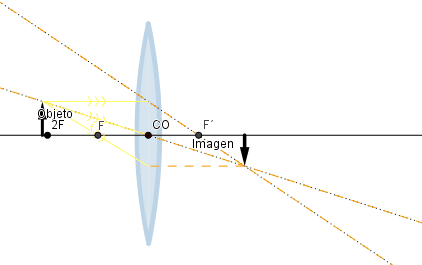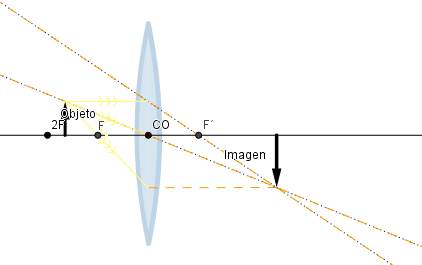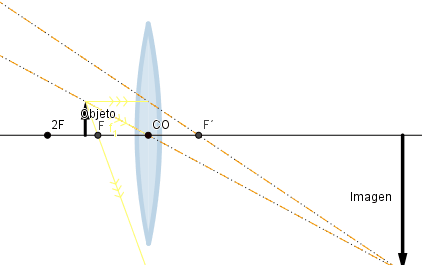
Si el objeto se sitúa a una distancia mayor que dos veces la distancia focal la imagen formada es de menor tamaño, pero si se encuentra a una distancia mayor que la distancia focal pero menor que dos veces esta el tamaño de la imagen formada es más grande que la del objeto, en ambos casos la imagen se verá al revés.
Objeto situado en el foco.
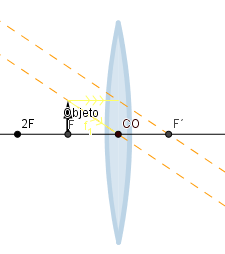
En este caso no se forma imagen los rayos nunca convergen en un punto.
Objeto situado a una distancia menor que la distancia focal.
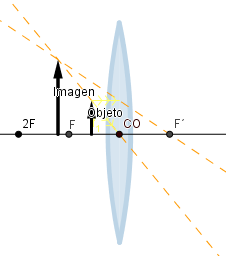
La imagen que se forma es de mayor tamaño que el objeto, real y no invertida.
Lente bicóncava.
Para este tipo de lente la construcción de los rayos cambia debido a que todo rayo que incida en la lente paralelo al eje es la prolongación del rayo que emerge la que pasa por el foco objeto y de igual forma todo rayo que incida pasando por el centro óptico emerge sin desviarse. Sin embargo, obviando esto y la forma de la lente la cual se crea de igual forma con la herramienta Arco de tres puntas los pasos a seguir son exactamente los mismos.
Ejemplos formación de imagen en lente bicónvaca (divergente).
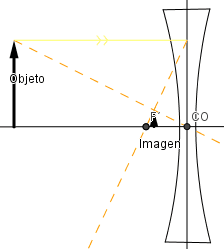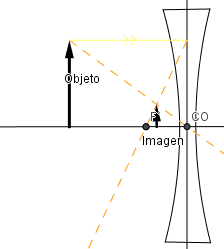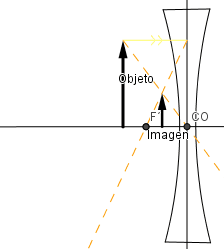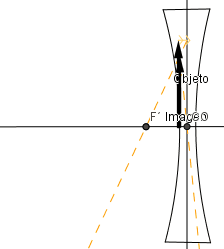
Sin importar la ubicación del objeto siempre la imagen es virtual, no invertida y de menor tamaño que el objeto.
Y así terminamos con las simulaciones sobre tan interesante fenómeno que vivimos a diario como es la formación de las imágenes en lentes y espejos.
En mi aprendizaje sobre el funcionamiento de este software me dispuse a crear una pequeña simulación sobre el funcionamiento del ojo humano debido que este es un sistema óptico; si bien es muy complejo se puede hacer un pequeño estudio de el debido a que el cristalino es una lente convergente, diferenciándose de las que hemos visto en que tiene la capacidad de variar su curvatura dependiendo del enfoque necesario para que la imagen se logre formar sobre la retina; debido a que para lograr ver con claridad la imagen debe formarse sobre esta.
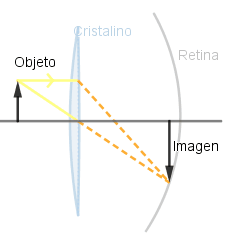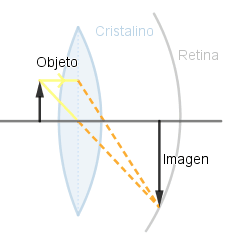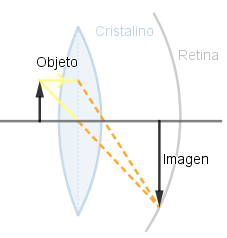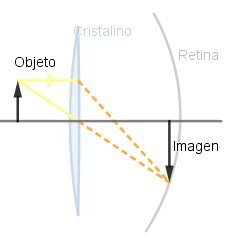
Al poder variar su curvatura el foco se encuentra a diferentes distancias logrando con esto que la imagen se forme en la retina.
Si el cristalino fuese rígido.
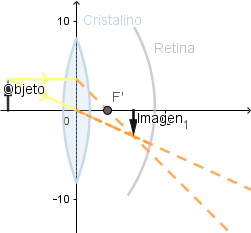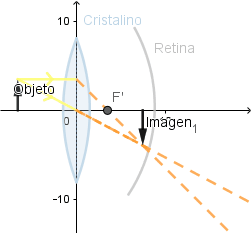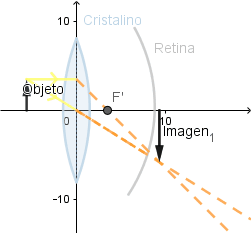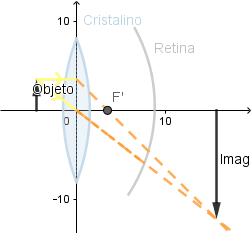
La imagen no logra formarse en todo momento sobre la retina.
Espero hayan disfrutado de este post y aprendido como se forman las imágenes y un poco mas sobre la utilización del software.

( Todas las imágenes y animaciones han sido hechos por mi usando el software matemático GeoGebra Classic 5.)
Material consultado:
Resnick, Halliday, Krane, (1992). Física Vol. 2. 4ta edición compañía Editorial Continental México.
Font, J. (2003). Óptica geométrica. Universidad Politécnica de Cataluña. http://aransa.upc.es/ffettsi/Apuntes/Optica.pdf
Para leer contenido de calidad sobre ciencia los invito a visitar la etiqueta #stem-espanol
Si estas interesado en publicar contenido sobre Física, te invito cordialmente a unirte al sub-grupo #fisica del chat de stem-espanol en discord.

Imagen creada por @djredimi2


























































Estas participando para optar a la mención especial, que se efectuará el 29 de Julio del 2018 a las 8:00 pm (hora de Venezuela); donde el autor del artículo seleccionado recibirá la cantidad de 1 SBD transferidos a su cuenta.
Contáctanos en Discord: https://discord.gg/hkCjFeb
Apoya al trail de entropía y así podrás ganar recompensas de curación de forma automática, entra aquí para más información sobre nuestro TRAIL.
Puedes consultar el reporte diario de curación visitando @entropia
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Saludos @luiscd8a. Excelente trabajo. Muy bien explicado. Las aplicaciones que nos muestras son de primera.
Gracias por su apoyo profesor @lorenzor, seguiré mejorando para obtener mayores resultados.
Saludos @luiscd8a se noto el arduo trabajo en la diagramación del artículo te felicito hermano, me gustaría alguna orientación de como crear una imagen gif! nos seguimos leyendo !
Muchas gracias por tu comentario @amestyj, puedes leer este artículo es una pequeña introducción que hice al software GeoGebra ahí puedes ver cómo crear las animaciones, luego de ese vienen un par más donde voy explicando con ejemplos el uso de las herramientas.
Saludos.
Gracias hermano por tu apoyo y sugerencias .!
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!