En mis post anteriores les hable sobre tres curvas del tipo ruleta cicloidal, curvas que considero fantásticas por sus propiedades, características y formas; si no tuvieron la oportunidad de leerlos acá les concentro las características y propiedades más interesantes de estas curvas: Cicloide, Epicicloide e Hipocicloide.
La Cicloide.
La Cicloide, la madre de la epicicloide y la hipocicloide es la curva que describe un punto sobre una circunferencia que rueda sin deslizar sobre una recta, estudiada ampliamente en el siglo XVII creó disputas entre los científicos de la época ganándose el apodo de "la Helena de los geómetras" siendo Galileo Galilei el primero en hacer un estudio riguroso de ella y quien acuñó el término.
Cicloide normal:
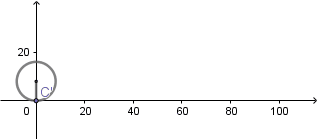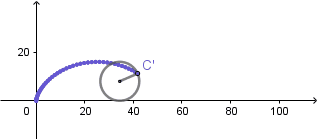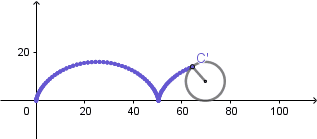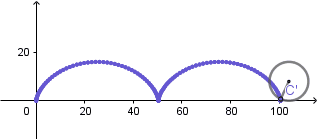 (GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
La Cicloide tiene dos interesantes propiedades:
- Tautócrana: Huygens en su intento de crear un reloj que funcionara de manera perfecta haciendo uso del péndulo cicloidal descubrió que una partícula alcanza el fondo de un arco cicloidal invertido en la misma cantidad de tiempo sin importar desde que punto del arco comience su descenso. Asi una curva tautócrana es en la cual partiendo desde cualquier punto A sobre ella se llega en la misma cantidad de tiempo al punto B.
Ejemplo tautócrana:
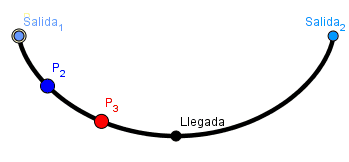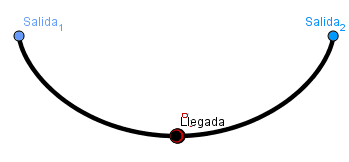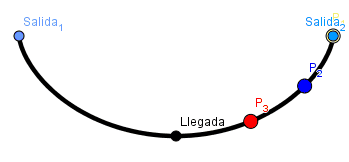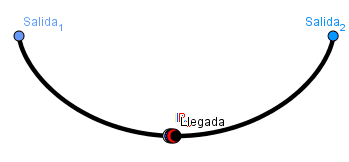 (GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
- Braquistócrona: significa "el menor tiempo" y es la trayectoria por la cual se debe mover un objeto para ir en el menor tiempo posible de un punto A hasta un punto B, quizás pensemos que es una línea recta pero no, de hecho es uno de los caminos más lentos. Este problema fue resuelto por Bernoulli haciendo uso del cálculo variacional en el cual obtuvo como resultado una Cicloide, siendo esta entonces la braquistócrona.
Ejemplo braquistócrona:
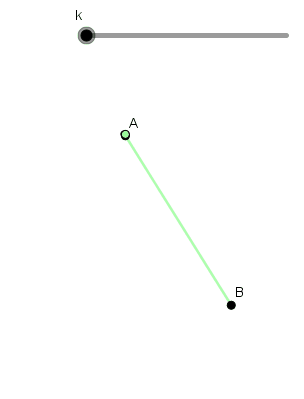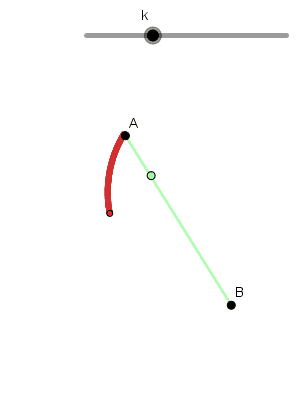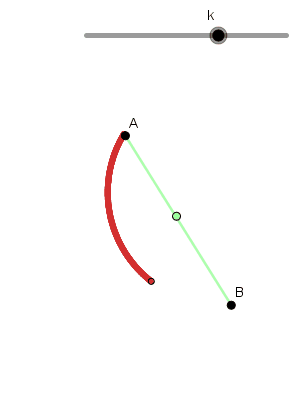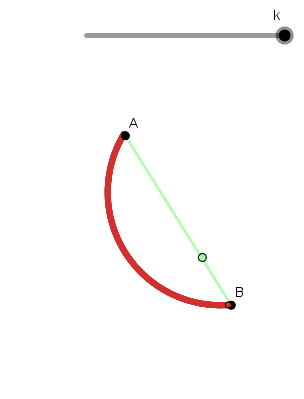
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
Como podemos ver el punto que llega primero a "B" es el que su trayectoria describe un arco cicloidal.
¿Y qué tal si ahora dejamos lo simplista y en vez de hacer rodar la circunferencia sobre una recta la hacemos rodar en la parte exterior de otra circunferencia? Cuando esto ocurre obtenemos una
epicicloide
que es la curva que describe la trayectoria de un punto sobre una circunferencia generatriz que rueda sobre una circunferencia directriz sin deslizamiento.
Ejemplo epicicloide:
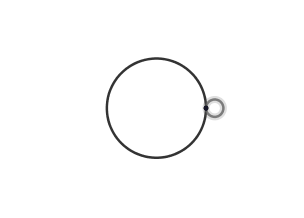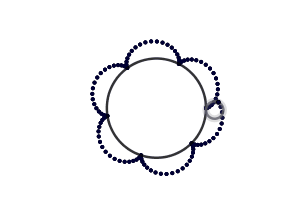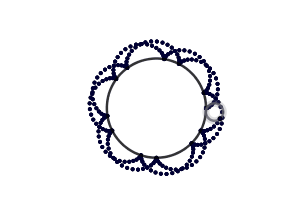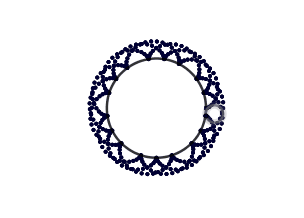
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
Ecuaciones paramétricas de la epicicloide:
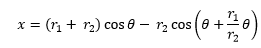 ;
; 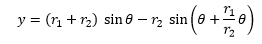
Una de las primeras cosas interesantes de la epicicloide son las figuras que se pueden obtener al variar el radio de las circunferencias, estás figuras están determinadas por el cociente del radio de la circunferencia directriz y la generatriz el cual llamaremos "k", cuando "k" es un número entero nuestra epicicloide tendrá igual número de cuspides que "k".
k = 1. Cardioide.
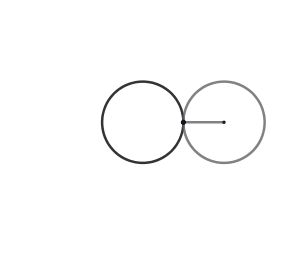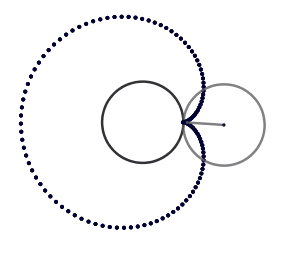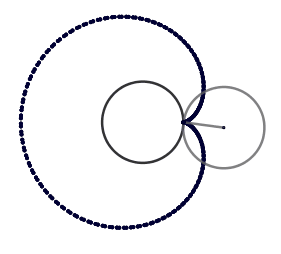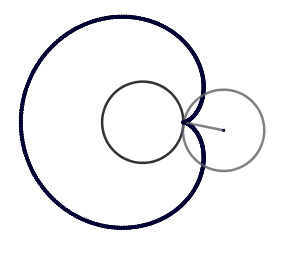 (GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
El cardioide es el caso más sencillo de una epicicloide y quizás el más conocido su nombre proviene de la similitud con un corazón, lo más interesante del cardioide es que aparece de forma natural como la envolvente de los rayos de luz reflejados por una circunferencia cuando el foco está en el borde de esta, esto se conoce como cáustica . Las cáusticas aparecen de diversas maneras el ejemplo más sencillo es cuando tenemos un vaso de cristal con agua iluminado por los rayos de sol, al proyectarse la sombra podemos ver zonas brillantes las cuáles son las cáusticas.
Simulación del fenómeno.
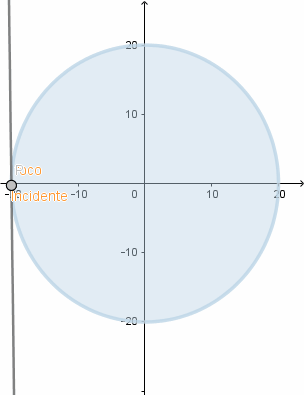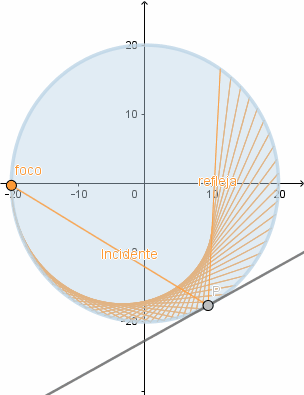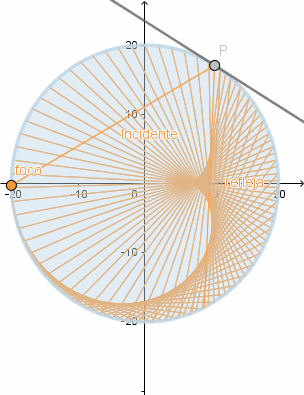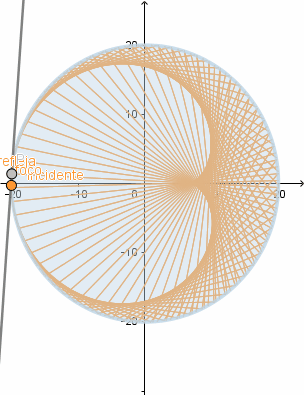 (GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
Lo anteriormente dicho hecho realidad.
 (Foto tomada por mi con mi celular Siragon SP-5050)
k = 2. Nefroide.
(Foto tomada por mi con mi celular Siragon SP-5050)
k = 2. Nefroide.
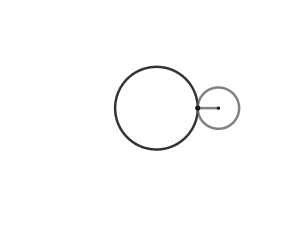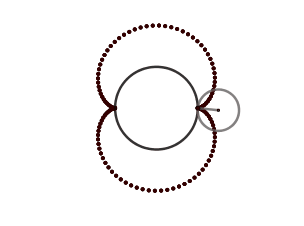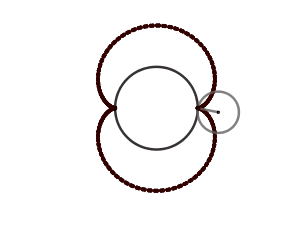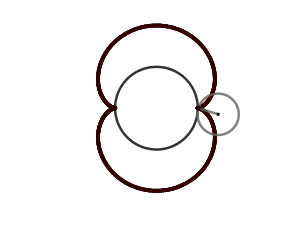
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
El nefroide es otra interesante epicicloide que de igual forma aparece como la envolvente de los rayos de luz reflejados por una circunferencia, siendo la diferencia que para que esto ocurra el foco debe estar fuera de la circunferencia.
Simulación de lo anteriormente dicho.
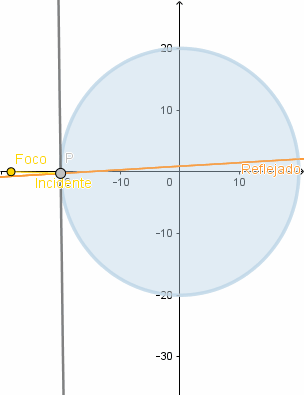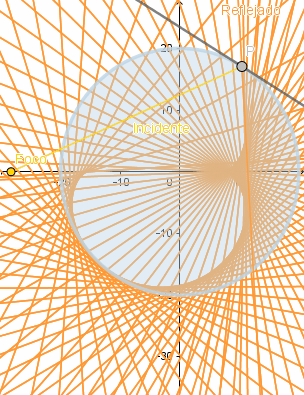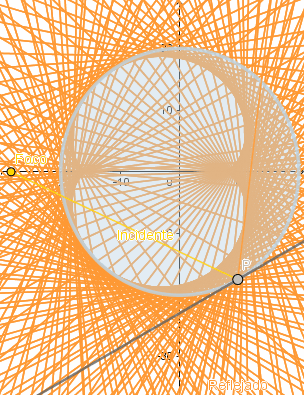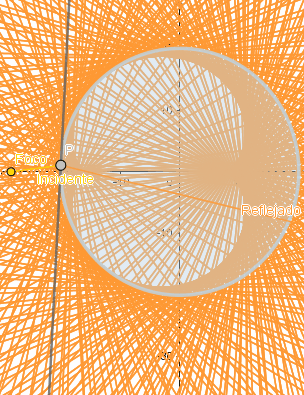
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
k = 10/3
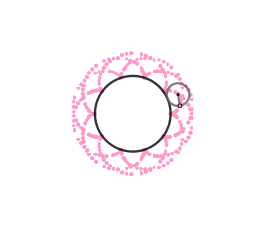 (Imagen creada por mi usando el software matemático GeoGebra Classic 5)
(Imagen creada por mi usando el software matemático GeoGebra Classic 5)
¿Y por qué no hacemos rodar la circunferencia generatriz dentro de la circunferencia directriz?
Cuando hacemos esto obtenemos una
hipocicloide
que es la curva que describe la trayectoria de un punto sin deslizar sobre una circunferencia que rueda por el interior de una circunferencia directriz sin deslizamiento.
Ejemplo hipocicloide:
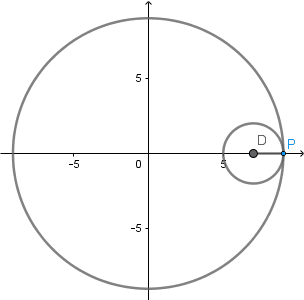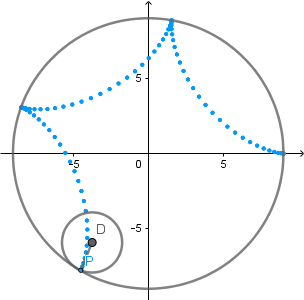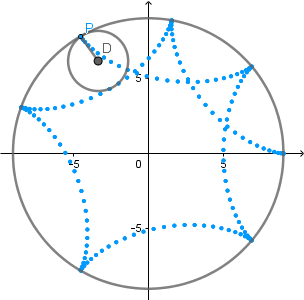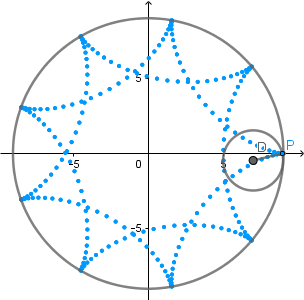 (GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
Ecuaciones paramétricas hipocicloide.
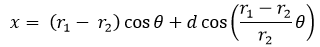 ;
; 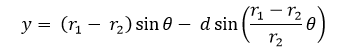
De igual forma las figuras generadas vienen determinadas por el cociente "k".
k = 3. Deltoide.
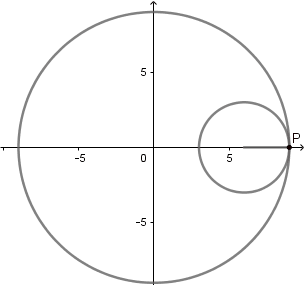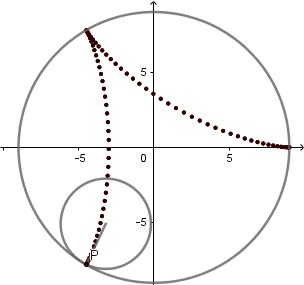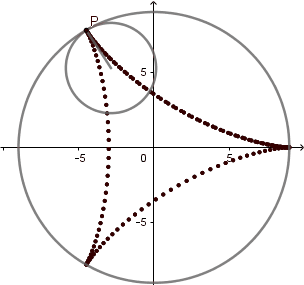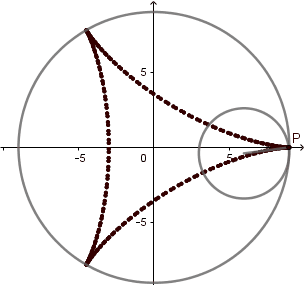 (GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
k = 4. Astroide.
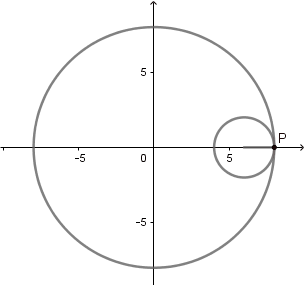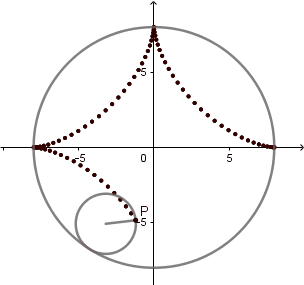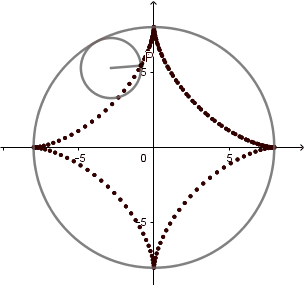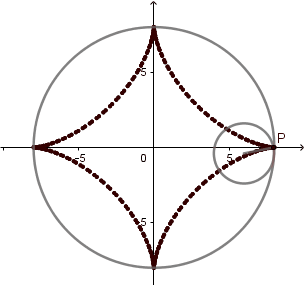
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
k = 9/4
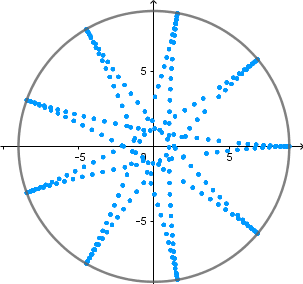
(Imagen creada por mi usando el software matemático GeoGebra Classic 5)

Algo en común que tienen estas tres curvas a demás de ser generadas por la trayectoria de un punto sobre una circunferencia es que, podemos tener dos casos más de ellas; cuando el punto que describe la curva está fuera de la circunferencia generatriz llamándose cicloide, epicicloide o hipocicloide "alargada" dependiendo del tipo y cuando el punto se encuentra en el interior de la circunferencia generatriz llamándose "acortada".
Ejemplos:
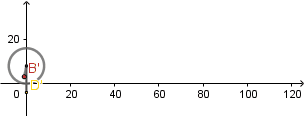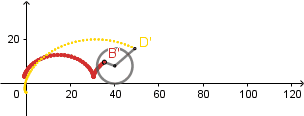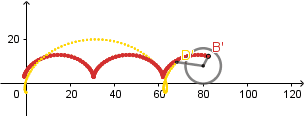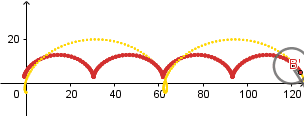 (GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
Como podemos ver el punto rojo está dentro de la circunferencia describiendo una cicloide acortada, a su vez el punto amarillo está fuera de la circunferencia generando una cicloide alargada.
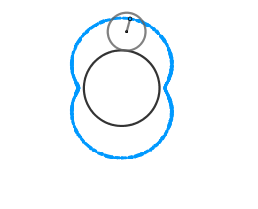
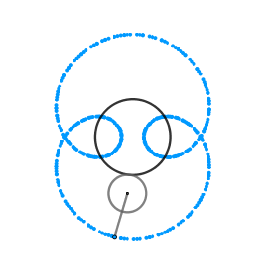
En las imagenes de arriba podemos ver una epicicloide acortada y alargada respectivamente ambas con k = 2 que seria una nefroide.
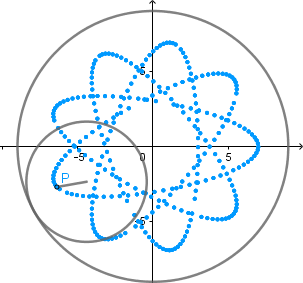
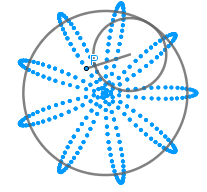
Podemos ver dos hipocicloides una acortada y otra alargada respectivamente, ambas con k=9/4 como en el ultimo ejemplo de hipocicloide normal.
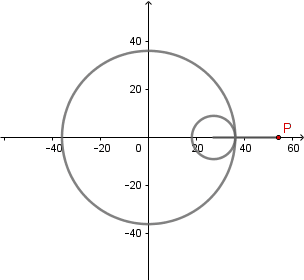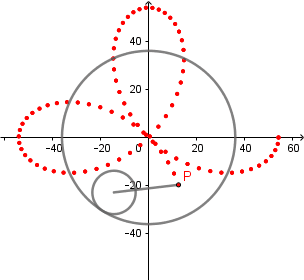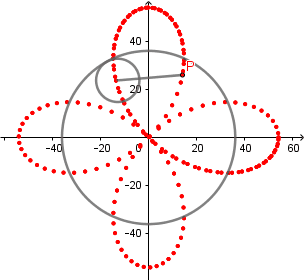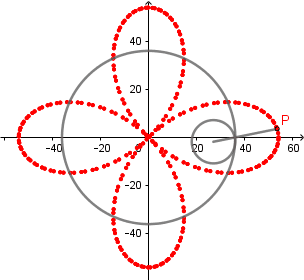
La hipocicloide presenta casos bastante interesantes en comparación con las otras dos curvas bajo estas modalidades, una de estas es que podemos obtener la familia de curvas llamada "rosa polar" como un caso especial de una hipocicloide alargada cuando 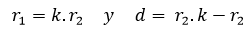 . El numero de "pétalos" de nuestra rosa vendrá dado por "k".
. El numero de "pétalos" de nuestra rosa vendrá dado por "k".
k = 3. Trifolium.
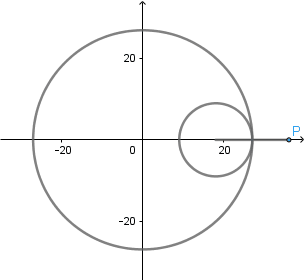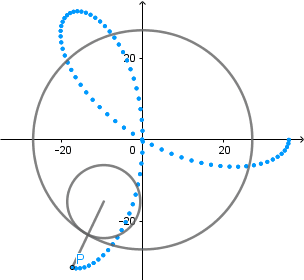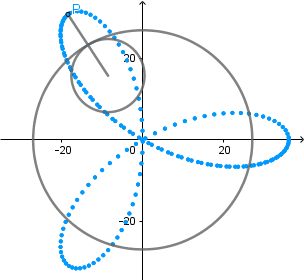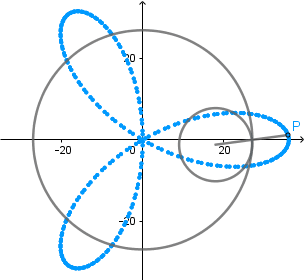
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
k = 4. Cuatrifolium.
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
k = 8.
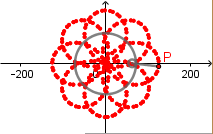
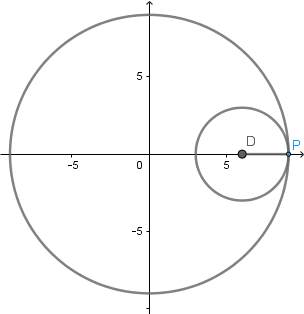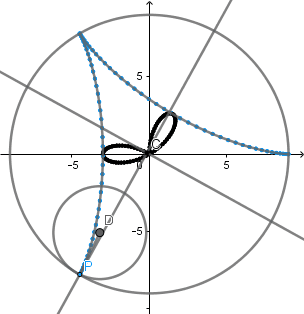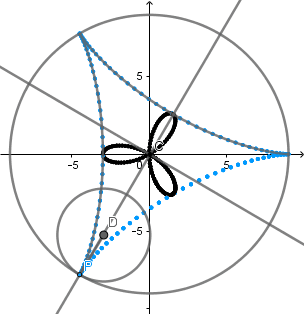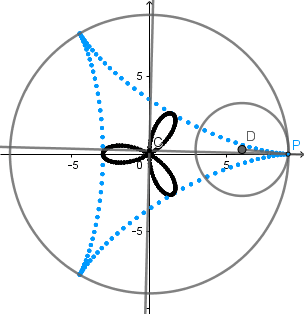
Aparte de esta relación entre la hipocicloide alargada y la rosa polar podemos encontrar una muy interesante relación entre la hipocicloide ordinaria y la rosa polar y es que, el lugar geometrico formado por los puntos de corte entre cada tangente a la hipocicloide y la perpendicular a la tangente respecto a un punto en el centro de la circunferencia directriz es una rosa polar.
Ejemplos:
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
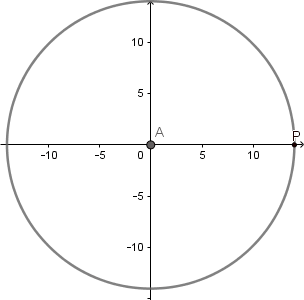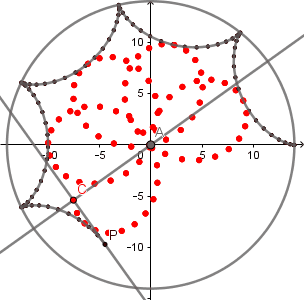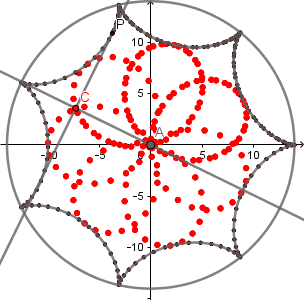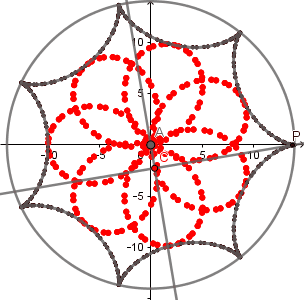
(GIF creado por mi usando el software matemático GeoGebra Classic 5)
Como podemos ver al aumentar el numero de vértices de nuestra hipocicloide aumenta de igual forma el numero de "pétalos" de nuestra rosa polar, la figura que se está formando en el centro es la
podaria
de la curva hipocicloide.

Espero hayan disfrutado de estas fascinantes curvas y sus propiedades, si estan interesados en información mas detallada sobre ellas pueden revisar en mi blog los artículos individuales de cada una.
Todas las imágenes y GIF's han sido hechos por mi usando el software matemático GeoGebra Classic 5.
Material consultado:
T. Soldovieri, (2017), Introducción a la mecánica clásica, Venezuela, 1era edición, P.P. 455-457.
De Gante, C. Generación y Comparación de Patrones de
Difracción de Aberturas Poligonales e
Hipocicloides. Benemérita Universidad Autónoma De Puebla Facultad De Ciencias Físico Matemáticas.
https://www.fcfm.buap.mx/assets/docs/docencia/tesis/fisica/2014/DeGanteGonzalezCesar.pdf
Corcho, F. (2017). La cicloide. Universidad de Sevilla Departamento de Geometría y Topología.
https://idus.us.es/xmlui/bitstream/handle/11441/63117/Corcho%20Guti%C3%A9rrez%20Fernando%20Manuel%20TFG.pdf?sequence=1
Rodriguez, R., Concepción, C. M. (2011). CURVAS MARAVILLOSAS. Facultad de matemática física y computación.
http://dspace.uclv.edu.cu/bitstream/handle/123456789/9206/Trabajo%20de%20diploma%20%28Raydel%20y%20Cindy%29.pdf?sequence=1&isAllowed=y




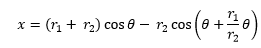 ;
; 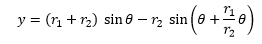







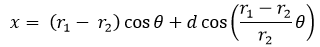 ;
; 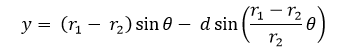









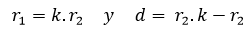 . El numero de "pétalos" de nuestra rosa vendrá dado por "k".
. El numero de "pétalos" de nuestra rosa vendrá dado por "k".






Buen post, veo que le has dedicado tiempo al Geogebra, particularmente no he tenido oportunidad de trabajarlo aunque se ve muy interesante, saludos.
Muchas gracias @ydavgonzalez agradecido de tenerte por acá, GeoGebra es estupendo te lo recomiendo ampliamente.
Hola @luiscd8a Excelente manera de explicar un tema tan complejo. Gracias por el aporte.
Gracias por el apoyo!