Demostración experimental de la ley de Biot - Savart
¡Hola amigos de Steemit!
Reciban un cordial saludo.
En la actualidad, las tecnologías más avanzadas han sido posibles gracias a los grandes descubrimientos que hemos logrado en un área de vital interés conocida hoy en día con el nombre de Electromagnetismo.
Por un breve tiempo se pensó que la electricidad y el magnetismo eran fenómenos físicos independientes, hasta que las observaciones realizadas por Hans Christian Oersted mostraron una conexión entre el flujo de cargas eléctricas (corriente eléctrica) y la deflexión que experimenta la aguja imantada de una brújula, convirtiendo esta observación en la primera evidencia experimental del origen de un campo magnético debido al movimiento de cargas eléctricas en un conductor.
Sin embargo, estas observaciones realizadas por el gran Oersted carecieron de una formulación matemática, hasta el momento en el que los renombrados científicos Jean-Baptiste Biot y Félix Savart obtuvieron una ecuación, la cual permitía determinar la magnitud y dirección del campo magnético que un conductor establece en su entorno cuando por este circula una corriente eléctrica.
Sin lugar a dudas, la determinación del campo magnético a partir de la ley de Biot-Savart representa uno de los logros más importante del electromagnetismo clásico y, desde entonces, ha sido una herramienta valiosa en la obtención del campo magnético generado por distintas distribuciones de corriente.
Gran parte de las más avanzadas tecnologías están compuestas por elementos generadores de campo magnético, cuyos principios están soportados en la ley de Biot-Savart.
Dada su importancia en este artículo presentaré un pequeño análisis teórico y experimental de la ley de Biot-Savart, con el fin de fortalecer nuestros conocimientos en una de las leyes cuyo impacto ha permitido importantes avances científicos y tecnológicos.
Fundamentos teóricos
Las observaciones experimentales realizadas por Biot y Savart permitieron concluir que, el campo magnético originado por una corriente en un conductor presenta una proporcionalidad inversa con la distancia al punto donde dicho campo es determinado, mientras que presenta una proporcionalidad directa con la corriente eléctrica responsable de generar este campo, tal y como se observa en la siguiente expresión:
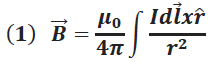
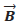→ Densidad de flujo magnético ( Tesla).
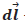→ Diferencial de longitud en la dirección de I (m).
r → Distancia desde el elemento diferencial hasta P (m).
→ Vector unitario en la dirección del vector 
.
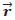μ0 →Constante de permeabilidad magnética en el vacío
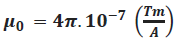
I → Intensidad de la corriente eléctrica en el conductor.
Los resultados experimentales indicaban, además, que la dirección del campo magnético resultante es perpendicular al plano donde subyacen los vectores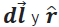 
.
.
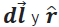En la siguiente imagen se ilustra la relación geométrica entre los parámetros de campo magnético y corriente en un conductor, obtenida por Biot y Savart como resultado de sus observaciones experimentales.
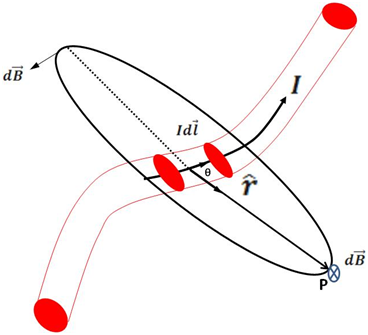
(Elaborado por @lorenzor en PowerPoint)
En la siguiente sección obtendremos, a partir de la ley de Biot–Savart, el campo magnético generado por algunas de las distribuciones de corriente más comunes.
Campo magnético generado por un conductor Rectilíneo en un punto P
Un conductor rectilíneo es uno de los casos más simples de distribuciones de corriente generadores de campo magnético. De acuerdo a las dimensiones del conductor, estos campos pueden clasificarse en: campos debido a conductores largos o campos debido a conductores cortos.
Para un conductor corto (finito) de longitud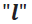 
(Ver Figura 2), el campo magnético derivado de la ley de Biot-Savart está dado por la expresión:
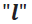(Ver Figura 2), el campo magnético derivado de la ley de Biot-Savart está dado por la expresión: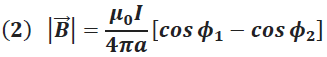
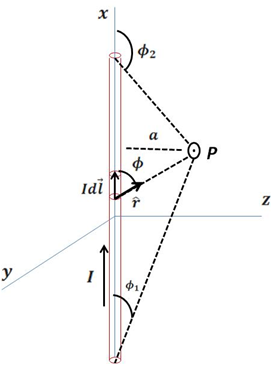
Figura 2 – Diagrama esquemático del campo magnético generado por un conductor finito
(Elaborado por @lorenzor en PowerPoint)
Para un conductor rectilíneo infinito(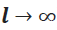
) , se tiene que 
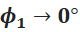y 
.
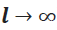) , se tiene que 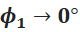y .
Esta tendencia en los ángulos simplifica la expresión (2) a una forma más simple dada por la siguiente ecuación:
Campo magnético generado por una espira
En una gran variedad de aplicaciones prácticas, los conductores en forma circular aportan beneficios debido a la uniformidad e intensidad del campo magnético generado por dichos conductores. Esta uniformidad e intensidad es aún mayor en un solenoide (bobina), el cual consiste en un arreglo de espiras muy cercanas entre sí.
A continuación se analiza el campo magnético de una espira circular, cuyo resultado es utilizado para la obtención del campo magnético de un conjunto de espiras o solenoide.
En la espira circular ilustrada en la figura 3, fluye una corriente constante "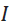
" , la cual genera un campo magnético a lo largo del eje 
.
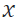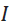" , la cual genera un campo magnético a lo largo del eje .
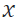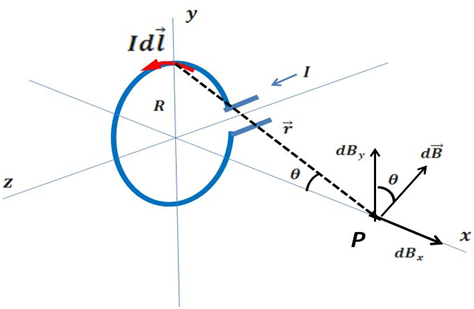
(Elaborado por @lorenzor en PowerPoint)
De la ley de Biot–Savart se obtiene, luego de un simple proceso de integración, que el campo magnético en cualquier punto del eje x es dado por la expresión:
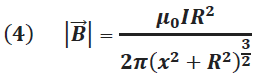
Campo magnético de un solenoide
El campo magnético de un solenoide de longitud “l" y "N" espiras es obtenido a partir de la superposición del campo magnético de cada una de las espiras constituyentes (Ver Figura 4).
Este campo resultante a lo largo del eje del solenoide es obtenido integrando la ecuación (4), el cual resulta en la siguiente expresión:
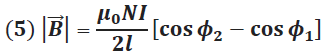
Donde:
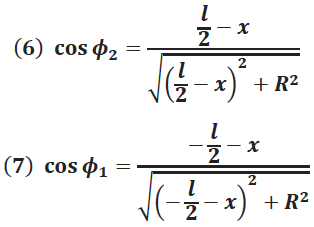
Para un solenoide donde su longitud "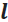
" es mucho más grande que su radio, la magnitud del campo magnético en su centro y en los extremos se simplifica a las siguientes expresiones:
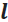" es mucho más grande que su radio, la magnitud del campo magnético en su centro y en los extremos se simplifica a las siguientes expresiones: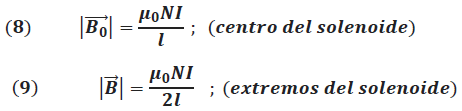
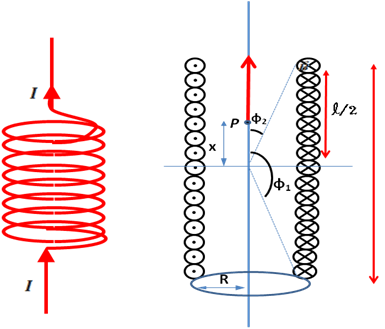
(Elaborado por @lorenzor en PowerPoint)
Campo magnético de las bobinas de Helmholtz
Las bobinas de Helmholtz, ilustradas en la figura 5, han jugado un rol importante en el campo de la investigación.
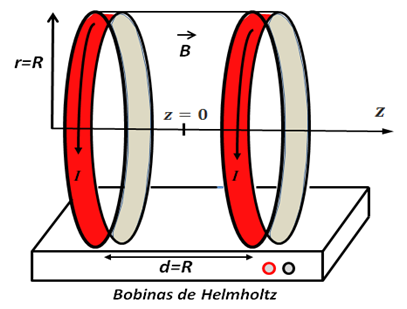
(Elaborado por @lorenzor en PowerPoint)
Entre sus aplicaciones encontramos la determinación de la relación carga-masa de un electrón, la demostración experimental de la deflexión de un haz de electrones debido a la presencia de un campo magnético y la determinación del campo magnético terrestre, el cual fue un tema desarrollado en uno de mis artículos.
Su versatilidad se debe a la uniformidad e intensidad del campo magnético existente en el área que separa las bobinas que forman este arreglo.
En general el campo magnético total en un punto del eje z, ubicado entre las dos bobinas, es obtenido a partir de la ley de Biot-Savart y está dado por la siguiente expresión:
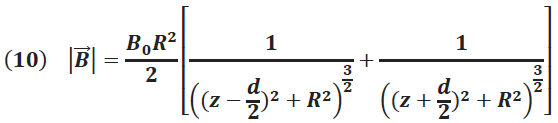
Donde:
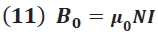
En un arreglo de Helmholtz, el radio de las bobinas es de igual magnitud que la separación entre ellas (d=R) y el campo magnético es constante en la región ubicada entre ellas, con un valor máximo en torno a su centro dado por la siguiente ecuación:
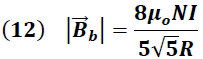
Parte experimental
Materiales y equipos utilizados
(Fotografía tomada por @lorenzor en el laboratorio y editada en PowerPoint)
Metodología
Para demostrar experimentalmente la validez de la ley de Biot-Savart utilizaremos un arreglo de Bobinas de Helmholtz y un Solenoide, en el que mediremos las distribuciones experimentales de la densidad de flujo magnético a lo largo del eje que pasa por el centro de cada una de estas configuraciones, las cuales serán comparadas con los valores teóricos de campo magnético arrojados por la ley de Biot –Savart.
Estas medidas son obtenidas utilizando un medidor digital de campo magnético de alta precisión, conocido como Teslámetro (modelo 5070), el cual está provisto de una sonda de Hall, capaz de registrar la distribución de la densidad de flujo magnético originado en las bobinas, una vez que por estas fluye una corriente eléctrica.
En la siguiente imagen se observa el montaje experimental para la obtención del campo magnético a lo largo del eje de las bobinas de Helmholtz.
(Fotografía tomada por @lorenzor en el laboratorio)
Una vez suministrada una corriente eléctrica continua (I = 1.5 A) a las bobinas, la sonda de Hall es desplazada a lo largo del eje que pasa por su centro, registrando de esta forma los valores de campo magnético en el Teslámetro (ver figura 8).
(Fotografía tomada por @lorenzor en el laboratorio)
Datos y resultados experimentales (Arreglo de Helmholtz)
N = 130 (Número de vueltas)
R = 15 cm (Radio de las bobinas)
I = 1.5 A (Corriente en las bobinas)
-7.5 cm ≤ z ≤ 7.5 cm (Separación entre las bobinas)
En la siguiente representación gráfica elaborada en la aplicación Excel, se observan los valores teóricos de campo magnético obtenidos a partir de la ecuación (10) y los valores experimentales de campo magnético dados por el Teslámetro.
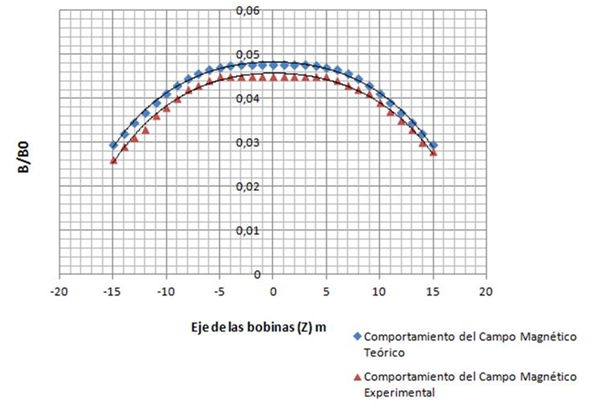
en el eje de las bobinas de Helmholtz
(Elaborado por @lorenzor en Microsoft Excel)
De forma similar, el campo magnético es medido a lo largo del eje del solenoide a intervalos de 2 cm, previamente fijados en la mesa de pruebas, tal y como se muestra en la siguiente imagen.
(Fotografía tomada por @lorenzor en el laboratorio)
Datos y resultados experimentales (Solenoide)
N = 2920
l = 11 cm
I = 0.2 A
R = 2 cm
-5.5 cm ≤ x ≤ 5.5 cm (eje de medición)
En la siguiente representación gráfica se muestran los valores teóricos de campo magnético obtenidos a partir de la ecuación (5) y los valores experimentales de campo magnético obtenidos a través del Teslámetro.
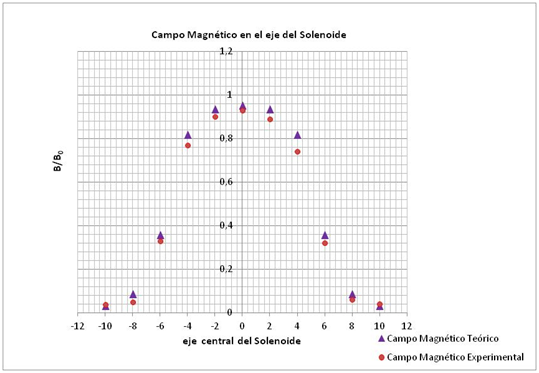
a lo largo del eje del Solenoide.
(Elaborado por @lorenzor en Microsoft Excel)
Conclusiones
Las representaciones gráficas muestran, en cada uno de los casos analizados, pequeñas discrepancias entre los valores teóricos de campo magnético y los valores de campo obtenidos por el Teslámetro, validando de esta forma lo postulado por Biot y Savart .
Es importante destacar que las predicciones arrojadas por el modelo teórico, en cuanto a la uniformidad en intensidad del campo magnético en la región interna del solenoide y en el espacio entre las bobinas de Helmholtz, está en perfecta concordancia con las mediciones experimentales.
Espero que este trabajo contribuya a fortalecer tus conocimientos sobre el electromagnetismo. Cualquier duda, pregunta, sugerencia o comentario que tengas serán bienvenidas y con mucho gusto las responderé.
Gracias por leer mi publicación.
Referencias
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Electrodinámica Clásica Segunda Edición / John David Jackson
- Electromagnetismo Conceptos y Aplicaciones Cuarta Edición / Stanley V. Marshall, Richard E. DuBroff, Gabriel G. Skitek
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo II. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 2. Addison Wesley Longman.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias por el apoyo.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Mi agradecimiento por el apoyo recibido.
Saludos @lorenzor, con esos instrumentos es ventajoso hacer las medidas del campo magnético en las diferentes bobinas que se muestran en la figura. Muy didáctico y experimental tu trabajo.
Saludos. gracias por tu visita y apoyo.
Excelente disertación la que presentas, mi amigo y colega @lorenzor, acerca de la muy importante Ley de Biot-Savart, se muestra claramente su validez mediante la experimentación que nos muestras. Disfruté su lectura, muy bien ilustrado. Saludos.
Saludos @tsoldovieri. Gracias por el apoyo.
Congratulations @lorenzor! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard: