¡Hola amigos de Steemit!
Reciban un cordial saludo.
El concepto de cantidad de movimiento o momento lineal es uno de los parámetros cuyas aplicaciones han permitido comprender y resolver una gran cantidad de fenómenos físicos clásicos, electromagnéticos, cuánticos y relativistas.
De la misma forma que el concepto de energía y su principio de conservación han permitido resolver una gran variedad de problemas físicos, el concepto de cantidad de movimiento y su principio de conservación han sido una herramienta fundamental en la solución de problemas, donde el principio de conservación de la energía resulta insuficiente o no es aplicable.
Dada su importancia, en este articulo analizaremos y ampliaremos el concepto de cantidad de movimiento mas allá de la visión clásica de este parámetro y abordaremos uno de los fenómenos donde la generalización y aplicación de este concepto jugó un papel fundamental en el discernimiento del carácter corpuscular de una onda electromagnética, el cual es conocido como la dispersión de rayos X o Efecto Compton en honor al célebre científico
Arthur Holly Compton .
 Figura 1 – Arthur Holly Compton (1892 – 1962)
Figura 1 – Arthur Holly Compton (1892 – 1962)
Wikimedia Commons - Dominio Público
Fundamentos teóricos
Desde el punto de vista clásico la cantidad de movimiento de un objeto de masa “
m” el cual se mueve a una velocidad
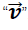
, está asociada a la dificultad de llevar dicho objeto al reposo.
Por definición la cantidad de movimiento está dada por la expresión:
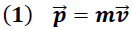
En mi artículo
Demostración experimental del principio de conservación de la cantidad de movimiento lineal (PCCML) y angular (PCCMA) (Péndulo balístico), se analizó el caso de una masa variable donde la segunda Ley de Newton es expresada necesariamente en forma general en función de la variación de la cantidad de movimiento, según lo expresa la siguiente ecuación:
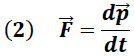
La cantidad de movimiento de un sistema también está relacionada de manera directa con la energía cinética
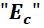
de un cuerpo, según lo expresan las siguientes ecuaciones:
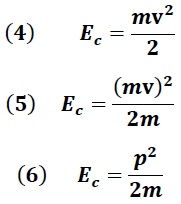
Es notorio que el movimiento de un objeto de masa “m” transmite su momento lineal de un punto a otro y por tanto su energía.
Ahora bien,
¿Qué ocurre con una onda electromagnética?
¿Tiene una onda electromagnética cantidad de movimiento?
Una de las características de las ondas electromagnéticas es la transferencia de energía, lo cual nos lleva a inferir que poseen una cantidad de movimiento.
En la siguiente figura se ilustra el caso donde una onda electromagnética transfiere cantidad de movimiento a un conductor ubicado sobre rieles aislantes.
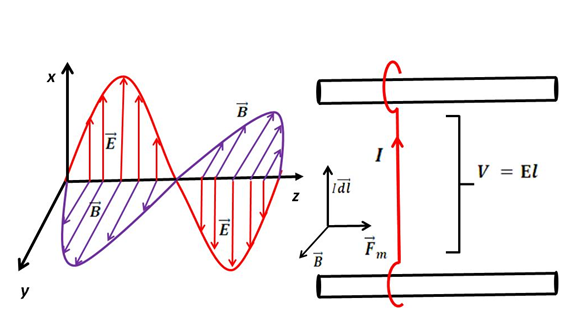 Figura 2 – Modelo esquemático de la transferencia de la cantidad de movimiento
Figura 2 – Modelo esquemático de la transferencia de la cantidad de movimiento
de una onda electromagnética a un conductor de longitud “l”
(Elaborado por @lorenzor en PowerPoint)
Las cargas eléctricas en el conductor son aceleradas por la componente eléctrica de la onda, estableciendo en este una corriente eléctrica "I" dada por la expresión:
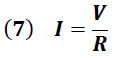
Donde “R" representa la resistencia y "V" la diferencia de potencial en el conductor definida por la siguiente expresión:
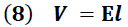
E → Campo eléctrico
l → longitud del elemento
Sustituyendo (8) en (7) se obtiene:
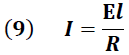
De acuerdo al Efecto Joule esta energía es disipada por el conductor con una potencia "P", dada por la expresión:
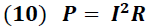
Según lo establece el principio de conservación, con la misma rapidez que la onda suministra energía al conductor esta energía es disipada, lo que permite el siguiente planteamiento:
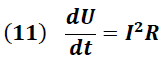
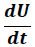 → Variación de la energía
→ Variación de la energía
Sustituyendo (9) en (11) se obtiene:
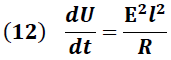
Ahora bien, la corriente eléctrica en el conductor es afectada por el campo magnético "
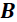
" de la onda, provocando una fuerza magnética "
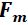
" cuya magnitud es dada por la siguiente ecuación:
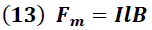
Sustituyendo (9) en (13) se obtiene:
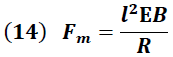
La fuerza magnética dada por la ecuación (14) es la que imparte la cantidad de movimiento transferida por la onda a dicho elemento, lo que permite escribir la segunda Ley de Newton de la siguiente forma:
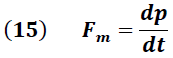
Igualando (14) y (15) obtenemos:
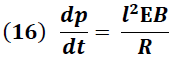
Según las ecuaciones de Maxwell el campo eléctrico y magnético están relacionados según la expresión:
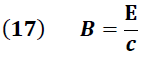
Por integración se obtiene:
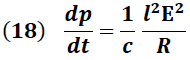
De la ecuación (12) se tiene:
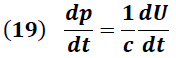
Sustituyendo (17) en (16) obtenemos:
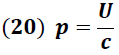
Este resultado pone de manifiesto que la onda electromagnética además de transferir energía al elemento conductor, transfiere una cantidad de movimiento la cual es gobernada por la expresión (20).
Cantidad de movimiento relativista
Otro caso de relevancia de la cantidad de movimiento ocurre en partículas que se mueven a velocidades cercanas a la velocidad de la luz
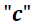
.
En este caso la cantidad de movimiento debe ser redefinido en términos relativistas según lo expresa la siguiente ecuación:
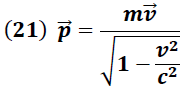
En esta expresión se observa que para partículas que se desplazan a bajas velocidades el término:
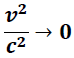
Lo cual nos conduce al caso clásico conocido de que 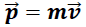 .
.
Esta nueva definición de la cantidad de movimiento nos obliga a reescribir la segunda Ley de Newton en términos relativistas de la forma:
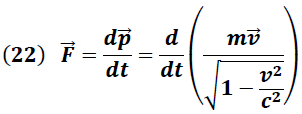
Esta definición relativista de la fuerza exige además replantear la energía cinética de forma distinta a la conocida en la mecánica Newtoniana.
La energía cinética adquirida por una partícula, cuando una fuerza actúa sobre esta, incrementa su velocidad desde el reposo
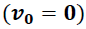
a un valor "
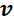
" y está dada por la expresión:
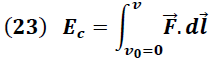
La integral de la expresión (22) conduce a la ecuación:
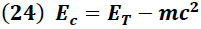
Donde "
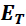
" representa la energía total de la partícula y está dada por la ecuación:
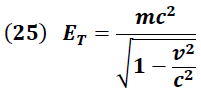
Usualmente la energía total es expresada en función de la cantidad de movimiento de la partícula, lo cual se logra combinando las expresiones (25) y (21) obteniendo:
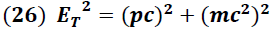
En esta ecuación es importante destacar que aunque la partícula no se encuentre en movimiento
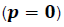
su energía esta dada por "
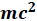
" y para partículas cuyas masas en reposo sean nula (fotón) su energía está determinada por el termino "
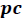
", lo cual indica que poseen, pese a su ausencia de masa, una cantidad de movimiento.
Efecto Compton
El concepto de cantidad de movimiento que hemos ampliado en este desarrollo ha permitido el análisis de modelos y fenómenos físicos donde los conceptos clásicos han resultado contradictorios.
La dualidad onda–partícula fue uno de los eventos más controversiales que por años ocupo la atención de los más grandes científicos que la física ha conocido.
Este evento fue dilucidado por el conocido Efecto Compton en el cual se demuestra teórica y experimentalmente el carácter corpuscular de una radiación electromagnética a partir de la dispersión que experimentan los rayos X, debido a su colisión con electrones.
Según la física clásica la luz y todas las ondas electromagnéticas presentan un comportamiento estrictamente ondulatorio.
Diversos experimentos realizados por prominentes científicos, tales como
Thomas Young,
Augustin Fresnel y la teoría ondulatoria del
Maxwell corroboraron el comportamiento ondulatorio de una onda.
Si bien es el efecto fotoeléctrico realizado por el gran Albert Einstein quien sienta las bases del carácter corpuscular de una onda electromagnética (luz), el Efecto Compton ratifica de forma determinante dicho comportamiento.
La demostración de Compton tiene sus cimientos en el breve desarrollo teórico que hemos expuesto sobre la cantidad de movimiento tal y como veremos más adelante.
Clásicamente una onda electromagnética incidente sobre un material hará oscilar las cargas libres presentes en este, provocando la radiación de ondas electromagnéticas con valores idénticos de frecuencia y longitud de onda.
En sus experimentos Compton observó que cuando sobre un material incide una onda electromagnética (rayos X), la onda dispersada mostraba variaciones de frecuencia y un incremento longitud de onda que no se correspondían con el modelo clásico.
Para explicar sus resultados Compton consideró que la onda electromagnética incidente (rayos X) estaba constituida por cuantos o fotones tal y como lo había propuesto Albert Einstein en su explicación del efecto fotoeléctrico en la que cada fotón tiene asociada una energía dada por la siguiente expresión:
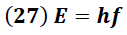
h → constante de Planck = 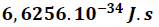
f → frecuencia de la onda
Según Compton, la energía absorbida en el impacto por el electrón se traducía en un fotón dispersado con menor nivel de energía, y según lo plantea la ecuación (27) con un valor más bajo de frecuencia y un incremento en la longitud de onda.
En la siguiente imagen se ilustra el modelo corpuscular utilizado por Compton para explicar el fenómeno de dispersión de la onda.
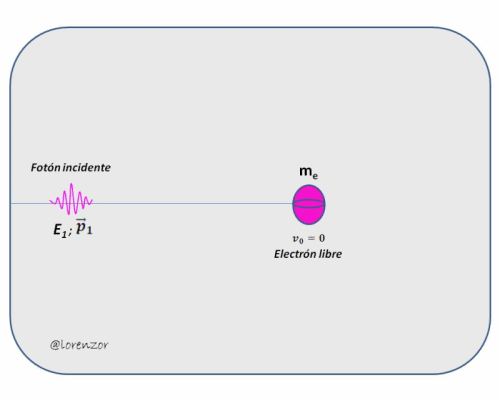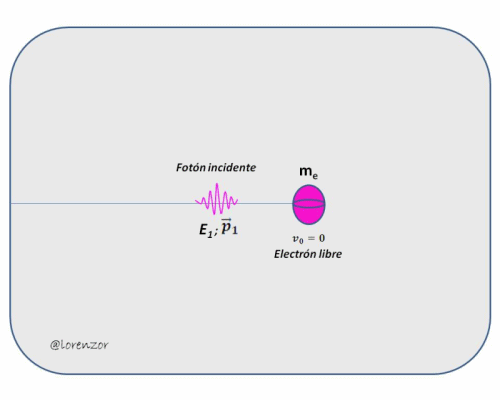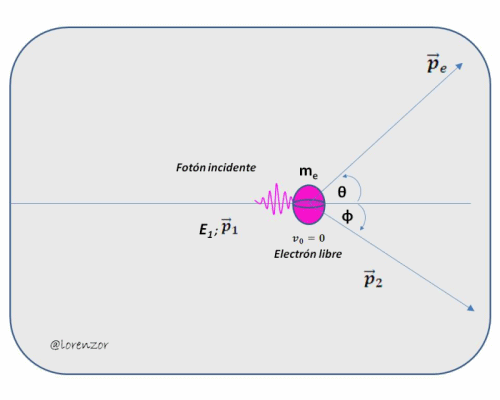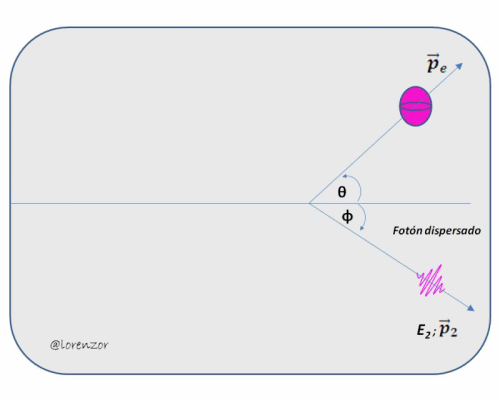 Figura 3 - Modelo esquemático de la dispersión de rayos X (Efecto Compton)
Figura 3 - Modelo esquemático de la dispersión de rayos X (Efecto Compton)
(Gif elaborado por @lorenzor en PowerPoint y PhotoScape)
Según el principio de conservación de la energía se debe cumplir que:
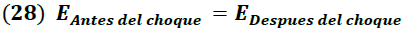
Antes del impacto, las energías a considerar son la energía del fotón incidente y la energía del electrón en reposo, las cuales están definidas por la expresión (26).
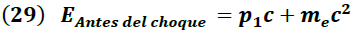
p1 → Cantidad de movimiento del fotón incidente
me → Masa del electrón
Después del impacto las energías del fotón dispersado y el electrón en retroceso están gobernadas por la expresión:
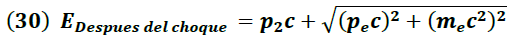
p2 → Cantidad de movimiento del fotón dispersado
pe → Cantidad de movimiento del electrón en retroceso
Igualando (29) y (30) obtenemos:
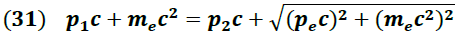
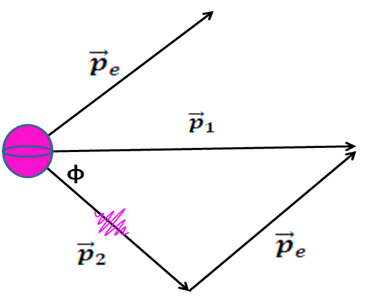 Figura 4 – Diagrama vectorial de la cantidad de movimiento del fotón y el electrón antes y después del choque
Figura 4 – Diagrama vectorial de la cantidad de movimiento del fotón y el electrón antes y después del choque
(Elaborado por @lorenzor en PowerPoint)
Según el diagrama vectorial de la figura 4 la cantidad de movimiento del electrón después del impacto puede relacionarse con las cantidades de movimiento del fotón antes y después de la colisión a través de la ley del coseno, según se expresa en la siguiente ecuación:
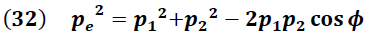
ϕ → ángulo de dispersión de rayos X
De la sustitución de (32) en (31) se obtiene:
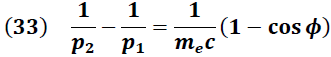
Donde tal y como se observó en el fundamento teórico, las energías de la radiación incidente y dispersada están dadas por las siguientes expresiones:
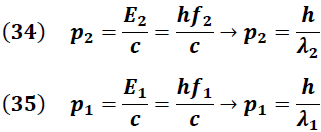
Sustituyendo (34) y (35) en (33) se obtiene la conocida Ecuación de Compton.
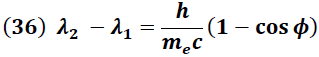
La ecuación de Compton muestra que la variación que experimenta la longitud de la onda dispersada tiene únicamente dependencia con el ángulo de dispersión "
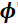
".
Es importante destacar que en este modelo los fotones de rayos X colisionan con electrones libres o electrones ligados que presentan una energía de enlace menor a la energía cedida en el impacto por los fotones de rayos X.
La concordancia entre los resultados experimentales y los obtenidos a partir de la Ecuación de Compton permitieron de forma contundente validar, bajo los principios energéticos asociados a las cantidades de movimientos aquí expuestos, el concepto de fotón y el carácter corpuscular de una onda electromagnética.
Espero que este trabajo sea de su utilidad y permita fortalecer sus conocimientos sobre la cantidad de movimiento y el impacto que este parámetro ha tenido en el estudio de importantes fenómenos físicos, como lo es el Efecto Compton. Si tienen alguna pregunta, duda o sugerencia, dejen sus comentarios y con mucho gusto les responderé.
Gracias por leer mi publicación.
Referencias
- Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 2: Electricidad y magnetismo. Luz. Física moderna. 5a edición. Editorial Reverté.
- Física. Vol. II Campos y Ondas. Marcelo Alonso, Edward J. Finn, Carlos Alberto Heras, José A. Barreto Araujo. Fondo educativo Interamericano, S.A.
- Introducción a la teoría especial de la relatividad. Robert Resnick. Editorial Limusa, México.
- Física para Ciencias e Ingeniería. Vol. 1, primera edición. John P. McKelvey, Howard Grotch. Editorial Harla, México.

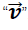 , está asociada a la dificultad de llevar dicho objeto al reposo.
, está asociada a la dificultad de llevar dicho objeto al reposo.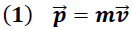
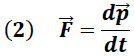
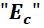 de un cuerpo, según lo expresan las siguientes ecuaciones:
de un cuerpo, según lo expresan las siguientes ecuaciones: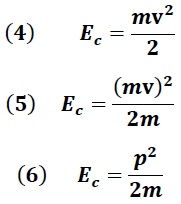

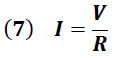
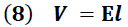
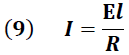
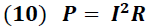
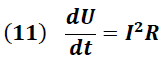
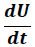 → Variación de la energía
→ Variación de la energía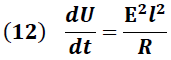
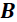 " de la onda, provocando una fuerza magnética "
" de la onda, provocando una fuerza magnética "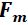 " cuya magnitud es dada por la siguiente ecuación:
" cuya magnitud es dada por la siguiente ecuación: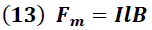
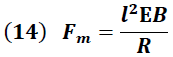
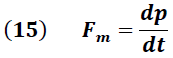
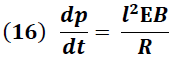
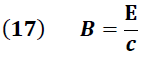
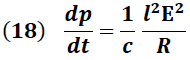
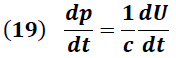
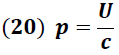
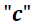 .
. 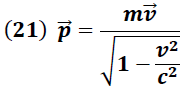
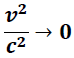
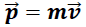 .
.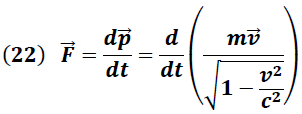
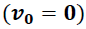 a un valor "
a un valor "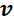 " y está dada por la expresión:
" y está dada por la expresión: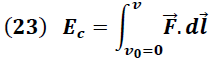
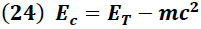
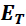 " representa la energía total de la partícula y está dada por la ecuación:
" representa la energía total de la partícula y está dada por la ecuación: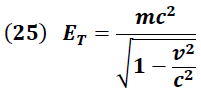
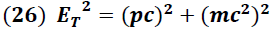
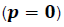 su energía esta dada por "
su energía esta dada por "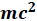 " y para partículas cuyas masas en reposo sean nula (fotón) su energía está determinada por el termino "
" y para partículas cuyas masas en reposo sean nula (fotón) su energía está determinada por el termino "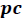 ", lo cual indica que poseen, pese a su ausencia de masa, una cantidad de movimiento.
", lo cual indica que poseen, pese a su ausencia de masa, una cantidad de movimiento.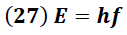
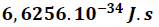

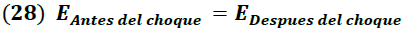
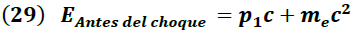
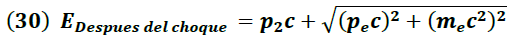
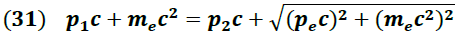

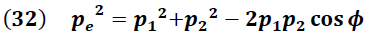
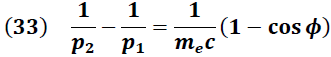
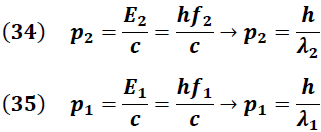
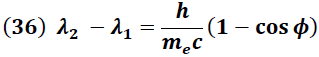
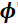 ".
".
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias por el apoyo.
Me gusto, el termino h en la ecuación 34 y 35 es la constante de planck.
Y el divisor es que? logitud de onda o frecuencia?
Las magnitudes cambian de kg m/s a otras mas complejas me imagino?
SALUTATIONS DU VENEZUELA
saludos @soy-venezuelien. Gracias por tu visita. Si efectivamente el divisor en las ecuaciones 34 y 35 representan las longitudes de onda respectivas. En la ecuación siguiente(36) lo manifiesto como la variación de las longitudes de onda. Respecto a las unidades estas permanecen invariantes , son expresadas en Kg m/s en cualquiera de los casos. En el caso de la cantidad de movimiento de una onda puedes ver que:
Espero haberte ayudado a disipar tu duda. Gracias por tu interés y tu tiempo.
Buen post, profesor @Lorenzor! Por cierto, quiero comentarle - a manera de aporte- que tiene algunas tildes (acentos) por aplicar 😉 Es algo que siempre mejora la presentación de los artículos y es necesario para #STEM-Espanol. Buen contenido! Saludos
¡Saludos @eniolw!, muchas gracias por tu comentario. Ya las correcciones respecto a las tildes que se me escaparon fueron realizadas.
Agradezco tu aporte en pro de mejorar los contenidos compartidos en la comunidad de @stem-espanol.
Muy excelente su post profe @lorenzor. Pienso que esta teoría posee múltiples aplicaciones. Estos conceptos prácticamente unen dos partes fundamentales de la física, la teoría electromagnética y la teoría relativista. No conozco mucho acerca de este tema, pero estoy sumamente complacido de contar con sus conocimientos en Física para #stem-espanol.
Un saludo.
¡Saludos @djredimi2!. Gracias por tu comentario positivo. Complacido que la información que he compartido te resulte interesante y de utilidad.
Buenas tardes @lorenzor, buen trabajo y didáctico para explicar las clases. Como se asocia la ley de Ohm y el efecto de Compton.
saludos estimado @germanmontero. Gracias por su apoyo y comentario.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Mi agradecimiento por el apoyo recibido.
Excelente post sobre el Efecto Compton y su relación con la Cantidad de Movimiento Lineal amigo y colega @lorenzor. Votado y reestimeado. Gracias por compartirlo. Saludos.
gracias mi estimado amigo. Siempre es un honor tenerlo de visita por aquí.
Excelente publicación Prof. Lorenzo. Por fin entendí el efecto Compton gracias a este post :).