MISTERIOS MAGNÉTICOS 4
Dipolos magnéticos e interacción dipolar
Hola a todos, apreciados colegas y amigos de STEEMIT. De nuevo trayéndoles lo más destacado de mis archivos de Física Básica, en este caso el magnetismo. En Capítulos anteriores de la serie “Misterios Magnéticos” hemos estado discutiendo temas de nuestra vida donde el magnetismo es pilar fundamental. Entre estos hemos discutido temas tales como la rotación de La Tierra, las leyes de la magnetostática, polos magnéticos, la brújula, péndulos magnéticos, entre otros. Si te has perdido ésta Serie te invito a viajar por los enlaces:
Debo decirles que cada experimento o demostración que a Uds. les presento, los muestro a mis Estudiantes de Ingeniería. Para este Capítulo de “Misterios Magnéticos” me inspiré en una clase de “Electromagnetismo”, donde intentaba explicar el origen del magnetismo y cómo este se propaga en la materia. Surgieron las preguntas:
El magnetismo es un efecto invisible ante nuestros sentidos: no podemos sentir el efecto de un campo magnético, pero si vemos sus efectos en los objetos macroscópicos. Para responder estas preguntas debemos utilizar unas capacidades de observación y experimentar un poco. Te mostraré que podemos resolver problemas científicos de nuestro entorno sin equipamientos complejos y costosos y sin tener gran experiencia en física. En este trabajo te propongo un paseo a través del magnetismo y “ver” algunos de sus efectos.
Con la finalidad de hacer este proyecto más interactivo, les agradezco dejarme sus inquietudes y preguntas en un REPLAY, y así darles respuesta.
Para más información sobre este tema y otros relacionados con Ciencia, Física y Tecnología, les invito visitar mis sitios:
Dipolo magnético. Campo dipolar.
Fue Ampère quien primero idealizó la estructura de un material magnético y el porqué la materia puede producir campos magnéticos. Para esto, introdujo el concepto de momento magnético,

A es el área del circuito, I la corriente y n el vector normal al plano del circuito. Entonces según Ampère todo material magnético estaba constituido por pequeñas corrientes cerradas, como se muestra en la Figura 1.
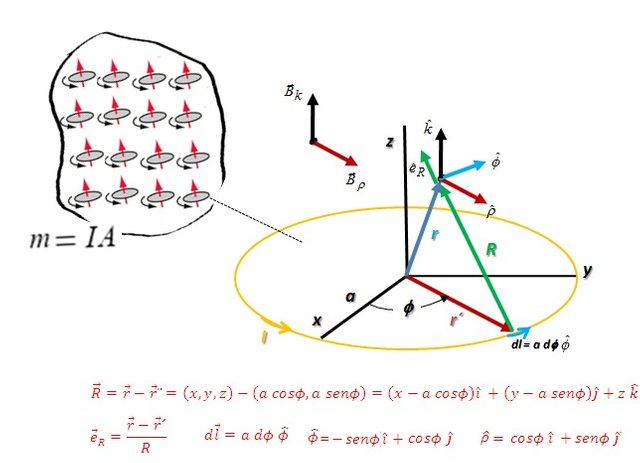
Figura 1. Geometría típica para describir un dipolo magnético (Propiedad del Autor)
Cada una de estas corrientes cerradas o espiras de corriente generan un campo magnético en cualquier punto fuera del eje, B, dado por la Ley de Biot-Savart,

donde μ es la permeabilidad magnética del medio. Considerando la configuración de la Figura 1, tenemos,
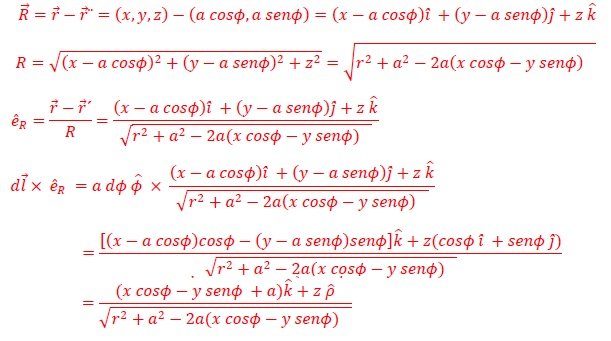
Con esto, el campo magnético es obtenido a partir de la Ecuación (2) y está determinado por la integral,
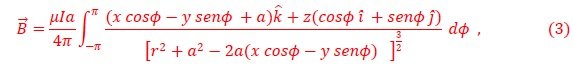


Estas integrales son en general complicadas de resolver ya que involucran integrales elípticas de primera y segunda clase. En vez de realizar cálculos explícitos, nuestro interés se centrará en entender la fenomenología de la interacción dipolar.
En el caso particular del campo en el eje de la espira (Bx=By=0; x=y = 0, r = z), obtenemos,

Interacción entre dipolos Amperianos. Corrientes de magnetización
Considera dos dipolos “Amperianos” como los de la Figura 2. La interacción entre estos dos dipolos magnéticos viene dada por la conocida Ley de Ampére,

donde I2 es la corriente de la espira № 2 de longitud l2, y B1 es el campo producido por la espira № 1 expresado en las Ecuaciones (4)-(5) y (6). Utilizando el diferencial de l2 de la espira № 2,

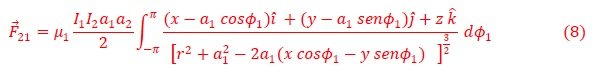
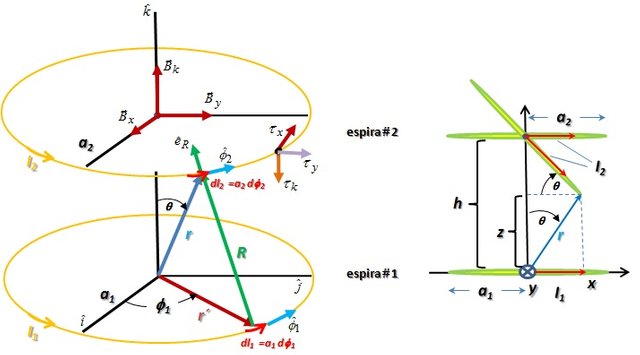
Figura 2. Interacción dipolar entre dos dipolos magnéticos Amperianos (Propiedad del Autor).
Al igual que en el caso del campo magnético de la espira simple, esta integral también requiere resolver funciones elípticas de primera y segunda clase. Sin embargo, desde el punto de vista fenomenológico esta fuerza produce un torque entre las espiras dado por la ecuación vectorial,


donde las componentes de la fuerza están explícitamente determinadas en la integral (8). Introduciendo las correspondientes componentes de (8) en (10), obtenemos que las componentes del torque se reducen a,

La fuerza de interacción induce torques en el plano de las espiras y en la dirección vertical, como se muestra en la Figura 2. Este es un movimiento compuesto por una rotación alrededor del eje de las espiras y una nutación con eje de oscilación a lo largo del radio. Debido a este movimiento de nutación, el plano de la espira № 2 se inclina con respecto al plano de la espira № 1 en un ángulo θ, tal en la configuración de la Figura 2. Si las espiras están separadas una distancia h, entonces tenemos que el torque sobre la espira № 2 es,

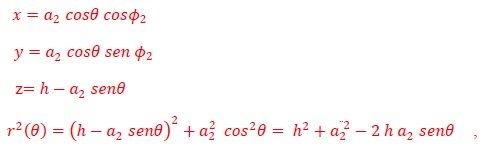
en las Ecuaciones del torque dadas en (11). Si las corrientes están en fase (ф1=ф2), entonces τz(θ)=0 y solo existirá un torque en el plano XY equivalente a una rotación alrededor del eje de las espiras. Se requiere que las corrientes estén desfasadas para que el plano de las espiras se incline con respecto a la horizontal, y producir en consecuencia una nutación del eje de la espira.
El modelo descrito no solo es válido para distribuciones homogéneas de corriente, como por ejemplo, una corriente de cargas fluyendo a través de una espira de cobre, sino también cuando las espiras están compuestas de un material magnetizable, tal como un alambre de hierro o cualquier otro material ferromagnético. Sin embargo, debido a la esencia estructural de la materia el campo producido por ésta es paralelo a la magnetización, y es más conveniente describir el sistema a través de la Ecuación de la densidad de torque magnético,

que experimenta la magnetización M en presencia de un campo B. Ahora estudiemos la interacción dipolar entre dos espiras ferromagnéticas o magnetizadas. El torque que ejerce la espira № 1 sobre la espira № 2 es,

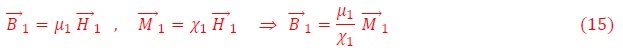

Por simetría, ambas espiras se magnetizan a lo largo del alambre, es decir, en el plano de cada espira,


Fenomenológicamente analizaremos dos casos límites con ésta ecuación: a) espiras magnéticas paralelas; b) espiras magnéticas perpendiculares. Ambos casos se esquematizan en la Figura 3. En el caso (a), se produce sobre cada espira un torque en la dirección perpendicular al plano de las espiras. Este torque induce oscilaciones periódicas con respecto a un eje de rotación en el plano de las espiras. En el caso límite (b), los planos de las espiras están colocadas perpendicularmente entre ellos. Considerando la espira № 2 a lo largo del plano XZ, tendremos,

Como se observa en la Figura 3, se induce un torque en la dirección vertical que produce una rotación de la espira № 2 alrededor de su eje, y torques en el plano horizontal XY que hacen girar el plano de la espira № 2 alrededor del eje Z. Recíprocamente, el torque que induce a espira 2 sobre la espira 1 es:

Para apreciar cómo funcionan todas estas Ecuaciones les mostraré en la próxima sección algunas demostraciones con espiras metálicas imantadas.
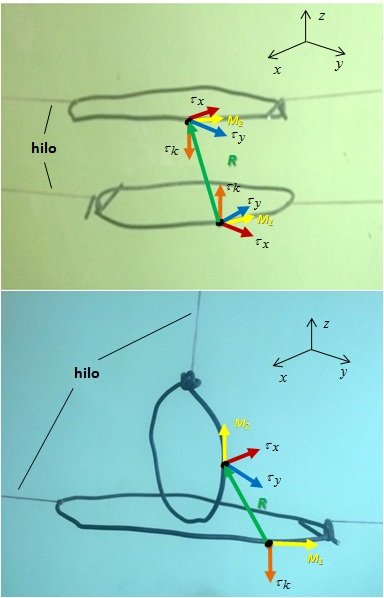
Figura 3. Configuraciones paralela y perpendicular de dos espiras magnetizadas interactuando a través de campos dipolares (Propiedad del Autor).
Demostración: interacción dipolar magnética
Materiales y procedimientos
El objetivo de ésta sección es mostrarles cómo, a pesar de la aparente complejidad algebraica de la teoría de las interacciones magnéticas, su fenomenología es muy simple. Mostraremos la esencia de la interacción entre espiras metálicas magnetizadas y sus efectos mecánicos.
Para esto necesitaremos básicamente los materiales y elementos que se muestran en la Figura 4. Luego que tengas todos los materiales a la mano, construye las estructuras como aparecen en las Figuras 5 y 6. El elemento fundamental para nuestro experimento es un dispositivo llamado “dipolo magnético múltiple”. Primero experimentaremos con el “dipolo doble” y también les presentaré mi arreglo múltiple de más de dos (2) espiras. Estos son montajes para fines didácticos que nos permiten visualizar la interacción magnética dipolar.

Figura 4. Materiales utilizados en los experimentos propuestos en este trabajo (Propiedad del Autor).
1) Imantar los alambres frotándolos varias veces con el imán. Para saber si el alambre está magnetizado acércalo a la brújula. Si la aguja se mueve el alambre se magnetizó.
2) Construir varias espiras doblando el alambre utilizando como molde un vaso o algún objeto cilíndrico o esférico.
3) Clavar los clavos en los palos de madera equi-distantemente, a una distancia igual al diámetro de las espiras.
4) Rellena los envases de refresco con agua y luego inserta los palos de madera hasta unos 15-20 cm. Esto es para estabilizar el peso de la estructura y evitar vibraciones indeseadas.
4) Ata con el hilo tus espiras a los clavos de ambos palos de madera. Tensa los hilos cuidando que las espiras tengan sus planos lo más horizontal posible.
5) El plano de apoyo horizontal debe estar nivelado. Para esto usa un nivel de agua.
6) También puedes experimentar con dipolos de variadas geometrías y formas.
7) Para que te familiarices con el funcionamiento del dispositivo, prueba primero con un espira, luego con dos espiras, etc.

Figura 5. Elementos básicos para construir estructuras multipolares magnéticas (Propiedad del Autor).

Figura 6. Estructuras multipolares magnéticas terminadas (Propiedad del Autor).
Comentarios finales
Las fuerzas magnéticas son efectos invisibles e indetectables para nuestros sentidos, produciendo fenómenos incomprensibles para nosotros. Sin embargo, estamos inmersos en un mar de ondas y campos magnéticos. Gracias a las fuerzas y campos magnéticos, la materia permanece unida debido a la interacción entre los dipolos magnéticos que la conforman, formando materiales de diversa índole: diamagnéticos, paramagnéticos, ferromagnéticos, antiferromagnéticos, ferrimagnéticos, entre muchos otros.
Los campos y fuerzas magnéticas no son solo producto de las cargas en movimiento, o corrientes eléctricas. La materia magnetizable, tal como un alambre de hierro está constituida por dipolos magnéticos diminutos que interaccionan entre sí, generando torques entre los átomos. Estos torques inducen rotaciones en los planos principales del dipolo.
Sin torques magnéticos nuestro planeta no podría rotar alrededor de sobre su propio eje ni trasladarse alrededor del Sol, y por lo tanto no existirían el día y noche, o los meses y los años. Tendríamos un planeta sobrecalentado en un lado y sobre enfriado en el otro: no existiría la vida en el planeta.
Con demostraciones sencillas estudiamos la dinámica de estos péndulos, y pudimos reproducir el movimiento de un planeta alrededor del Sol.
Antes de despedirme, me gustaría llamar la atención de la comunidad de docentes tanto a nivel medio como universitario, para que consideren incorporar en sus actividades docentes la discusión de estos problemas cotidianos, donde las leyes y principios de la física son la base fundamental.
Agadecimiento
Quiero agradecer de manera especial a la STEEMER @viagaby, por su valiosa colaboración en la edición de los videos de este artículo y los anteriores. Colaboración sin la cual no sería posible este proyecto.
Lecturas sugeridas sobre magnetismo y materiales magnéticos:
1. E. W. Lee, Magnetism: an introductory survey, DOVER Pub. Inc, NY (1970).
2. Guillermo Heyaca Verela, Energía de los Campos Magnéticos, Eds. Nueva Librería, Buenos Aires (1980).
3. Nicola Spaldin, Magnetic Materials: Fundamentals and Device Applications, Cambrigde University Press (2003)
4. Rebecca Carmi, Amazing Magnetism: Magic School Bus Chapter # 12, Scholastic Inc. (2001)
5. John David Jackson, Classical Electrodynamics, 2nd Edition, Willey-Sons, NY (1975)
6. Edward M. Purcell, Electricidad y Magnetismo, Berkeley Physics Course, Ed. Reverté, Madrid (1980)
7. Charles Kittel, Introduction to Solid State Physics, 6th Ed., Wiley-Sons, NY (1986)
Great post. It doesn't seem like you are getting the likes it deserves though. Have you checked out the upvote communities? You should check out steemengine. or steemfollower.com.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Hola @jfermin70. Interesante práctica para realizar con los estudiantes con materiales sencillos de conseguir, y conseguir de forma didáctica como explicar la interacción magnética dipolar. Como lo señalas son efectos invisibles para nuestros sentidos, pero estamos rodeados de ese campos magnéticos. Gracias por compartir esta información. Saludo.
Congratulations @jfermin70! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!