ACELERACIÓN DE CUERPOS RODANTES SOBRE UN PLANO INCLINADO
ACELERACIÓN DE CUERPOS RODANTES SOBRE UN PLANO INCLINADO
INTRODUCCIÓN
Cuando un cuerpo esférico o cilíndrico rueda sin deslizar por una superficie inclinada, sus puntos de contactos con la superficie están momentáneamente en reposo y el objeto gira respecto a un eje de rotación que pasa por medio del punto de contacto. En virtud de que la fuerza de rozamiento entre el plano y el cuerpo sólo actúa en los puntos de contacto, la fuerza de roce no produce trabajo por lo que se conserva la energía mecánica.
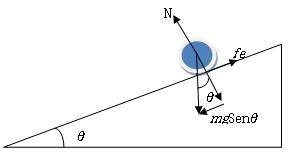
Figura 1. Diagrama esquemático de las fuerzas que actúan en un cuerpo rodante
En la figura 1, se muestra un plano inclinado de una superficie plana que forma un ángulo agudo con la horizontal y encima de él se encuentra una esfera maciza de radio R y masa m que rueda sin deslizar por su superficie.
Por otro lado, según la Segunda Ley de Newton, la aceleración del centro de masas es igual a la fuerza neta dividida por la masa. Las fuerzas que actúan sobre la esfera son el peso, la fuerza normal que equilibra la componente vertical del peso, y la fuerza de roce de naturaleza estática actúa hacia arriba del plano inclinado. Cuando el objeto acelera por el plano, para que no se deslice, su velocidad angular tiene que aumentar, por lo que se requiere un momento externo neto alrededor del eje que pasa por su centro de masas.
Aplicando la segunda ley de Newton a lo largo del eje x se tiene:
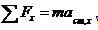 (1)
(1)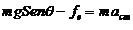 (2)
(2)De la misma manera, aplicando la Segunda Ley de Newton al movimiento de rotación, tomando en cuenta la rotación alrededor de un eje paralelo al eje instantáneo de rotación y que pasa por su centro de masas, se tiene que:
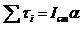 (3)
(3)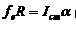 (4)
(4) De la relación de y tomando en consideración la ausencia de deslizamiento se tiene:
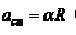 (5)
(5)Ahora bien, resolviendo estas ecuaciones llegamos al siguiente resultado:
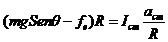 (6)
(6)Por lo tanto, la aceleración del centro de masas será:
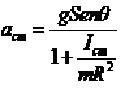 (7)
(7) Para una esfera sólida, , por lo que la aceleración del centro de masas para este sólido es:
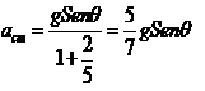 (8)
(8) Según [1], en general para un cuerpo que rueda sin deslizar, la aceleración de su centro de masas está dado por:
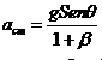 (9)
(9) Donde, 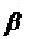 es un valor que depende de la geometría del sólido, e indica que el cuerpo que tenga menor éste, llegará primero. Es decir, la aceleración es mayor. Para una esfera 2/5 se tiene el valor es 1/2 y para un cilindro .
es un valor que depende de la geometría del sólido, e indica que el cuerpo que tenga menor éste, llegará primero. Es decir, la aceleración es mayor. Para una esfera 2/5 se tiene el valor es 1/2 y para un cilindro .
MÉTODO EXPERIMENTAL
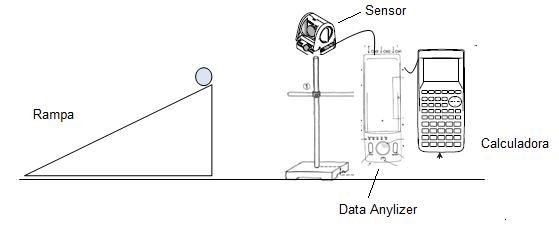
La experiencia consistió en medir la aceleración del centro de masa de cuerpos sólidos (esfera solida y cilindro solido), que ruedan sin deslizar sobre un plano inclinado, a un ángulo de 30° con la horizontal. Para esta prueba se dispuso de un sensor de movimiento ubicado a 60 cm del objeto a medir. Este sensor esta a su vez está conectado a una interface (Data Analyzer EA-200) y a una calculadora gráfica Casio Class Pad 300 Plus.
Una vez conectado el sistema como se muestra en la Figura 2, se comienza a tomar las medidas con el empleo del programa Econ 200 que se encuentra en la calculadora. Los datos obtenidos para los diferentes cuerpos rodantes se grafican instantáneamente en la calculadora almacenando los datos, que posteriormente serán procesados en un programa de análisis de datos y graficas Microcal Origin9 versión 8.01.
RESULTADOS OBTENIDOS
Los resultados se obtuvieron midiendo las aceleraciones de los cuerpos de diferentes cuerpos rodantes en nuestro caso: el cilindro macizo y la esfera, para la cual, se siguió la metodología experimental descrita anteriormente.
La gráfica 1, muestra la distancia recorrida por el cilindro macizo en función del tiempo. El valor para la aceleración que adquiere este cuerpo se presenta en la tabla 1.
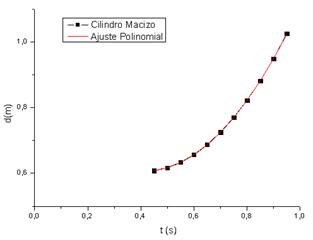
De la misma manera, la gráfica de la posición versus el tiempo para la esfera maciza que rueda sin deslizar a través del plano inclinado, se presenta en la tabla 1.
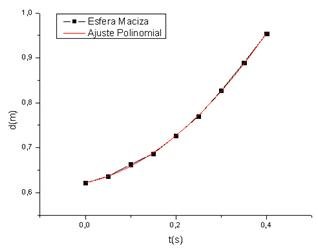 .
.Tabla 1. Aceleración de diferentes cuerpos que ruedan sin deslizar por un plano inclinado 30º con la horizontal.
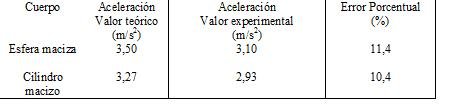
El cálculo de las aceleraciones están explicadas con detalles en los post anteriores:
Coeficiente de fricción en un sistema dinámico
ESTUDIO DE LA CAÍDA LIBRE UTILIZANDO DIFERENTES MÉTODOS EXPERIMENTALES
ESTUDIO DE LA CAÍDA LIBRE UTILIZANDO DIFERENTES MÉTODOS EXPERIMENTALES (SEGUNDA FASE)
CONCLUSIONES
En esta experiencia se ha corroborado el comportamiento parabólico de la gráfica posición versus tiempo de cuerpos rígidos que ruedan sin deslizar por un plano inclinado. Se observó que el cilindro tarda más en recorrer el plano, comparado con la esfera y corroborando los argumentos teóricos. Por otro lado, aunque los valores teóricos de las aceleraciones de los objetos estudiados están aproximadamente a un 10 % por debajo de los valores predichos, desde el punto de vista del macro mundo físico, es aceptable en virtud de que pueden jugar un factor importante, los errores sistemáticos al soltar los cuerpos de forma manual por la rampa. Por lo tanto, se sugiere repetir la experiencia automatizando el proceso de soltado de los cuerpos. Así como también la aceleración de los cuerpos depende de la distribución de la masa en los cuerpos geométricos.
Espero que les guste mi post y lo disfruten. Gracias al grupo Steemstem y steem-espanol
REFERENCIAS
1.- Calderón, S. y otros. Estudio cinemático del movimiento de cuerpos que ruedan por un plano inclinado. Lat. Am. J. Phys. Educ. Vol. 3, No. 1, Jan. 2009. http://www.journal.lapen.org.mx
2.- Tipler P., Mosca, G. Física para la Ciencia y la Tecnología. 5ta. Edición. Reverté. España, 2005.
3.- Serway, R., Beichner, R. Física para la Ciencia e Ingeniería. 5ta. Edición. McGraw-Hill. Interamericana Editores. México, 2002.
4.- Sears, F., Zemansky, M., Young, H., Freedman, R. Física Universitaria. 11a. Edición. México, 2004.
5.- CASIO, Worldwide Education Website, http://edu.casio.com/
6.- CASIO, Classpad, http://classpad.net/
7.- CASIO International, http://www.casio-intl.com/
8.- User´s Guides of the data analyzer from Casio or Texas Instruments.
9.- Originlab Data analysis and Graphing Software. www.originlab.com.
hola @germanmontero como un comentario constructivo te aconsejaria hacer los post un poco más resumidos de forma que expliques al lector y no se vuelva una lectura tediosa. saludos espero te sirva :D
Hola @arenita, gracias por tu recomendación. Aveces los post son largos y otros cortos. Mis posts anterior son un poquito largos. Este lo envie algo más resumido colocando unos link, para que el lector pueda entender la manera de calcular la aceleración.
Gracias.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Muy buena versión experimental del clásico problema del cuerpo rígido que rueda sin resbalar sobre un plano inclinado. Gracias por compartirla con todos nosotros @germanmontero. Saludos.
Saludos @germanmontero. Excelente trabajo y muy bien explicado. Mis felicitaciones.
Congratulations @germanmontero! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOP