¡Muy buen día!

Fuente

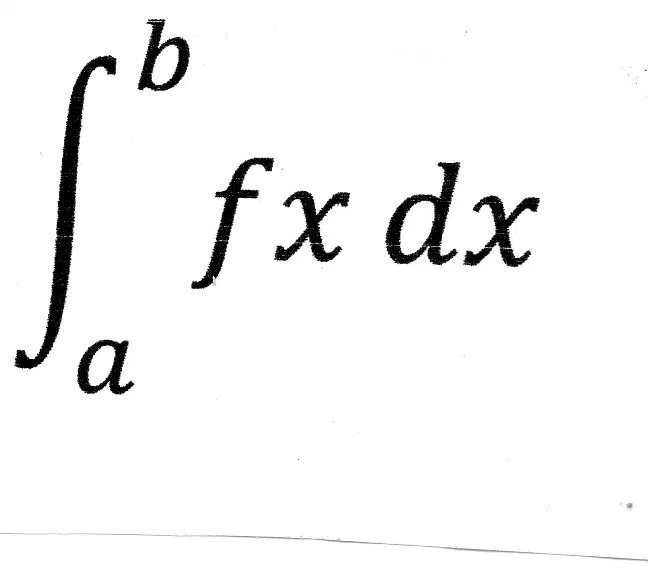
Usados estos métodos por primera vez por científicos como Isaac Newton, Arquímedes, René Descartes, el cálculo integral es una rama de las matemáticas, muy común en las ciencias e ingenierías. Estos cálculos se utilizan para los cálculos de un área y/o volúmenes de regiones.

Terminología

Si una función tiene una integral, es integrable. De su función donde se calcula la integral se le dice integrando. También, se les denomina dominio de integración a las regiones donde se integra la función, si dicha integral no tiene dominio de integración esta se convierte en integral indefinida, mientras que la integral que contenga dominio de integración es una integral definida. La integración puede tener más de una variable, y su dominio puede ser un volumen, un área, hasta un espacio abstracto sin estructura geométrica.

• Uno de sus casos más conocidos y sencillos, es la integral de función real f teniendo de variable a x y como límites (a,b), aquí su integral:

Fuente

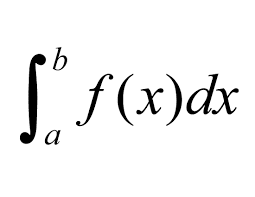
∫ representa su integración, en este caso a y b son sus límites, estos se encargan de darle una definición al dominio de la integral. Sus limites pueden variar, ya sea con números, letras, símbolos, funciones trigonométricas. Su integrando es el f, este se evalúa al variar x sobre los límites (a,b) y dx puede tomarse como muchas interpretaciones dependiendo de la teoría que se realice en la integral.

Aplicación

Las integrales suelen aparecer en varias situaciones que puedan ser practicadas con este, por ejemplo, consideremos una piscina, si esta en rectangular y su profundidad uniforme, por su longitud, anchura y profundidad podremos saber el volumen del agua que puede contener para llenar dicha piscina, el área de la superficie la cual cubre, y si se quiere saber sus medidas se determina su longitud en el borde.

Un sencillo ejemplo de como podríamos calcular algún área con este método sería el siguiente:

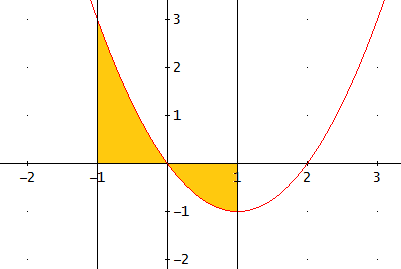
• Si su función es f(x) = x² y a = 0, b = 1, obtenemos la siguiente área de color amarillo.

Fuente

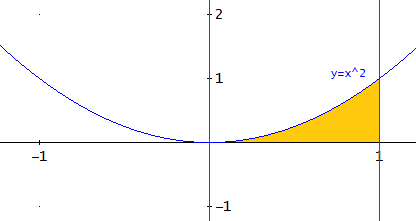
Existen varias funciones que nos ayudan a encontrar el área de otros tipos de ejercicios, entre esos tenemos:

• Áreas de dos funciones

Fuente

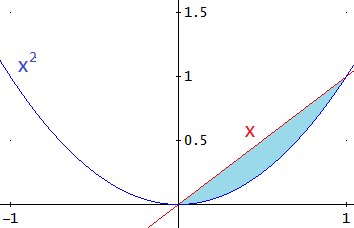
• Funciones de signos no constantes

Fuente

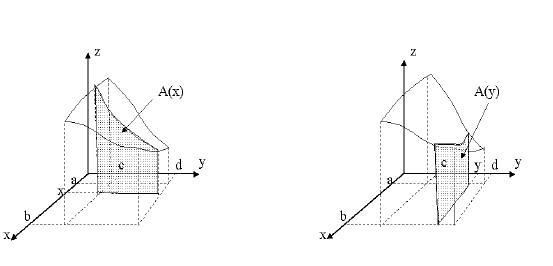
• Integrales múltiples (dobles o triples)

Fuente

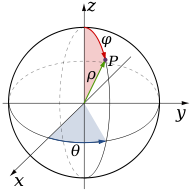
• Coordenadas esféricas

Fuente

Aplicaciones En Física

Muchas de las leyes físicas se expresan en forma de ecuaciones diferenciales. Por ejemplo, una integral puede utilizarse para resolver el problema de una caída libre de un cuerpo en la gravedad de la tierra. En la tierra, la aceleración de la gravedad se aproxima a unos g = 9,81 m/s², quiere decir que un cuerpo que comienza a caer con una velocidad nula esa velocidad viene dada por la función:

Fuente

• Su signo negativo se debe a que su gravedad es dirigida hacia el centro de la tierra, para que este fuese positiva su dirección por lógica debería de ser hacia arriba.

• Si se quisiera saber la distancia que recorrió el cuerpo s epodría razonar empleando la siguiente integral:

Fuente

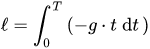
• El resultado sería el siguiente:

Fuente

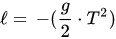
• Otros ejemplos que podrían mencionarse del uso de las integrales en la física podría ser La Energía, energía que en un tiempo es consumida es su integral de la potencia durante el tiempo consumido.

• Variaciones en cargas eléctricas de condensadores, su integral son las variaciones de la corriente eléctrica que se dirigen al condensador durante un tiempo.

Ejercicios

Cabe decir que no todos los ejercicios son de igual forma, sus limites pueden ir desde π hasta números con raíces, sus funciones desde senx, cosx, ctgx, tgx entre otros, aquí algunos ejercicios de demostración:

Fuente

Fuente

Fuente

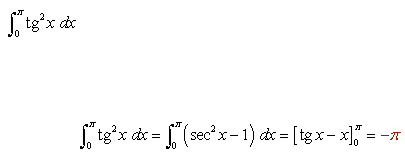
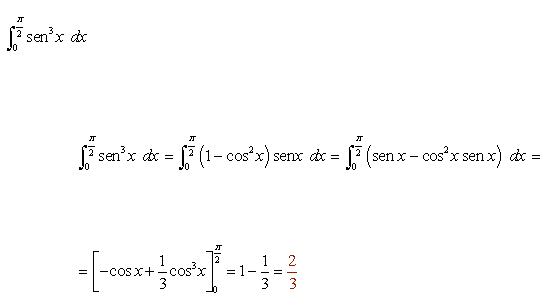
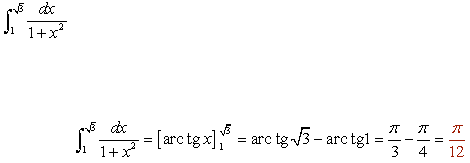
Algunas de sus integrales pueden verse aquí:

Fuente

En la mayoría de sus ejercicios, nos pedirán que derivemos nuestras integrales, aquí algunos ejemplos:

Fuente

No se aprecian la integral como tal en estos ejercicios, debido a que solo se puede observar sus derivadas, pero muy fácilmente, en una integral, su f(x) pueden ser cualquiera de estas identidades. El truco de estos ejercicios está en usar el método con el que te sientas cómodo, tener paciencia, y saber usar los artilugios para estos tipos de ejercicios, lo bueno de las matemáticas es que existen varios caminos que puedes tomar en muchos ejercicios, solo tienes que elegir el que más te guste, o el que menos sea complicado para ti.

He aquí una tabla que puede orientarte para algunas derivadas:

Fuente

Existen muchos y diferentes tipos de ejercicios de integrales, otros pueden ser confusos, otros con métodos largos y otros sencillos, otros en donde necesitarás manuales para poder terminar una integral, entre esos manuales está El Manual de Schaum u otros manuales de formulas que te permitan la finalización exitosa de tus exámenes o ejercicios.

Referencias Bibliográficas

1. Sitio web: https://es.wikipedia.org/wiki/Integraci%C3%B3n#M%C3%A9todos_y_aplicaciones

2. Sitio Web: https://www.geogebra.org/m/HzQr5MGM

3. Sitio Web: https://www.inetor.com/definidas/ejercicios_definida.html

4. Sitio Web: https://drive.google.com/drive/folders/0B56WTKMIJMvwbkpqRXRqQnY1bEE

5. Sitio Web: https://www.vitutor.com/fun/4/b_c1.html

Si te gustan los temas de este estilo por favor házmelo saber con un voto, un comentario o un reesteem, me ayudarías mucho con tu apoyo, te deseo un excelente día. ¡Gracias por leer!

Quiero darle las gracias a #stem-espanol por promover la ciencia, a la plataforma #steemit y a las personas que siempre me han apoyado desde que comencé en esta excelente red social; @hogarcosmico @rchirinos @annyclf @paolasophiat @luisrz28 @jesusrafaelmb @erika89 @rubenanez @natitips