Herramienta instruccional, basada en la Visualización mediante el uso de GeoGebra, para el aprendizaje de las funciones reales de variable real.
Hola, apreciados miembros de la comunidad científica de #CERVANTES, #STEM-EspanoL, #SteemSTEM, y STEEMIT en general, bienvenido nuevamente a mi blog. La presente publicación desarrollada por Jesse Rivero y Marilex Porteles (@xeliram) es un aporte a la comunidad educativa y todo aquel que tenga la necesidad de aprender o profundizar en el tema de funciones aquí desarrollado, contribuyendo así a mejorar la calidad de la educación en tanto que acerca al lector a un método poco utilizado como lo es la Visualización bajo un entorno computarizado. En este sentido, es importante resaltar, que las tecnologías son herramienta didácticas usadas para ayudar en el desarrollo del pensamiento, la imaginación, la socialización, entre otros, sustituyendo el método tradicional (Carrasco, 2009).
Es importante resaltar que la intención de este post no es hacer en la computadora lo mismo que se hace con lápiz y papel, se trata de mejorar la comprensión, ampliar el entendimiento de hacer las cosas de modo diferente, tal como lo señala D’Ambrósio (citado en Benedicto, 2012), si se realiza las construcciones gráficas de funciones con el computador, permitiría ampliar las posibilidades de observación e investigación, porque algunas etapas del proceso constructivo se sintetizarían.
Se espera que mediante la herramienta instruccional, basada en la visualización mediante el uso de GeoGebra para el aprendizaje del tema de funciones reales de variable real, se logre despertar el interés, generar entusiasmo y confianza en el estudiante y el lector en general.
En este post presentaremos una herramienta instruccional basada en la visualización para el aprendizaje de las funciones de variables reales, para mejorar la comprensión de algunos conceptos que tiene como objetivo la utilización del GeoGebra, dado que esta herramienta fortalece la percepción visual y geométrica de los conceptos, proporcionando con ello su comprensión. Asimismo su uso puede contribuir al aprendizaje de los estudiantes en los conceptos de funciones, permitiendo la representación de imágenes dinámicas que facilitan la visualización de los conceptos, el proceso de razonamiento y la deducción por parte del estudiante. Por su parte, Madrid (2001) señala que los software permiten cambiar la presentación de los contenidos favoreciendo la visualización y aumentando el interés por la materia, lo que hace que el GeoGebra sea eficaz en el aprendizaje de las funciones.
OBJETIVO GENERAL
OBJETIVO GENERAL
- Proporcionar un recurso didáctico basado en la visualización para el aprendizaje de las funciones de variables reales.
OBJETIVOS
ESPECÍFICOS
OBJETIVOS ESPECÍFICOS
- Proporcionar un recurso didáctico basado en la visualización para el aprendizaje de las funciones de variables reales.
- Aprovechar la visualización dinámica e interactiva que ofrece GeoGebra para comprender, profundizar y mejorar la observación y análisis de las propiedades de las funciones
La herramienta instruccional, basada en la Visualización mediante el uso de GeoGebra, para el aprendizaje de las funciones reales de variable real, se desarrollarán sólo las funciones del tipo algebraicas. La misma se desarrolla en 6 Post. La estructura de los post se presenta en el siguiente cuadro.
ESTRUCTURA DE LOS POST
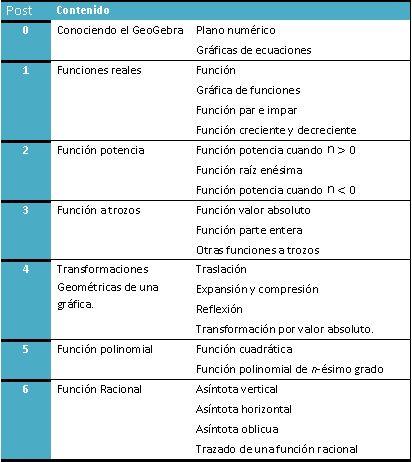
Fuente: Editada en powerPoint. Elaborada por Marilex Porteles y Jesse Rivero
Post 0
Graficando con GeoGebra
Post 0
Graficando con GeoGebra
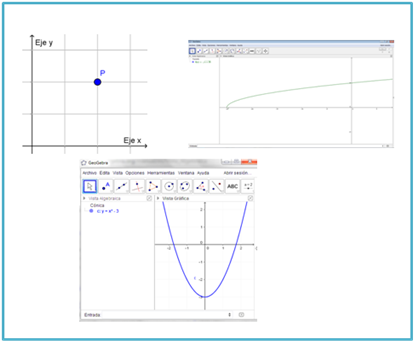
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
CONTENIDOS
- Plano numérico
- Gráficas de ecuaciones
OBJETIVOS
- Familiarizarse con el plano numérico en la interfaz de GeoGebra
- Graficar puntos en GeoGebra
- Aprender a calcular distancia entre puntos con GeoGebra
- Aprender a determinar el punto medio entre dos puntos con GeoGebra
- Recordar la definición de la gráfica de una ecuación
- Representar gráficamente ecuaciones en GeoGebra
- Visualizar la gráfica de una ecuación en GeoGebra
Conociendo el Software Libre GeoGebra
FuenteGeoGebra es un Software libre dinámico para la enseñanza y aprendizaje de las Matemáticas para educación en todos sus niveles. Combina dinámicamente, geometría, álgebra, análisis y estadística. GeoGebra es en su origen la tesis de Markus Hohenwarter, con el objeto de crear una calculadora de uso libre para trabajar el Álgebra y la Geometría. Fue un proyecto que se inició en el 2001 en un curso de Matemática en la Universidad de Salzburgo (Austria). El cual continúa su desarrollo en la Universidad de Boca Raton, Florida Atlantic University (USA)
Es un programa realizado en Java, por lo que se puede ejecutar en Windows, MacOSX, Linux o Solaris. El programa permite publicar en una página web cualquier construcción que se haya realizado.
Además de ser un software gratuito y la facilidad de aprendizaje, la característica más notable de GeoGebra es la doble percepción de los objetos, pues cada objeto tiene dos representaciones, una en la Vista Gráfica (Geometría) y otra en la Vista Algebraica (Álgebra), es decir combina las representaciones gráficas y símbolos proporcionando ambas al mismo tiempo. Todos los objetos que vayamos incorporando en la zona gráfica le corresponderán una expresión en la ventana algebraica y viceversa.
ACTIVIDAD DE DESARROLLO
PLANO NUMÉRICO
Dos números reales cualesquiera forman un par, y cuando el orden de los números tiene significado se denomina par ordenado. Si x es el primer número real y y es el segundo, este par ordenado es denotado por (x,y). En este sentido, el par ordenado (x,y) es diferente del par ordenado (y,x).
El conjunto de todos los pares ordenados de números reales se llama plano numérico, denotado por R^2, y cada par ordenado (x,y) es un punto en el plano numérico. Para denotar dichos puntos, a cada par ordenado se le asigna una letra mayúscula, de este modo el punto (x,y) se le asocia por ejemplo la letra P y se escribe P=(x,y).
En el par ordenado (x,y), el primer elemento, x, recibe el nombre de abscisa (o bien, coordenada x) de P y al segundo número, y, se le denomina ordenada (o coordenada y) de P.
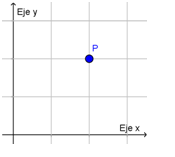
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
(html comment removed: [if !supportLists])1. (html comment removed: [endif])Plano numérico en la interfaz de GeoGebra
Por omisión, la Vista algebraica se abre junto a la Vista Gráfica. La Barra de entrada aparece al pie de la ventana de GeoGebra (versión de Escritorio) o como una Línea de entrada integrada a la Vista algebraica (versiones Web y tabletas). La barra de herramientas gráficas se muestra en el margen superior de la ventana, con los botones Deshace / Rehace en la esquina superior derecha.
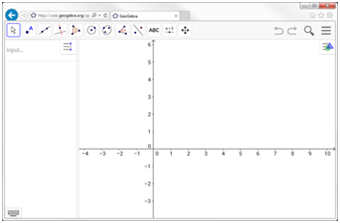
Fuente:GeoGebra Web y Tabletas. Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
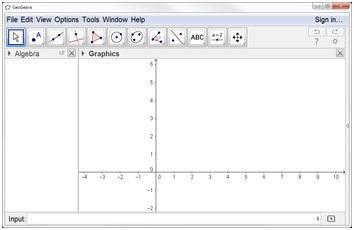
Fuente:GeoGebra escritorio. Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
Antes de iniciar las prácticas te recomiendo leer las siguientes fuentes
- Conociendo el software libre GeoGebra 6.(html comment removed: [if !supportLists])2. (html comment removed: [endif])Puntos con GeoGebra
Los puntos pueden ingresarse directamente en la Barra de Entrada en coordenadas cartesianas (el separador es la coma). Los puntos también pueden crearse con la herramienta Punto además de otros comandos. Los puntos se rotulan con letras mayúsculas, si por error se coloca una letra minúscula GeoGebra lo asumirá como un vector.
Ejemplo: Para ingresar punto el punto P de coordenadas (5,3), en la Barra de Entrada, se anota P=(5,3) y se da Enter esto crea el punto en coordenadas cartesianas, y lo muestra tanto en la vista algebraica como en la vista gráfica.
El menú contextual de un punto (o de un vector) del plano se puede alternar entre la representación Coordenadas cartesianas - Coordenadas polares. Las lecturas de las coordenadas de un punto A (por ejemplo) del plano se conforma por: x(A) e y(A)
En GeoGebra también se puede obtener la distancia entre dos puntos de forma automática, esta se puede obtener de las dos formas siguientes
- Mediante la herramienta Distancia o Longitud (esta herramienta se encuentra en la caja que, por omisión, encabeza la herramienta correspondiente a ), esta mide la distancia entre: dos puntos, dos rectas o un punto y una recta, y la expone como texto dinámico en la vista gráfica. Para usar esta herramienta simplemente se selecciona con el puntero los objetos de los cuales se desea saber su distancia, en la vista algebraica aparecerá la longitud calculada como objeto número asignada a una letra minúscula.
- Mediante la Barra de Entrada, escribiendo el comando Distancia[,] o Distancia[,], en cualquiera de los dos casos para determinar la distancia entre dos puntos A y B (por ejemplo) se escribe Distancia[A,B] y en la vista algebraica aparecerá representado como objeto número como distanciaAB.
Punto medio de dos puntos
Para obtener el punto medio entre dos puntos en GeoGebra, se puede usar uno de las siguientes formas:
- Mediante la herramienta Medio o Centro (esta herramienta se encuentra en la caja que, por omisión, encabeza la herramienta correspondiente a ), un clic sobre:
- un punto y otro punto o un segmento, permite obtener su punto medio.
- una circunferencia, semicircunferencia o sección cónica –como la hipérbola o la elipse–, permite obtener su centro.
- Mediante la Barra de Entrada, escribiendo el comando PuntoMedio[,], el cual crea y registra gráficamente el punto medio entre los puntos indicados. Así, por ejemplo, para determinar el punto medio entre los puntos A y B, se escribe PuntoMedio[A,B].
Práctica 1. Puntos
- Abrir un nuevo archivo de GeoGebra.
- Elige mostrar cuadrícula en la Vista Gráfica.
- Introduce en la Barra de Entrada los puntos A=(3,5), B=(-3,4.2) y P=(-1.5,2).
- Elige la herramienta Punto y crea los siguientes puntos C=(2,-3) y D=(-2,-1).
- Determina el punto medio entre A y P.
- Determina el punto medio B y P.
- Calcula la distancia entre los puntos C y P.
- Calcula la distancia entre los puntos D y P.
- Oculta el texto DP=3.04 haciendo clic en la Vista algebraica sobre el círculo azul al lado del objeto que ocultaras, al hacerlo el círculo aparecerá en blanco.
- Cambiar el color del punto P
<objeto (punto,="" recta,="" cónica...="" )="">
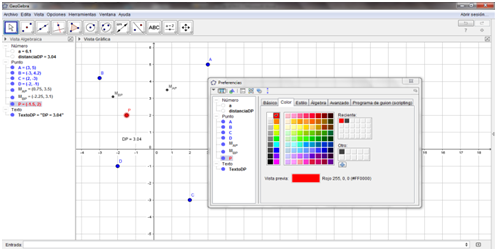 <objeto (punto,="" recta,="" cónica...="" )="">
<objeto (punto,="" recta,="" cónica...="" )="">Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
Práctica 2. Segmentos
- Abrir un nuevo archivo de GeoGebra.
- Elige mostrar cuadrícula en la Vista Gráfica.
- Trazar el segmento que pasa por dos puntos A y B dados. Grafica los puntos (5,3) y (3,-4.2). En la Barra de Entrada escribe seg y elige la opción Segmento[<punto(extremo)>,<punto (extremo)="">], introduce los puntos A y B.
- Trazar el segmento BC. En la barra de herramientas ubica la caja , elige la herramienta Segmento, haz clic sobre el punto B y en el punto C=(0,-1).
- Trazar un segmento de longitud dada En la barra de herramientas ubica la caja , elige la herramienta Segmento de longitud dada, hacer clic sobre un punto para fijarlo como uno de los extremos, en este caso tomar A. Al anotar la longitud deseada en la ventana que se despliega a continuación, se crea y gráfica el segmento, colocar 3.
- Ocultar las etiquetas de los segmentos creados. Hacer clic derecho sobre cada segmento ya sea en la vista gráfica o en la vista algebraica, y en el menú contextual seleccionar la opción Etiqueta Visible.
- Cambiar el color de los segmentos a Azul y en la pestaña Estilo del cuadro Preferencias colocar el Grosor del trazo en 5.
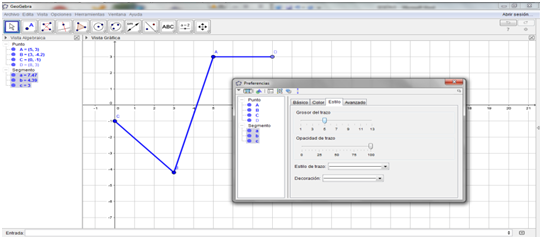 <objeto (punto,="" recta,="" cónica...="" )="">
<objeto (punto,="" recta,="" cónica...="" )=""><objeto (punto,="" recta,="" cónica...="" )="">
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
- Con el ratón selecciona las letras correspondientes a los puntos y arrástralas a un lugar donde sean visibles.
- Determina el punto medio de AB, con la herramienta Medio o Centro, haz clic sobre dicho segmento.
- Pulsa la combinación de teclas Ctrl + A (esto selecciona todos los objetos) y luego presiona Supr (borra los objetos). Cierra la ventana sin guardar.
GRÁFICAS DE ECUACIONES
Una ecuación algebraica con dos variables x y y es un enunciado en el que se establece la igualdad de dos expresiones algebraicas, las cuales contienen a las variables x y y. Cuando x y y se sustituyen por números específicos, digamos a y b, el enunciado resultante puede ser verdadero o falso. Si es verdadero, se dice que el par ordenado (a,b) es una solución de la ecuación.
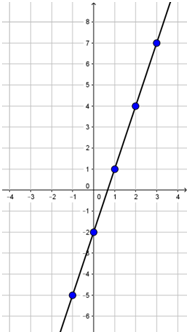
Por ejemplo, algunas de las soluciones de la ecuación y=3x-2 se muestran en la siguiente tabla en conjunto con los pares ordenados que estos forman y su respectiva ubicación en el plano numérico.
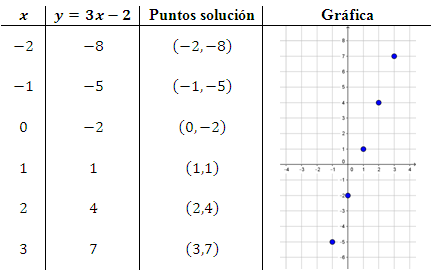
Fuente: Editado en PowertPoint, elaborada por Marilex Porteles y Jesse Rivero
Definición. Gráfica de una ecuación
La gráfica de una ecuación en R^2 es el conjunto de todos los puntos en R^2, cuyas coordenadas son soluciones de la ecuación.
Debido a que la Ecuación anterior tiene un número ilimitado de soluciones, su gráfica consta de un número ilimitado de puntos. En este caso si además de los seis puntos dados en la tabla se colocaran todos los puntos solución, los resultados aparecen ubicados en una recta. La recta es por tanto, la gráfica de la ecuación. Las coordenadas de cualquier punto sobre la recta (x,y) satisfacen la ecuación, y las coordenadas de cualquier punto que no esté ubicado sobre la recta no satisfacen la ecuación.
Nota: Usualmente para indicar que la gráfica continúa aún fuera del recuadro elegido muchos programas colocan flechas en sus extremos, por omisión GeoGebra no coloca estas flechas, aun así se sobreentiende que la gráfica es ilimitada a menos que se indique lo contrario.
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
(html comment removed: [if !supportLists])1. (html comment removed: [endif])Gráficas de ecuaciones con GeoGebra
- Graficar la ecuación y=3x-2
- Abrir un nuevo archivo de GeoGebra
- Ingresar en la barra de entrada la ecuación y=3x-2. En la Vista gráfica aparece la gráfica de la ecuación y en la Vista algebraica aparece la ecuación correspondiente.
La ecuación introducida se puede cambiar para que se exprese de otras formas accediendo al menú contextual de la ecuación, allí aparecen la opción Ecuación ax+by=c y Forma paramétrica.
Al igual que con los puntos y segmentos, a las gráficas de las ecuaciones también se les pueden cambiar sus propiedades, tales como: color, grosor nombre, estilo, etc.
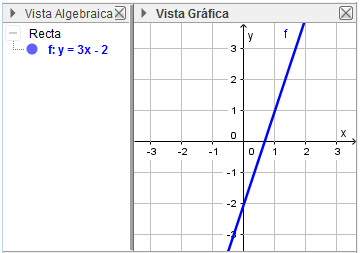
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
- Abrir un nuevo archivo de GeoGebra.
- Ingresar en la barra de entrada la ecuación escribiendo y=x^2-3.
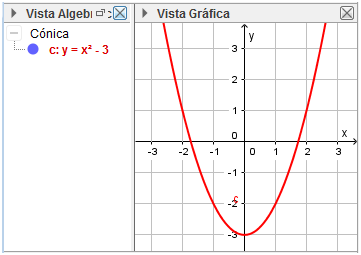
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
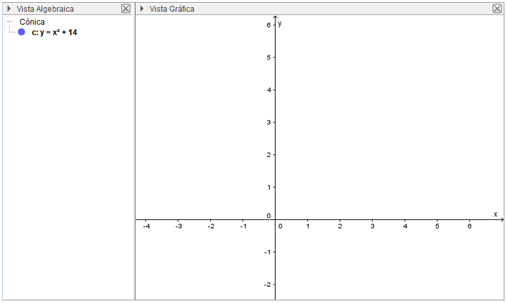
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
Como se puede apreciar en primera instancia aunque la ecuación introducida aparece en la Vista algebraica, en la Vista gráfica no se observa la gráfica de dicha ecuación. Para los pocos experimentados en muchos casos ni siquiera sabrán hacia donde se encuentra la gráfica, tal vez pensarán que cometieron algún error al introducir la ecuación y por tal motivo no aparece o sencillamente asumirán que la gráfica no existe.
En este caso el procedimiento a seguir por parte del usuario es:
- Primero debe hacer clic sobre la vista gráfica para deseleccionar la ecuación.
- Segundo hacer clic derecho sobre la vista gráfica y elegir en el menú contextual la opción Mostrar todos los objetos, esto le llevará hasta la gráfica si esta existe.
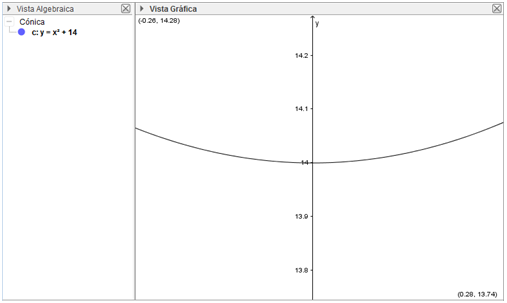
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
- Es posible que aún no se aprecie bien la gráfica, sin embargo, ya se localizó la misma, por lo que el paso a seguir es, mediante el movimiento de la rueda del ratón (zoom) manipular hasta colocar la gráfica en el lugar adecuado, para esto el usuario también puede manipular la proporción de la escala de los ejes.
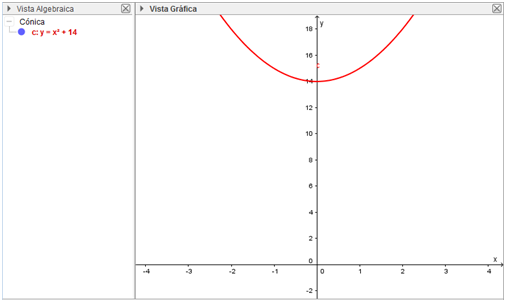
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
- Grafique la ecuación y=√(x+25) y elija la escala y vista adecuada para la gráfica.
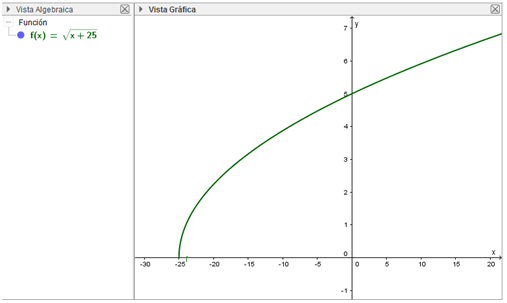
Fuente: Exportada del Geogebra como vista gráfica a imagen. Elaborada por Marilex Porteles y Jesse Rivero
ACTIVIDAD DE CIERRE
Gráfica de varias ecuaciones en una misma ventana de GeoGebra.
GeoGebra permite ingresar múltiples ecuaciones en una misma ventana sin ningún inconveniente, esto permite ver las relaciones entre ecuaciones e incluso propiedades comunes.
Graficar las ecuaciones siguientes en una misma ventana de GeoGebra:
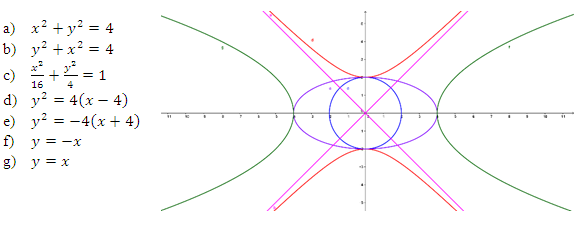
Fuente: Exportada del Geogebra como vista gráfica a imagen y editada en PowerPoint. Elaborada por Marilex Porteles y Jesse Rivero

- González, M. (sf). Geogebra. Disponible:https://sites.google.com/site/geogebra1112/caracteristicas-de-geogebra
- Hohenwarter, M. (2014). Multiple representations and GeoGebra-based learning environments. Unión. Revista Iberoamericana de Educación Matemática, 39, 11-18
- Manual del GeoGebra. Preparativos de la Vista Gráfica. Disponible: https://wiki.geogebra.org/es/Preparativos_de_la_Vista_Gr%C3%A1fica
ATENCIÓN
NOTA
- El POST fue subido utilizando la aap oficial de https://www.steemstem.io


Genial el contenido @xeliram. Te gustaría compartir tus conocimientos en el área de matemáticas con toda la comunidad en discord por medio de un conversatorio?
Hola @carlosserp-2000, gracias por la invitación, pero mi computadora se daño y desde que me instalaron el sistema operativo no he podido conectarme con discord pues me sale:
correo electrónico: se ha detectado un inicio de sesión
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider setting @steemstem as a beneficiary to your post to get a stronger support.
Thanks for having used the steemstem.io app. You got a stronger support!