Inequality: Always, sometimes or never?

tradersharpe (57)in #steemstem • 7 years ago (edited)

alwaysSometimesNever -- 00.png

"Always, sometimes or never?"

"Is it always true, sometimes true or never true?"

These are questions that we should ask for everything in life, including mathematics. However, many students are accustomed to a fixed way of doing things, a fixed set of procedures to follow, a fixed type of solutions to problems. They will coast along until they encounter the following type of problem.

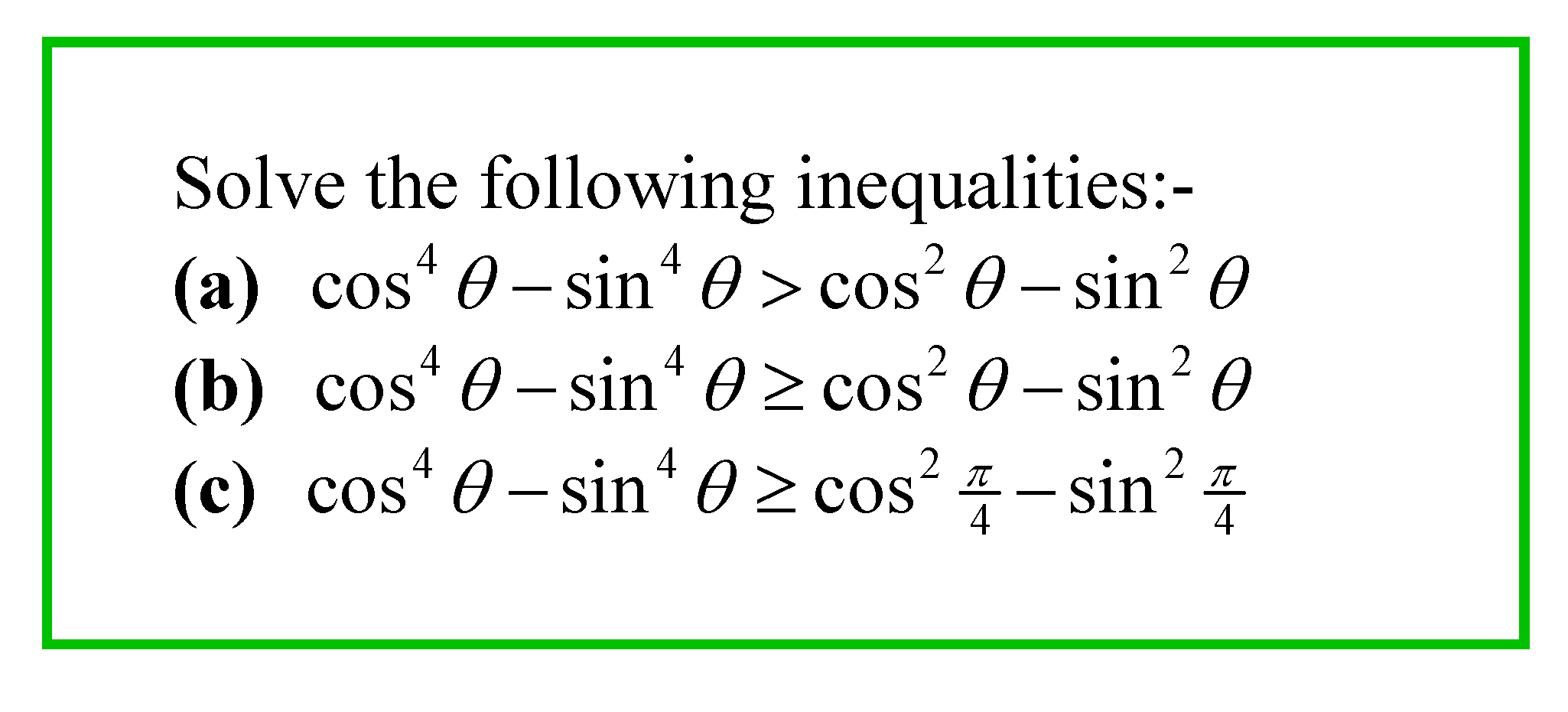
alwaysSometimesNever -- 01.png

"What?!? I am used to seeing equations like 3 x + 1 = 7 which have one answer, and equations like x² = 9 which have 2 answers and inequalities like 2 x - 1 > 5 which has a range of answers, but not those above!?!"

Certainly so. This question is a little bit more challenging. But do not panic. Try to look for patterns. Observe that ${\cos^{4}\theta-\sin^{4}\theta=(\cos^{2}\theta)^2-(\sin^{2}\theta})^2$ can be split up as ${(\cos^{2}\theta+\sin^{2}\theta)(\cos^{2}\theta-\sin^{2}\theta)}$ using the difference of squares ${a^2-b^2=(a+b)(a-b)}$ formula, with ${a=\cos^{2}\theta}$ and ${b=\sin^{2}\theta}$ .

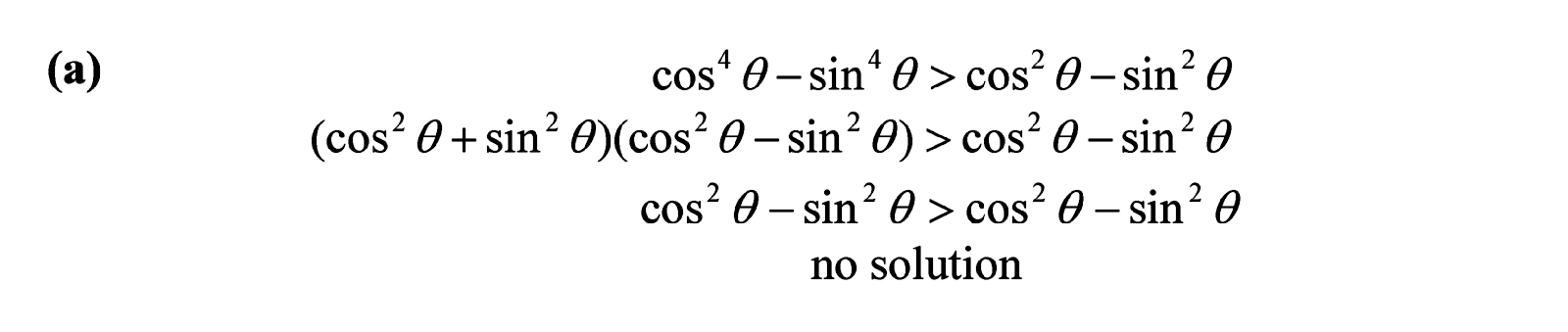
alwaysSometimesNever -- 02.png

Remembering that ${\cos^{2}\theta+\sin^{2}\theta=1}$ which is an identity (so it always true), we end up with a silly statement like ${\cos^{2}\theta-\sin^{2}\theta}>\cos^{2}\theta-\sin^{2}\theta$ which is never true. So there is no solution for part (a).

For part (b) we proceed similarly.

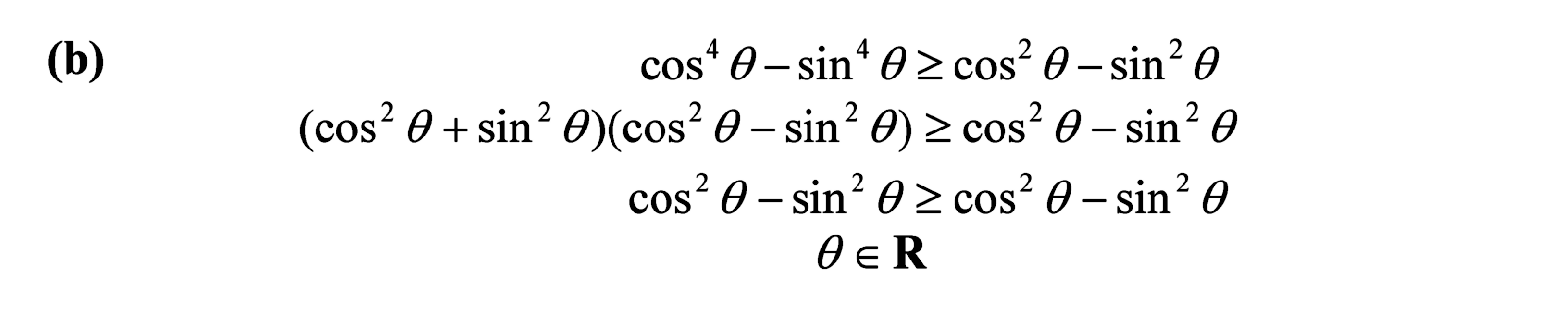
alwaysSometimesNever -- 03.png

We end up with a the statement like ${\cos^{2}\theta-\sin^{2}\theta}\ge\cos^{2}\theta-\sin^{2}\theta$ which is always true. Everything is always greater than or equal to itself. Even though the "greater than" part is not true, the "equal" part is definitely true. So the statement is considered as true, for whatever value of theta you care to substitute in it. That means theta can be any real number. The solution set is the set of all real numbers.

Now for the clincher!

Again we proceed as in parts (a) and (b) but note that both ${\cos(\frac{\pi}{4})}$ and ${\sin(\frac{\pi}{4})}$ are equal to ${\frac{1}{\sqrt{2}}}$ , which makes the Right Hand Side zero. On the Left Hand Side, note that ${\cos^{2}\theta-\sin^{2}\theta}=\cos{2\theta}$ , so the question now becomes when is ${\cos{2\theta}}$ greater or equal to zero.

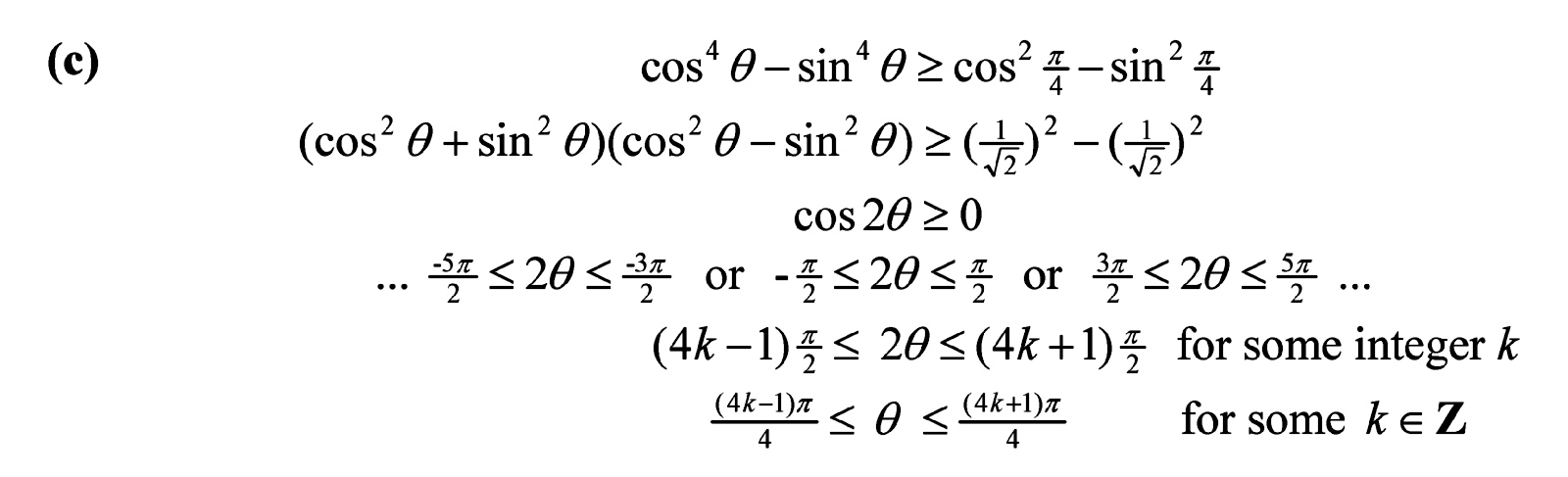
alwaysSometimesNever -- 04.png

You may want to use the ASTC or "All Science Teachers are Crazy" mnemonic to help determine the quadrants where the cosine is positive or negative. For me, I prefer to consider the fact that the cosine is just the x-coordinate on the unit circle, so the cosine is positive on the right two quadrants (quadrants 1 and 4). We know that ${\cos{2\theta}}$ is non-negative from -90 degrees to 90 degrees, or from ${-\frac{\pi}{2}}$ to ${\frac{\pi}{2}}$ radians. But we can go round and round the circle, clockwise and/or anti-clockwise indefinitely to get other solutions. This means we keep on adding or subtracting 360 degrees or ${2\pi}$ radians. It turns out that there is a pattern. ${2\theta}$ must be from ${(4k-1)\frac{\pi}{2}}$ to ${(4k+1)\frac{\pi}{2}}$ , where k is some integer. Dividing the inequality through by 2 gives our final answer.

In conclusion

When solving inequalities or equations, we should consider the possibility that the it may always be true, or never be true, or sometimes true.

I hope you have learned something solving these challenging inequalities.

Image Credits

The first picture was derived from Pixabay, while the rest are all my own work.

Announcements

You might also want to read my recent articles:
Integral of 1/sqrt(e^2x+1) (Trigo Approach)
Simplifying Roots
"Singapore Math": The Ribbons Problem from PSLE 2017

If you find my articles useful or interesting, please upvote and resteem them! Thanks !

Cheers!!!

@tradersharpe
-- promoting sharp minds

#steemiteducation #mathematics #math #science

7 years ago in #steemstem by tradersharpe (57)

Sort:

minnowbooster (73) 7 years ago

Calling @originalworks :)
_{img credz: pixabay.com}
Nice, you got a 7.0% @minnowbooster upgoat, thanks to @tradersharpe
Want a boost? Minnowbooster's got your back!

originalworks (69) 7 years ago

The @OriginalWorks bot has determined this post by @tradersharpe to be original material and upvoted it!

ezgif.com-resize.gif

To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
For more information, Click Here!
Special thanks to @reggaemuffin for being a supporter! Vote him as a witness to help make Steemit a better place!

booster (68) 7 years ago

This post has received a 1.44 % upvote from @booster thanks to: @tradersharpe.

minnowpond (62) 7 years ago

@driva has voted on behalf of @minnowpond.
If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.

            To receive an upvote send 0.25 SBD to @minnowpond with your posts url as the memo
            To receive an reSteem send 0.75 SBD to @minnowpond with your posts url as the memo
            To receive an upvote and a reSteem send 1.00SBD to @minnowpond with your posts url as the memo

newjkc (31) 7 years ago

Your thinking is better. Actually who have energy & wisdom is creative.

$0.00

qurator (76) 7 years ago

Qurator	Your Quality Content Curator
	This post has been upvoted and given the stamp of authenticity by @qurator. To join the quality content creators and receive daily upvotes click here for more info. ^{Qurator is proudly supported by @reggaemuffin, vote for him as a witness here.}

$0.00

reggaemuffin (66) 7 years ago

Dang yeah, that stuff is what many students struggle with. 🐐

$0.00

kfjony (30) 7 years ago

Mathematical terms & condition very tough.

$0.00

jaynie (75) 7 years ago

If only I had you around when I was in school! @tradersharpe ;)

$0.00

minnowpond (62) 7 years ago

@cmtzco has voted on behalf of @minnowpond.
If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.

            To receive an upvote send 0.25 SBD to @minnowpond with your posts url as the memo
            To receive an reSteem send 0.75 SBD to @minnowpond with your posts url as the memo
            To receive an upvote and a reSteem send 1.00SBD to @minnowpond with your posts url as the memo

$0.00

rajuahamed (6) 7 years ago

hi frineds nice post and give vote good

$0.00

light-o-trix (46) 7 years ago

https://steemit.com/steemstem/@light-o-trix/defense-strategy-and-capabilities-development-across-the-globe-is-it-a-threat-for-the-human-race

$0.00

STEEM 0.27

TRX 0.20

JST 0.038

BTC 96668.41

ETH 3695.55

USDT 1.00

SBD 3.86