Infinity and Beyond - Part 3

Image Source
Roadmap
"Infinity and Beyond" is a series of posts about the concept of infinity, its mathematical properties and how misleading our intuition about infinity can be. It will get rather technical but I will try my best to make it as easily digestible as possible. You do not need to have studied Mathematics or a related field to understand this series.
- Part 1 - Introduction
- Part 2 - Why is Infinity plus One not larger than Infinity?
- Part 3 - Can we go bigger?
- Part 4 - Interesting Thought Experiments depending on Infinity
These are the already planned parts. This list may be subject to change.
Can we go Bigger?
In the previous parts of this series of articles we established that adding finitely many elements to an infinite set does not change its size. We looked at a way to prove that two sets are the same size and played around with the natural numbers a little. But can we go bigger?
Yes, there are sets bigger than the set of all natural numbers even though the set of natural numbers is already infinite. We learned that to prove two sets to be the same size we simply need to find a bijection from one set into the other. However to disprove that two sets are the same size we would have to show that no such function exists. That's no easy task as there are at least as many functions as there are natural numbers, i. e. infinitely many. Because humans only have finite lifespans though it is hard to prove that all functions from one set to another are not bijections. In order to prove the inequality of set sizes we need to stay with the size of the natural numbers just a little longer.
While we are at it, let's give the size of the natural numbers a name. We use the natural numbers for counting. I guess the name "countably infinite" will do. (Full disclosure: I did of course not come up with this name. It's the actual mathematical term for it.)
The set of all rational Numbers
Let's take a look at the set of all rational numbers, i. e. the set of all whole fractions of all whole numbers. If you take all whole numbers and one after the other divide them by all natural numbers you get the set of all rational numbers.

(Remember that zero is not a natural number.)
The set of all rational numbers is the same size as the set of all natural numbers, it is countable. That may be a little harder to believe than just adding one element to a set. And yes, finding a bijection for this is quite a bit harder. If you want, take some time to think of one before reading on.

Image Source
Formulating a mathematical function for this set would be quite hard and cumbersome, so we'll be doing something else. So far we were looking at the general case of just comparing two arbitrary sets. In this case we only want to see if the set is the same size as the natural numbers, i. e. if it is countable.
If we can find a way to count all elements without missing one or leaving one out, we basically have created an surjection from the natural numbers to that set (reaching all elements is the definition of surjective). We just need to make sure to never miss any element.
If you have read the previous part to this series of articles you may now say "Wait... Don't we need a bijection, so something that is both surjective and injective!?". Yes, that is true if we compare arbitrary sets. However, we only want to show that the rational numbers are countable, or in other words, that the rational numbers are at most as large as the natural numbers. Finding a surjection does just that. Finding a bijection shows equality, finding a surjection shows that the target set is at most as large as the original set.
Surjective [...] means that all elements from the output set are reached by means of the function and the input set. Or in other words, there exists no element in the output set that can not be produced by the function and an element from the input set.
Quoted from part 2.
Luckily enough, countable infinity is the smallest infinity (mathematical proof of this can be found here thanks to @mathowl). So finding a surjection from the natural numbers to the target set is sufficient to show countability and even equal size to the set of the natural numbers. Why is it the smallest? Well, take any infinite subset of the natural numbers and you can always find a bijection onto the natural numbers, i. e. they are the same size, ergo there is no infinite set smaller than the natural numbers.
Alright, so it's enough to find a way to count the rational numbers and we don't have to worry about counting elements twice. Remembering the definition of the rational numbers "all numbers a divided by b with all whole numbers a and all natural numbers b" let's first find a way to write them all down. Make a table and write all whole numbers in the header and all natural numbers at the beginning of each row. Now in each inner field of that table we just write the number a/b (a divided by b) where a is the column header and b is the row header.
| 0 | -1 | 1 | -2 | 2 | -3 | 3 | ⋯ | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0/1 | -1/1 | 1/1 | -2/1 | 2/1 | -3/1 | 3/1 | |
| 2 | 0/2 | -1/2 | 1/2 | -2/2 | 2/2 | -3/2 | 3/2 | |
| 3 | 0/3 | -1/3 | 1/3 | -2/3 | 2/3 | -3/3 | 3/3 | |
| 4 | 0/4 | -1/4 | 1/4 | -2/4 | 2/4 | -3/4 | 3/4 | |
| 5 | 0/5 | -1/5 | 1/5 | -2/5 | 2/5 | -3/5 | 3/5 | |
| ⋮ | ⋱ |
Looking at this table and the definition of the rational numbers it is easy to see that those are in fact all rational numbers. Now let's see how we could count those. Well, we can't do row by row, because if you follow a row from left to right with the intention of counting the second row after you finished the first one, that wont work. Each row is infinitely long and you would never reach an end of that row, thus never counting any row but the first one. Columns? Same problem here, each column is infinitely long.
Let me grab a pen and some paper to show you. (I'll leave out the internal values to keep my hand from cramping.)
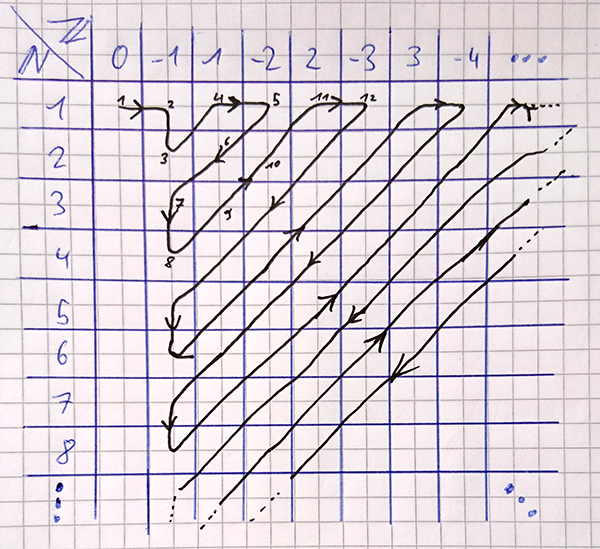
That way we can count all rational numbers. Since the bottom-left to top-right diagonals are all finite, we can easily count one after the other. The first column is mostly neglected because it only contains zeros. While counting numbers twice is okay, there is no need to do it on purpose.
Since we found a way to count the rational numbers without ever leaving any rational number out, we have shown that the rational numbers are countably infinite.
Give me something Bigger!
I have promised you something bigger and I will deliver. It was just important to give you an idea of how writing something in a different way can lead you to an easy way of solving something. With that out of the way let's finally look at something bigger.
Drum roll please.
The real numbers! The set of the real numbers contains all rational numbers and all irrational numbers. Irrational numbers are all numbers that cannot be described as a ratio of whole numbers. This results in infinitely long, non-repeating decimals. Like the number pi. Here are the first 76 digits of pi:
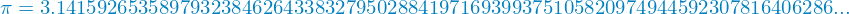
However those are not all of them. Pi goes on and on and on, never repeating and never ending. If you want to see a mile long, one million digits of pi printed out you can head over to Numberphile on Youtube. If you like my content, chances are you'll like theirs.
Even with rational numbers you can always find another rational number in between two arbitrarily close rational numbers. But in between each and every two rational numbers, no matter how close they are, there are also infinitely many irrational numbers in between those. You can already see that we have several layers of infinity in the set of all real numbers. The real numbers are so tightly packed, i. e. there are so many numbers between any two arbitrarily close numbers, that we cannot count them anymore. It is impossible to find a way to count them, without missing one. Even if you have an infinite amount of time, the real numbers are uncountable. How are we going to prove this though.
The diagonalization Argument
Cantor's diagonalization argument is one more of those cases where just writing things differently can lead you to an easy solution.1 To make our lives even easier we will only look at a tiny subset (in comparison to the whole) of the real numbers. We only consider the real numbers in the interval from 0 (inclusive) and 1 (exclusive), that only consist of the digits 1 and 0. For example 0.011011101001, or 0.100001 and so on. If we can show that this tiny subset is uncountable then the whole of the real numbers are definitely uncountable.
For writing them down we are going to ignore the "0." as that just comes before all numbers we are looking at (the number 0.0010101 is represented by 0010101). The order in which we are writing them down (i. e. counting them) does not matter, but we need to remember that they are infinitely long. With those things in mind let's start writing down numbers. One in each line and start each line with the index of the number, i. e. order them in the way we are trying to count them.
| index | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | ⋯ |
| 2 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | ⋯ |
| 3 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | ⋯ |
| 4 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | ⋯ |
| 5 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | ⋯ |
| 6 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ⋯ |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ⋯ |
| ⋮ | ⋱ |
Those are numbers all right. But are those really all the real numbers? Or rather, can we write down all real numbers in the small subset we chose in this way? Well, let's just take a look at the diagonal of this table. (Marked in bold for your convenience.)

(Remember, this represents the number 0.0101101... infinitely extended with some digits.)
Okay, that's also a number of our set. Just for fun, let's invert this number by making any 0 digit a 1 and vice versa.

Oh oh. This is problematic. What have we just done there? We have taken the diagonal. The diagonal is certainly a number in our set. We have inverted the diagonal (substituting 0 for 1 and vice versa). That number too is part of the set we are considering.
Now since all lines extend infinitely and all columns extend infinitely this means that each and every number we wrote down contributes exactly one digit to the diagonal. This means though that each and every number we wrote down differs from the inverted diagonal in at least one digit. So no matter what numbers we write down and no matter for how long we do this, we will never be able to write down the inverted diagonal in our list. This means, we are missing at least one number of the set we want to count.
As a result the set of all real numbers between 0 and 1 consisting only of the digits 0 and 1 are uncountable. And thus the real numbers cannot be countable. The set of real numbers is truly larger than the set of the natural numbers, even though both are infinite.
Image Source
Okay, you may need to read the paragraph above a few times. Try to imagine what would happen if you were to try and add the inverted diagonal at some point. If you added it, it too would contribute to one digit of the diagonal. This would now change the diagonal and we would have a different inverted diagonal, that we would now have to add too. It is a paradox, that cannot be resolved. This paradox happens because the real numbers are uncountable.
If it is still not clear to you, please do shout at me in the comments for explaining it badly. I will try my best to make each and everyone reading this understand this.
How big can we go then?
How big would you like? There are infinitely many different degrees of infinity or "cardinalities". The German mathematician Georg Ferdinand Ludwig Philipp Cantor (1845 - 1918), yes the one with the diagonalization argument we used earlier, has conducted extensive research in the realm of infinity. He found out that the power set of any infinite set has a higher cardinality than the original set.2
A power set is the set of all possible subsets. Here is one example of a power set.
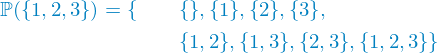
As you can see, things get out of Hand pretty quickly. The power set of a set with merely three elements already has eight elements. The power set of a set of size 10 already has 1024 elements. In general a set of size n has a power set of size  .3
.3
Just by using the power set operation you can create larger and larger infinite sets, each bigger than the one before.
Aleph
Cantor worked on a notation for infinite cardinalities. He used the hebrew letter Aleph for this.
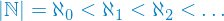
Aleph-naught (also called Aleph-zero or Aleph-null) is the size of the natural numbers. Each following Aleph is bigger than the one before. You may now ask yourself if Aleph-one is equal to the amount of real numbers. The answer to this isn't so simple. It has only been proven with certain axioms applied, basically with additional preconditions that we cannot prove, but just assume are true.4 We are not going to explore this idea here however.
This Aleph notation gives us a convenient way of going crazy to find bigger and bigger cardinalities. You could for example use Aleph-aleph-0 so the aleph-0-th infinite cardinality. Yes, this means there are countably infinite cardinalities smaller than this one. Our feeble minds can barely understand countable infinity, but this is truly unbelievable.
Conclusion
We have proven that the rational numbers are as numerous as the natural numbers, but that the natural numbers are less numerous than the real numbers. I have shown you a notation for infinities and we realized that there even is an unbounded amount of cardinalities. You can always, always, always find a bigger one.
This concludes the purely theoretical part of this series. Next time we will go over a short list of some interesting theoretical problems involving infinity. If you have a problem/conundrum/thought experiment about or involving infinity that you really liked do let me know in the comments and I may include it in the next part.
If you are interested in the idea behind Alephs and a slightly different approach, to infinity I can highly recommend the video How To Count Past Infinity by VSauce.
Thank you very much for reading and please let me know if anything was unclear or if there are any questions left.
- Cantor's diagonalization argument - https://en.wikipedia.org/wiki/Cantor%27s_diagonal_argument
- Georg Cantor - https://en.wikipedia.org/wiki/Georg_Cantor
- Proof for size of power sets - https://www.math.utah.edu/~pa/math/sets/powerproof.html
- Aleph numbers - https://en.wikipedia.org/wiki/Aleph_number
Big thanks to @mathowl for the mathematical proof of countably infinite being the smallest infinity.
Equations created with latex2png.
Deutsche Version hier.
I don't understand this
What do you mean by infinite subset? It seems like you are taking a subset with the same cardinality....
I see your point. I think I'll have to do some more research on this. It is rather late here though, so I'll get back to you tomorrow.
The easiest way to prove it is by using axiom of choice. It is a bit harder to prove it without using axiom of choice.
Well a place where the axiom of choice does not hold is pretty scary. Hope you don't have nightmares ;)
Ok, so I have come to the point where I don't see how you can prove it without assuming the axiom of choice (AC). I think I will add that to the text with a link to the axiom. And I couldn't find one.
If you can find or construct a proof that does not require AC I would very much appreciate it, as I would like to avoid mentioning AC in fear of it confusing people. The target audience of this post are non-mathematicians after all.
I don't think the proof without axiom of choice is suitable for non-mathematicians. I will put it in a post since I cannot find the proof in any literature. You can try to simplify it if you think it is worth your time.
Thank you, I'm looking forward to your post! 😃
Here is the post https://steemit.com/mathematics/@mathowl/countable-infinity-is-the-smallest-cardinal-infinity-even-without-assuming-the-axiom-of-choice-warning-technicalities-await