Infinity and Beyond - Part 2

Image Source
Roadmap
"Infinity and Beyond" is a series of posts about the concept of infinity, its mathematical properties and how misleading our intuition about infinity can be. It will get rather technical but I will try my best to make it as easily digestible as possible. You do not need to have studied Mathematics or a related field to understand this series.
- Part 1 - Introduction
- Part 2 - Why is Infinity plus One not larger than Infinity?
- Part 3 - Can we go bigger?
- Part 4 - Interesting Thought Experiments depending on Infinity
These are the already planned parts. This list may be subject to change.
Why is Infinity plus One not larger than Infinity?
In the previous part of this article we discovered an infinite set with which we are all familiar, the set of natural numbers 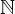 . Let us now take a deeper dive in what infinity means and what happens when we add elements to an infinite set.
. Let us now take a deeper dive in what infinity means and what happens when we add elements to an infinite set.
Adding to an Infinite Set
Now that we have an infinite set to play around with, lets see what happens to its size if we add something to it. Say we want the number 0 to be part of it as well (as stated in part 1 we defined zero to not be a natural number). Also lets call the new set 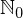 just so we don't confuse them. The mathematical way of adding the element 0 to a set would look like this.
just so we don't confuse them. The mathematical way of adding the element 0 to a set would look like this.
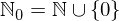
We take the natural numbers and join them with the set that only contains the number 0 and we end up with the set we wanted. At this point try to make a prediction of how the sizes of  and
and 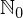 compare.
compare.

Image Source
Our intuition may claim that 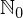 surely must be larger than
surely must be larger than 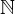 , we added an element after all. Remember though that we are here to prove that infinity plus one is equal to infinity. So if you believed your intuition you have been lead astray. The sets
, we added an element after all. Remember though that we are here to prove that infinity plus one is equal to infinity. So if you believed your intuition you have been lead astray. The sets 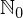 and
and 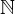 are the same size.
are the same size.
If you don't believe me or don't see how this can work keep reading. I will guide you step by step to understand this.
Puzzle Pieces for the Proof
Warning mathematical formulae incoming. Brace yourselves but do not be worried. I will go though everything step by step and make everything as comprehensive as possible.
The great thing about mathematics is that you don't just have to (or even should) believe me. You don't even have to (or should) believe a highly decorated maths professor. Only ever trust in hard proof. So let me prove it to you.
Intermission
At this point a rather famous paradox/thought experiment should be mentioned: "Hilbert's Grand Hotel". This thought experiment used to confuse me more than it helped though, because it tries to give a pseudo real-world example of an infinite hotel, something which obviously can't exist. I am not good in wrapping my head around pseudo real-world examples trying to explain something purely theoretical. For this reason I will not go into Hilbert's Hotel but give a purely theoretical proof for our little problem. If you, esteemed reader, are interested in Hilbert's Hotel, or if those pseudo real-world examples help you, here is a good article about Hilbert's Grand Hotel.
So let's take a moment to think about how we could do this. We have two sets. Each set has elements and we need some way to compare these sets. There is one thing in mathematics that you may not have associated with sets if you are not "into" maths: Functions. Mathematically speaking function are just mappings from one set into another. Take for example this basic function:
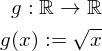
The function g is defined to map from the real numbers into the real numbers in such a way, that the number x is mapped to the square root of x. Most everyday functions are defined over the real numbers but those too are just a set and you are free to chose different ones for your function.
One Function to rule them All
Since we want to compare the two sets from earlier, namely 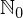 and
and 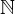 . Lets find a function that maps from
. Lets find a function that maps from  to
to  .
.
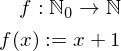
With our rather limited sets we now need to check that this is actually a valid function by confirming that we stay within the sets we defined. Meaning if you apply the function to any element of 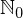 the result needs to be an element of
the result needs to be an element of 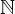 . In order to do this we first check the edge case, i. e. the smallest element of
. In order to do this we first check the edge case, i. e. the smallest element of 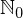 which is
which is 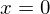 .
.
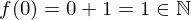
(Remember that
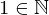 means that 1 is in fact an element of the set
means that 1 is in fact an element of the set  .)
.)Yup, this is okay. What else do we need to check, well for any 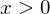 we are fine because we only add to it, so we will never end up below 1, which would be outside of the natural numbers. Since we only add an integer to other integers the result will only ever be an integer, so we don't accidentally have rational or even irrational numbers. (This was a very much informal proof for the sake of readability.)
we are fine because we only add to it, so we will never end up below 1, which would be outside of the natural numbers. Since we only add an integer to other integers the result will only ever be an integer, so we don't accidentally have rational or even irrational numbers. (This was a very much informal proof for the sake of readability.)
Okay, we have a function that maps from one of our sets into the other. Were we not here though to prove that they are the same size? How does a function help us here? As will become apparent in a moment the choice of function was deliberate. This function has some very useful properties that will help us prove what we came here to prove.
Bijections
Our function 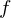 happens to be a bijection. Bijective means it is both injective and surjective (Duh...).1 I know that explanation doesn't help, so let me tell you what injective and surjective means:
happens to be a bijection. Bijective means it is both injective and surjective (Duh...).1 I know that explanation doesn't help, so let me tell you what injective and surjective means:
Injective means that any two distinct elements from the input set (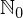 ) are never mapped to the same element in the output set (
) are never mapped to the same element in the output set (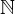 ). Or in other words, if you look at any result of our function you know there was one and only one input that could have created that output.2
). Or in other words, if you look at any result of our function you know there was one and only one input that could have created that output.2
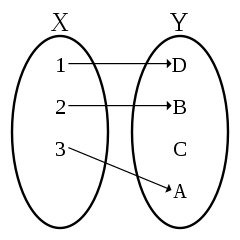
Image Source
Surjective on the other hand means that all elements from the output set are reached by means of the function and the input set. Or in other words, there exists no element in the output set that can not be produced by the function and an element from the input set.3
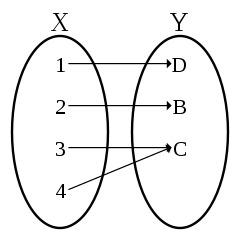
Image Source
Again, I will not formally prove that our function is bijective for the sake of readability, but prove it informally: Since the function 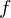 adds 1 to its input, no two input elements will ever be mapped to the same output because adding one will only produce the same output for the same input, i. e. it is injective. Since the input set
adds 1 to its input, no two input elements will ever be mapped to the same output because adding one will only produce the same output for the same input, i. e. it is injective. Since the input set 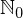 is infinite and thus will never run out, we can create all elements from the output set
is infinite and thus will never run out, we can create all elements from the output set 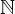 using
using 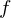 and the input set, i. e. it is surjective.
and the input set, i. e. it is surjective.
Anyone, who wants to see a formal proof of our function being a bijection can look it up here.
Fitting the Pieces to Prove our Conjecture
We have established the following.
- Our set
 is the set of natural numbers in addition to the number 0.
is the set of natural numbers in addition to the number 0. - We have created a function
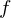 that can map from
that can map from  into the natural numbers.
into the natural numbers. - That function is bijective.
Lets see again what bijective means. Bijective means, that the function maps each distinct element of 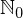 to a distinct element of
to a distinct element of  and all elements from
and all elements from  have been mapped, are reachable so to speak.
have been mapped, are reachable so to speak.
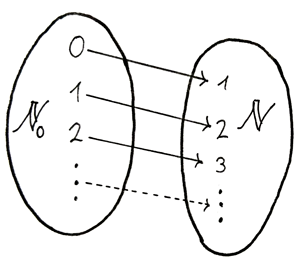
Image made by me
Since a bijective function from 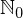 to
to 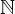 exists, i. e. we never map an output twice and all elements from
exists, i. e. we never map an output twice and all elements from 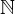 can be created using elements from
can be created using elements from 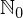 , both sets must be of the same size!
, both sets must be of the same size!
If the input set was bigger than the output set we would have to map more than one input element to the same output element (we would run out of outputs), which would mean there can be no injective function.
If the output set was bigger than the input set we would have output elements that are not mapped at all (we would run out of inputs), which would mean there can be no surjective function.
However we did find a bijective function from 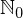 to
to 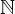 , so both sets must have the same amount of elements. Even though we added an element to one of them.
, so both sets must have the same amount of elements. Even though we added an element to one of them.
In general we can say that any two sets are the same size iff. (read "if and only if") there exists a bijective mapping/function from one set into the other.4 Casting this into mathematical terms may look like this.
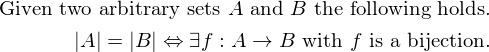
(
 means "there exists a...")
means "there exists a...")Intermission
The abbreviation "iff." is often used in mathematics and means "if and only if". This is a convention to avoid the imprecisions of natural language. To say "A is true iff. B is true" means if A is true, B has to be true, but also if A is not true B cannot be true, and vice versa. If we used the simple "if" on the other hand, we would have an implication instead of an equivalence. I. e. a statement that is not reversible. To say "A is true if B is true" means that A is true if B is true, but if we know that B is true we do not know whether or not A is true as well.

Image Source
Conclusion
We have just proven that adding one element to an infinite set does not change its size.
In fact adding any amount of finite elements to an infinite set does not change its size. Analogously to our function from before we could just increase how much we add to the input number.
Amazing, isn't it?
But does that mean that there is only one kind of infinity and all infinities are the same size? No, not at all! If you are curious to see something bigger than the amount of natural numbers, stay tuned for the next part.
In the meantime I hope this was understandable for everyone. If you have any questions, want to see more formal proof or want to give me some feedback, the comment section is right there for you.
More Fun?
There are of course more sets that are seemingly bigger than one another but are really the same size. I'll give you some examples and if you want, you can try to figure out what function would give a bijective mapping in order to prove that they are the same size. In order of increasing difficulty:
- The set of all even numbers
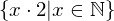 (read as "the set of x times 2 with all x from the natural numbers") and the set of all natural numbers
(read as "the set of x times 2 with all x from the natural numbers") and the set of all natural numbers 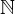 .
. - The set of all whole numbers
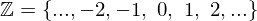 and the set of all natural numbers
and the set of all natural numbers  . Hint: The function needs to be a bijection, but it does not need to be monotonous i. e. the values may jump around as much as you like.
. Hint: The function needs to be a bijection, but it does not need to be monotonous i. e. the values may jump around as much as you like. - The set of the natural numbers
 and the set of the rational numbers
and the set of the rational numbers 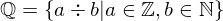 . Note though that is quite a tough challenge and will be a topic on the next part of this series.
. Note though that is quite a tough challenge and will be a topic on the next part of this series.
- Bijection - https://en.wikipedia.org/wiki/Bijection
- Injection - https://en.wikipedia.org/wiki/Injective_function
- Surjection - https://en.wikipedia.org/wiki/Surjective_function
- Only source I could find were non-public lecture notes from my Complexity Theory Professor. Please leave a comment if you know about any public sources on this.
- Hilbert's Grand Hotel - https://plus.maths.org/content/hilberts-hotel
Note: Most of the proofs were informal for the sake of digestibility. However, if you want to see formal proofs for anything in this article let me know in the comments and I will provide them.
Equations created with latex2png.
This is a test comment, notify @kryzsec on discord if there are any errors please.
Being A SteemStem Member
Part 3 is out!
Also
...where f is a bijection or ..with f a bijection
Assuming you mean the odd/sloppy phrasing. Yes, I should probably rephrase that.
Perhaps you could write a formal proof of the bijection, on a side note, just so one can see how it would look like. I think we must not fear losing readership by being a bit technical, especially since you did a great job giving an informal explanation.
I think I'll make the bijection proof another post and then link to it from this article. I think that way it is least intrusive to anyone who is not interested, but there for the people who want to see it.
No promises, but I'll try to get it done by tomorrow.
thanks!
Hey there, the formal proof is now up. You can find it here.
This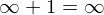 in terms of notation has no meaning. You cannot just add to infinity. You should use the earlier defined operator f to make this statement correct.
in terms of notation has no meaning. You cannot just add to infinity. You should use the earlier defined operator f to make this statement correct.
I was arguing with myself whether or not to add that. You are right. I think the argument still works when removing it, so I will just remove it.
Thank you for your feedback :)
Deutsche Version hier.
Although I like the idea of this post I think you can explain it simpler since you are only considering countable infinity. Of course if you add a single element to something which is countable it will still remain countable.
Since the post is aimed at the layman and tries to lay the foundations of the mathematical idea of infinity I felt a thorough explanation/proof was needed. Also I would argue that it is not so obvious. When I first learned about this it took a bit of getting used to.
And psssst... your spoiling things. Just kidding. The next part of this series will be about uncountable sets and diagonalization. After all I haven't even introduced the name "countable infinity" yet, because so far we have only looked at one type of infinity.
I guess it is a matter of taste. But I do think that countability is a natural concept since it essentially corresponds to counting. Countability in a finite setting then gives rise to countability in an infinite setting.
@blackiris wrote a nice post about the basic concept of infinity. If you have free time check it out :) https://steemit.com/mathematics/@blackiris/lamentations-in-a-sanatorium
Well, the title of the post sure does sound promising! :D I will make sure to give it a read.
Thanks for your input! :)
Congratulations @targodan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP