Introduction to TRUSS- definition and some basic assumptions

This post is basically meant to be the introduction of TRUSS . Which is a very important topic regarding to structural analysis and design. The definition of trusses and some basic assumptions and methods to solve mathematical problems related to TRUSS MEMBERS or TRUSS STRUCTURES.

Definition of TRUSS

Truss is a system of uniform bars or members ( of circular sections, angle sections etc. ) joined together at their ends by riveting or welding and constructed to support loads.

- The members of a truss are straight members and the loads are applied only at the joints.

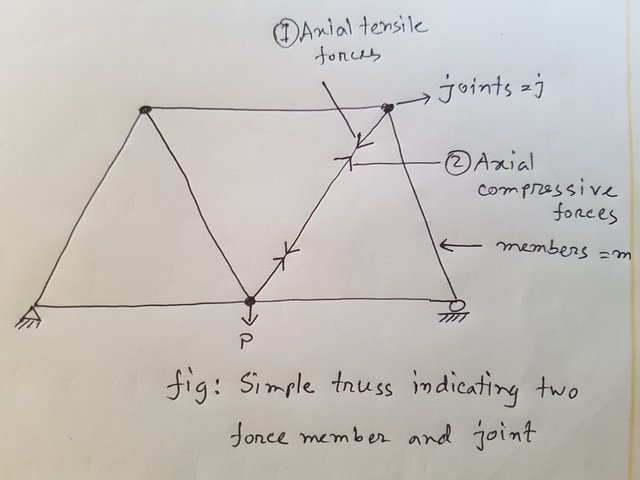
- Every member of truss is a two force member

*This is an image of some examples of truss made by us, the students, in the structure lab

Why the members are called two force members

Because the forces acting on a truss member are generally of TWO types-

1. Axial tensile force
2. Axial compressive force

Mathematical condition for Perfect Truss

m = no. of members in the truss
j = no. of joints in the truss

m + 3 = 2j ( Perfect truss)

m + 3 > 2j (Over rigid truss)

m + 3 < 2j (Collapsible truss)

Basic assumptions for Perfect Truss

1. The joints of a simple truss are assumed to be pin connections and frictionless.

2. The loads on the truss are applied on the joints only.

3. The members of a truss are straight two force members with two forces acting collinear with the center line of the members.

4. The weight of the members are negligibly small unless otherwise mentioned.

5. The truss is statically determinate.

Determination of Axial forces in the members of truss

There are TWO well known methods of determining Axial force of a member

1. Method of joints. ( summation of Fx = 0 ; summation of Fy = 0)
{here the two axial forces on the member is considered}

2. Method of sections. ( summation of Fx = 0 ; summation of Fy = 0 and summation of moment, M = 0)
{here two axial forces along with moment is considered}

THANKS EVERYONE, here is the source of the writings

Source: BEGINNER'S ENTRY TO ANALYSIS OF STATICALLY DETERMINATE STRUCTURE

[All figures are drawn or captured by author himself during practical lab classes and permits any reuse and republish of these images for any educational purpose]