Gravity and gravitational field, simple explanation.
All objects fall due to gravity, this has made the earth round and has also influenced various factors, but we do not know the exact definition of gravity.
Gravity is the name we give to the force of attraction that is exerted between objects, this is the definition although we do not fully understand it. Gravity affects all things and we also understand that it extends throughout the universe. In the chapter substudy, the basic behavior of gravity is examined.

Source
CC BY-SA 3.0
Gravity spreads throughout the universe, according to Isaac Newton, who got this idea when he was sitting under an apple tree. Newton understood the concept of inertia of Galileo, he knew that in the absence of external forces objects are kept in motion or in a straight line with constant speed. He also knew that any change in the speed or direction of an object is due to the action of a force.
Newton had been reflecting on the fact that the Moon does not describe a straight path, but, it revolves around the Earth and also that, a circular motion is an accelerated movement, which implies the presence of a force; this force was unknown. Newton had the insight to understand that the force acting between the Earth and the Moon is the same force that pulls all the apples and all the things that he called the force of gravity.
Source
public domain
The moon that falls?
This concept comes from Newton, who compared the apple that falls with the Moon. He realized that if the Moon did not fall he would move in a straight path away from Earth. His idea was that the Moon was falling around the Earth. Thus the Moon falls in the sense that it falls below a straight line, which would describe if no force were exerted on it.
Newton hypothesized that the Moon was nothing but a projectile spinning around the earth under the action of gravity. Newton compared the bullet of a gun with the Moon, that when being fired, formed a parabolic trajectory and if it fired with sufficient rapidity, the bullet would move on a circle, that is to say, in orbit.
Its tangential velocity between (parallel velocity component) is sufficient to guarantee movement around the earth. This idea to pass from hypothesis to scientific theory would have to be proven, its test consisted in verifying that the fall of the Moon below its straight path, was incorrect proportion, with respect to the fall of an apple or of any object that has a terrestrial surface.
Newton thought that the mass of the Moon would not affect its fall, in the same way that the mass does not affect at all the acceleration of objects in free fall, near the surface of the Earth. It is known that the Moon was sixty times farther from the center of the earth, than the surface than an apple on the surface of the Earth, the force that causes the apples to fall is the same as that which keeps the Moon in its orbit.
We can classify the forces in two large groups: forces by contact and forces at a distance. The gravitational interaction, together with the rest of fundamental interactions, is part of those forces that act at a distance. Currently, physicists use the concept of field to explain how all forces act at a distance, including gravity. In this publication, we will study the concept of gravitational field. Prepared?.
In a general way, we can say that a field is a region of space in which we assign to each of its points a value, either scalar or vectorial.
In Physics, it is very common for us to work with a particular type of field that is the field of forces. Although Newton discovered the force of gravity, he did not want to make any assumptions about how it was transmitted from one body to another. His phrase "et hypotheses non fingo" is famous, which could be translated as "I do not invent hypothesis". Hence, after his death, a key question would remain open that would occupy the minds of some of his successors: how can we explain the action at a distance? To solve this question, physicists introduce the concept of force field, developed in the nineteenth century by Faraday and Maxwell and later perfected by Einstein in the twentieth century.

Source
CC BY-SA 3.0
Intuitively we can say that a field of forces is a region of space whose properties are altered by the presence of a body that can originate interactions at a distance. Although Faraday and Maxwell elaborated their ideas to explain electromagnetic interaction, they suggest that their conclusions are extendable to the case of gravitational fields.
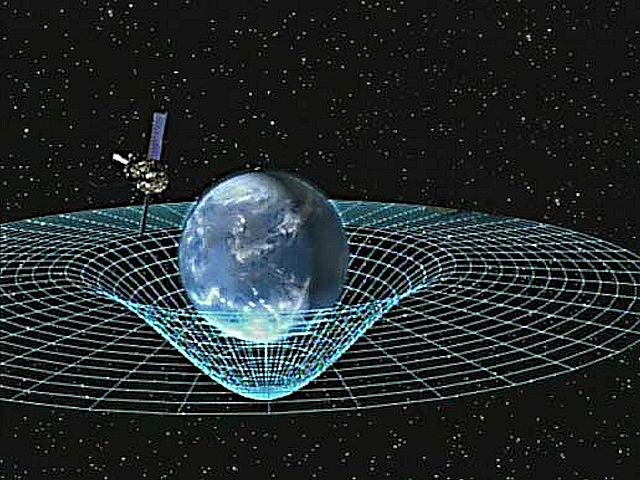
To analyze the concept of gravitational field, we must first understand what is gravitation or gravity: it is the attraction of bodies according to their mass (the physical magnitude that is responsible for reflecting the amount of body matter).
This gravitation is produced by the action of the force of gravity, a force that the planet Earth exerts on the bodies towards its center. The sector of space, at whose points the level of intensity of the force of gravity is defined, is known as a gravitational field.

Source
CC BY-SA 3.0
This is a field of forces that has the ability to represent gravitation. Suppose that, in a space X, a mass R is located. This mass, by the law of gravity, will generate a certain physical situation: the gravitational field. As for the intensity of the gravitational field, it can be measured according to the gravitational acceleration that the body acquires in this field.
It is important to note that the space around the mass R mentioned above has different characteristics depending on whether the mass is present or not: in this context, we say that its presence generates a gravitational field. In the same way, if we approached another mass to the first, we could appreciate a certain interaction between both.
Of course we can not guarantee the existence of this field around the first mass beyond the scope of speculation, because we can only appreciate the gravitational field once we approach the second mass, which is called test or witness.
A body, located at any point in space, produces a gravitational field that is identical to the quotient between the force of gravitational attraction that the element in question exerts on a witness mass that is in place and the value of the same mass witness.
The way to understand the gravitational field varies according to scientific theory. For relativistic physics, it is a second-order tensor field. In contrast, Newtonian physics considers the gravitational field as a vector field. According to one or another position, the field will be useful to solve different problems.
Precisely, the needs of each problem directly affect the way we treat the gravitational field. As indicated in the previous paragraph, according to Newtonian physics, it must be represented by a vector field, that is, an expression that associates a vector to each point (a physical quantity that consists of a length and an address).
One of the concepts necessary to understand the vector field is that of field lines, which serve to improve the visualization of a static vector field, either magnetic or electrostatic, among other options. In short, the use of these lines helps generate a map of the gravitational field and its appearance we can say that they are open.
For Newtonian physics, the definition of a gravitational field is the force that a given particle experiences if it is faced with a mass distribution, taking into account the unit of mass as a reference for the calculation. This leads us to conclude that it has the dimensions of an acceleration; however, scientists normally express their intensity in newtons per kilogram.

Source
public domain
We understand the tensor field, in which relativistic physics represents the gravitational field, to one in which a tensor is associated to each point of space (an algebraic entity that has more than one component, used for the generalization of the matrix, the vector, and the scalar so that they do not depend on a coordinate system).
REFERENCES
- https://study.com/academy/lesson/gravitational-field-definition-formula-quiz.html
- https://www.sciencealert.com/a-mathematician-has-proposed-a-way-to-create-and-manipulate-gravitational-fields
- http://www.gravity.co/
- https://spaceplace.nasa.gov/what-is-gravity/en/
- https://en.wikipedia.org/wiki/Gravitational_field
Hi @robertoromero
We have selected your post as post of the day for our DaVinci Times. Our goal is to help the scientific community of Steemit, and even if our vote is still small we hope to grow in quickly! You will soon receive our sincere upvote! If you are interested in science follow us sto learn more about our project.
Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.
CLICK HERE AND VOTE FOR DAVINCI.WITNESS
Keep in mind that for organizational reasons it’s necessary to use the “steemstem” and “davinci-times” tags to be voted again.
Greetings from @davinci.witness and the itaSTEM team.