Short Explain About: Dispersion and diffraction on fourier transforms

rickyxp (44)in #steemstem • 7 years ago

The Fourier transform, named after Jean-Baptiste Joseph Fourier (French mathematician who lived between 1768 and 1830), is an almost magical mathematical tool, capable of decomposing any periodic function (in time, or space) into a sum of functions of base of sinusoidal type (dependent of the frequency), or similar way to how a musical chord can be expressed in terms of the amplitudes (= volume) of each one its constituent notes.

The term Fourier transform refers not only to the transformation operation itself but also to the function it produces.

C major chord, (do+mi+sol) = (C+E+G)
Source

A good example is what the human ear does since it receives an auditory wave and transforms it, decomposing it into different frequencies (which is what is finally heard). The human ear perceives different frequencies as time passes, however, the Fourier transform contains all the frequencies of the time during which the signal existed; that is, in the Fourier transform a single frequency spectrum is obtained for the entire function. In short, the Fourier transform of a periodic function in time is basically the frequency spectrum of that function.

Source
Fourier transform between two functions.

The function f (x), (1), is time-dependent (red line). It is the sum of six sinusoidal functions with different amplitude but with harmonically related frequencies. The sum of these functions is called the Fourier series.

The Fourier transform f (ω), (2), (blue line) represents the amplitude vs. frequency and accounts for the six frequencies and their corresponding amplitudes.

(1)

Source
(2)

Source

The function (2) is the Fourier transform of the function (1)
Function (1) is the inverse Fourier transform of (2)

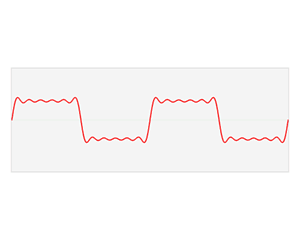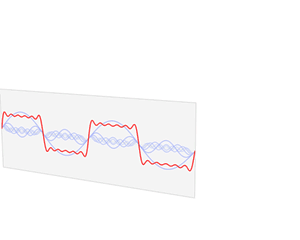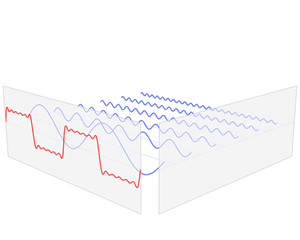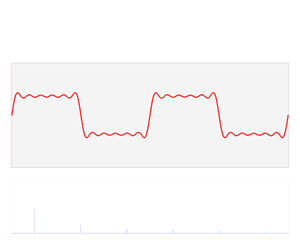
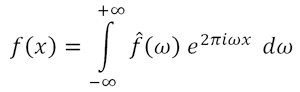
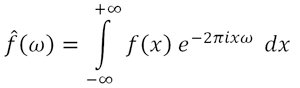
Each of these basic functions in which a function can be decomposed is a complex exponential with a different frequency (ω). Therefore, the Fourier transform provides us with a unique way of expressing any complicated function as the sum of simple sinusoids.

The inverse function to a Fourier transform is called inverse Fourier transform, also known as Fourier synthesis (or Fourier series), which is the way by which we can obtain any original periodic function from the sum of simple sinusoids