Source

Hi steemers, I'm going show a compilation of my research about one of the most important things in chemistry, The Pauli's Exclusion principle

I hope that this little research will help you!

Pauli's Exclusion principle states that in an atom can not have the same quantum number. This is an example of a general principle that applies not only to electrons but also to other half-integer spin particles (fermions). It does not apply to whole spin particles (bosons). The nature of the Pauli exclusion principle can be illustrated by the assumption that electrons 1 and 2 are in states "A" and "B" respectively. The wave function of the two-electron system would be:

Source

---

Source

---

This wave function is not acceptable because the electrons are identical and indistinguishable. To take this into account, a linear combination of the two possibilities must be used, since it is not possible to determine which electron is in which state.

The wave function for the state, in which the two states "A" and "B" are occupied by the electrons, can be written:

Source

---

Pauli's exclusion principle is part of one of our most basic observations of nature: particles of half-integer spin must have antisymmetric wave functions, and whole-spin particles must have symmetric wave functions. The minus sign in the previous relationship forces the wave function to disappear, if both states are "A" or "B", implying that it is impossible for two electrons to occupy the same state.

APPLICATIONS OF THE PAULI EXCLUSION PRINCIPLE

• Case number 1: NaCl Sodium Chloride

In this case, the sodium chloride molecule is formed by the ionization of the sodium and chlorine atoms and the attraction of the resulting ions, the sodium atom has 3 electrons out of a complete layer, and it takes only 5.14 electron volts of energy, to release that electron.

Chlorine lacks an electron to complete a layer and releases 3.62 eV when it acquires that electron (its electronic affinity is 3.62 eV). This means that when they are widely separated, only 1.52 eV of energy is needed to donate one of the electrons from sodium to chlorine.

When the resulting ions approach each other, their electric potential energy becomes more and more negative, reaching -1.52 eV at a separation of approximately 0.94 nm. This means that, if neutral sodium and chlorine atoms were found closer than 0.94 nm apart, they would be energetically favorable to transfer an electron of Na to Cl, and form an ionic bond.

Source

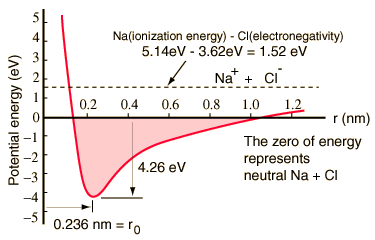
The potential energy curve shows that there is a minimum at a 0.236 nm separation and then a strong increase in the potential that represents a repulsion force. This repulsive force is more than just an electrostatic repulsion between the electron clouds of the two atoms, it has a quantum mechanical character based on the Pauli exclusion principle, and is often called simply "repulsion by exclusion principle". When the ions are widely separated, the wave functions of their main electrons do not overlap significantly, and they can have identical quantum numbers. As they get closer, the increasing superposition of wave functions causes some to be forced into higher energy states.

Two electrons can not occupy the same state so that when a new set of energy states is formed, a two-core system, lower energy states fill up and some of the electrons are pushed to higher states. This requires energy, and it is experienced as a repulsion, foreseeing that the ions can get closer to each other.

The potential diagram for gaseous NaCl and the environment is different in the normal solid state, where sodium chloride (common table salt) forms cubic crystals. The separation of ions is 0.28 nm, somewhat greater than that of the gaseous state.

An important part of the study of molecular structure is the description of chemical bonds that are formed between atoms. Classical studies are formed by the ends of the ionic bond in sodium chloride, and the covalent bond in the hydrogen molecule.

• Case number 2: The hydrogen molecule

The hydrogen molecule, is a clear example of a covalent molecule, is formed by the superposition of the wave functions of the respective electrons of hydrogen atoms, in an interaction that is characterized by an exchange of interaction. The character of this bond is completely different from the ionic bond that is formed in sodium chloride, NaCl. If the energy balance is then measured when the H + and H- ions are formed, and the attractive force between them is examined, the energy that is required is positive for any value of ion separation. That is, there is no distance in which there is a net attraction interaction, so the link cannot be ionic.

The distribution of the electrons around the protons of hydrogen is described by a quantum mechanical wave function, and the wave function that describes the two electrons of a pair of atoms can be symmetric or antisymmetric with respect to the exchange of identical electrons. By the Pauli exclusion principle, it is known that the wave functions of identical two fermions must be antisymmetric. The part of the wave function of the electron spin can be symmetric (parallel spins) or antisymmetric (opposite spins), but then the spatial part of the wave function must be opposite. This ensures that the full wave function (the product of the spin and space wave functions) is antisymmetric. The two possibilities for spatial wave functions for distant hydrogens are shown below.

Source

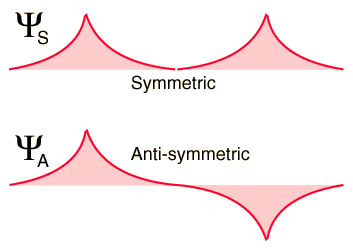
When the hydrogen atoms come together (as in the figure below), the symmetric spatial wavefunction leads to a configuration of bonding of the electrons, and the antisymmetric does not. The actual electronic charge density is given by the square of the magnitude of the wave function, and it can be seen that the symmetric wave function gives a high electron density between the nuclei, which leads to a net force of attraction between the atoms (Creates a link).

Source

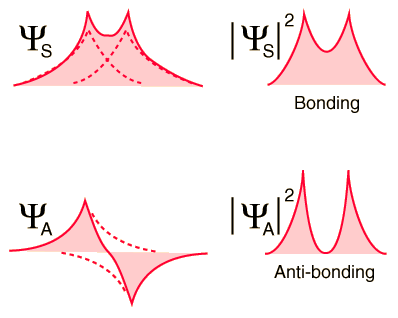
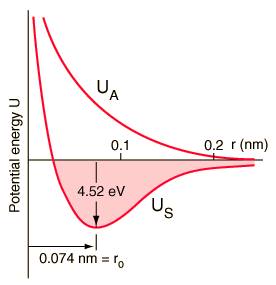
The exchange interaction (which is a quantum mechanical effect completely) leads to a strong bond of the hydrogen molecule, with a dissociation energy of 4.52 eV at a separation of 0.074 nm. The potential energy of the anti-binding orbital gives an idea of why a third hydrogen atom can not bind to the two atoms of the hydrogen molecule. It would be in an anti-binding situation with one of the other hydrogen atoms and therefore would be repelled. It is said that the bond in the hydrogen molecule is "saturated" because it can not accept another union anymore.

Source

• Case number 3: Layer model of the Nuclei

The visualization of a densely populated nucleus in terms of orbits and layers seems much less plausible than the layer model corresponding to atomic electrons. It is easy to believe that an atomic electron can complete many orbits without tripping over anything, but it would be expected that the protons and neutrons of a nucleus would be in a continuous process of collisions with each other. But dense gas-type nuclei models, with multiple particle collisions, do not fit the data, and also the remarkable patterns in core stability, such as "magic numbers," suggest an apparently unlikely structure layers.

With the enormous strong interaction acting between them and with so many nucleons colliding, how can they complete the nucleons, entire orbits without interacting? This has the characteristics of a process of the Pauli exclusion principle type, in which two fermions can not occupy the same quantum state. If there are no near-unfilled quantum states, which are within reach of the energy available for the interaction, it will not occur. This is essentially a quantum idea - if a "hole" is not available for a collision with a nucleon, then the collision will not occur. There is no classic analogy of this situation.

The evidence of a type of layer structure, and a limited number of allowed energy states, suggests that a nucleon moves in a kind of effective potential well, created by the forces of all the other nucleons. This leads to the quantization of energy in a manner similar to the potentials of the square well and the harmonic oscillator. As the details of the well determine the energies, many efforts have been devoted to the construction of potential wells for the modeling of the observed nuclear energy levels. The solution of the energies of said potentials gives a series of energy levels like the ones on the bottom left. The names of the levels are somewhat different from the corresponding symbols of the atomic energy levels. The energy levels increase with the quantum number of the orbital angular momentum l, and the symbols s, p, d, f ..., are used for l = 0,1,2,3 ... as well as for the atoms. But in reality there is no physical analogy with the main quantum number n, so the numbers associated with the level start right at n = 1 for the lowest level associated with a given orbital quantum number, giving symbols such as 1g, which It could not happen in the atomic labeling system. The quantum number of the orbital angular momentum is not limited to n as in the atomic case.

Source

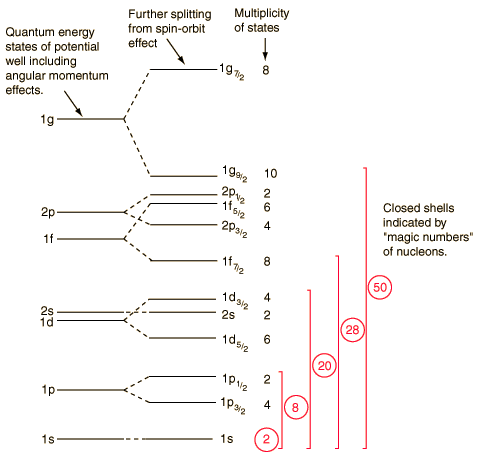
• Case 4: Influence of Pauli's Principle on Nuclear Models

The Pauli exclusion principle is involved in the basic explanation of the model of nuclear power state layers. The evidence of the layer structure in the nucleus was surprising at first because a dense collection of strongly interacting particles should be colliding with each other all the time, resulting in a redirection and perhaps a loss of energy from the particles. Pauli's principle effectively blocks the loss of energy, because only a nuclear particle can occupy a given energy state (neutrons and protons are fermions with spin 1/2). In this dense set of matter, all low-energy states will be full. This means that particles can not participate in interactions that would reduce their energy since there are no lower energy states to which they can go. A dispersion can occur by an external particle that raises the energy of a nucleon, but scattering that lowers an energy level is blocked by the principle of exclusion.

Pauli's principle is also invoked in the liquid drop model, and there is a term in the Weizsaecker formula for the binding energy that is attributed to the principle of exclusion. The filling of all the low energy states is contemplated in the model of the liquid drop, and that favors the condition A = 2Z (that is, the same number of protons and neutrons). Since the energy levels of neutrons and protons for certain quantum states are comparable, then a total lower energy can be obtained by filling both at the same level, instead of having one or more nucleons at higher quantum levels. The Pauli principle also favors an even number of neutrons and protons: the pairs of fermions are expected to have anti-parallel spin, and therefore do not contribute to the total spin. This is expressed by another term in Weizsaecker's formula.

For more Information Visit:

• https://en.wikipedia.org/wiki/Pauli_exclusion_principle
• https://www.thoughtco.com/definition-of-pauli-exclusion-principle-605486
• https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Electronic_Structure_of_Atoms_and_Molecules/Electronic_Configurations/Pauli_Exclusion_Principle
• Fundamentals of Chemestry, Romain Elsair