LIMITS!

mindhacks (52)in #steemstem • 7 years ago (edited)

Growing up you may have heard the phrase: “give it your 110%”, but is it possible to push yourself, or any system above 100%? The whole idea behind “giving your 110%” was used a motivational boost to break or surpass your current limits, because determining limits not only helps you surpass your own expectations but allows many mathematicians and scientist to discover innovative ways to advance technology further.

By definition; a limit is a point or level which something does not extend beyond, for example in probability, the probability of something occurring may never surpass 1 but cannot go below zero. That is; P(x): 0 <= x <= 1, or in other words “the probability of ‘x’ is in between and including 0 and 1”.

Media Source: http://longwallpapers.com/

In mathematics, the “limit” of some function f(x) is the value that some variable ‘x’ approaches over ‘time’ or some other variable y. Here’s another way to think of this; if I told you to drive 50 meters on my customized race track, you (the driver) would represent the variable ‘x’, and my race track would represent the function. As you approach 50 meters we can record all the positions you’ve landed on at any given time until you arrive at 50 meters.

This serves as a useful tool because we can hypothesize where you would be at any point, given some data, we could also determine where you would be if we told you to approach 100 meters, or 100,000 meters or even infinity meters. Assuming our customized race track follows some sort of determinable function, we can find the limit of you (x) going to infinity for our customized race track (f(x))!

Limits are applicable everywhere, in every field of study. In science we have physical limitations that prevent us from traveling faster than the speed of light or in technology our software may be limited by our present hardware. In mathematics we can take the idea of limits to infinity! Explicitly we take the limits of functions as they approach infinity. Sounds strange right? Actually no, taking limits of functions approaching infinity is a good way to determine the best / worst-case scenarios, or practicality for certain events.

A typical real-world infinity limit problem may look something like this: If I were to toss a coin infinite times, what is the probability that I will never get heads? If we we’re to rephrase that question in the form of asking a limit we could ask: “If I were to toss a coin n times, what is the probability P(n) that I have yet to toss a head?” Mathematically this would look like:

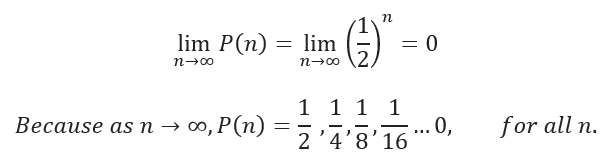
Notice that in our example the higher “n” becomes the closer our function gets to zero, therefore we can conclude that there is a probability of 0 from tossing a coin infinite times and not obtaining a head. This fundamental idea of limits is what forms the foundation for differential and integral calculus.

The concept of a derivative is the fundamental core of Calculus, if you’re a student taking Calculus 1 I presume you’re doing nothing but derivatives on trigonometric, or logarithmic functions. If you’re not a student taking Calculus do not worry, I will provide a simple definition and case use for derivatives! A derivative is simply a method of representing the rate of change. For example, we know that:

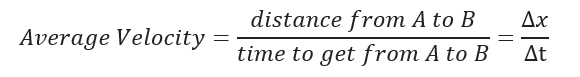
This is just a fancy, yet formal way to represent velocity. The fancy “triangle” symbol represents the Greek symbol “delta” which is used to describe a unit of change. We all know what velocity is, the average velocity of a car traveling at high way speeds may be anywhere from 96 Kph to 112 Kph, where kilometers represent distance, and hour represents time. Writing that formally we see:

See, nothing too difficult, right? Well now how do we apply the idea of derivatives? Remember the whole point of a derivative is to explain the rate of change behind a function, in this case the rate of change behind velocity. Applying a little bit of analytical thinking, if we derive our velocity function to obtain the rate of change what do we get? The velocity function describes how fast we are going over a given period, but it does NOT describe the rate of which we are increasing at. The rate in which our velocity changes is known as acceleration. Therefore:

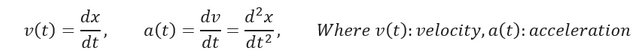
Don’t get intimidated by how this looks, literally all we are saying is that the rate of which velocity changes is known as acceleration. We can see this if we had some data and recorded each velocity difference over time. For example, suppose the following data represents a car traveling down the highway, here are the recorded velocities and times associated:

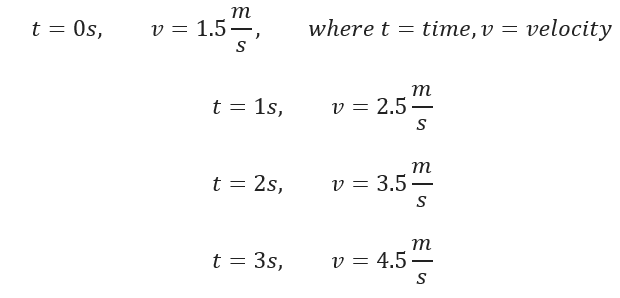
Evaluating the data, the rate at which the velocity changes every second is 0.5, thus acceleration is 0.5m/s^2! If we had a function f(x) that represented our velocity we could derive that using Calculus to obtain an acceleration function!

Tying everything together, the relationship that binds limits and derivatives is an interesting one. Ironically, we can actually “derive” the definition of a derivative and see that it is in fact a limit, a special case use of a limit:

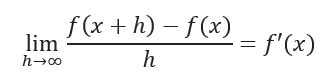
You can think of a limit as a more general concept when compared to derivative, as the definition of a derivative is derived from the concept of a limit!

TL;DR: Limits are defined to be a point that is intended to be impassable; consequently it is usually a system’s maximum or minimum point. We see limits and the applications of limits integrated in our everyday life; technology, automobiles, and humans; we all have our limits.

In math we can take the concept behind a limit, perform some algebra / calculus and determine the limits to any function. This proves to be a useful tool because if we had a function represent something extremely important; such as the time it takes for a nuclear reactor to melt down we could evaluate that function as it’s variable ‘x’ (may x represent time) approaches infinity to obtain a better understanding of when the nuclear reactor may melt down.

Limits are only the beginning and it helps form the foundation for differential and integral calculus. More specifically the formal definition of a derivative can be thought of as a special use of a limit. The general definition of a derivative in mathematics is a method that is used to describe the rate of change behind a function or system.

For example, if we evaluate the average velocity of a car traveling at highway speeds, the rate of which the car’s velocity is changing is known to be acceleration.

Therefore, if we derive a function that represents velocity we will obtain acceleration!

REFERENCES:

Note: A big thanks to @steemstem for providing fun and educational content relating to Science, Technology, Engineering and Math!