This set of equations is a computer.
Hilbert's Tenth Problem from his famous list published in 1900, asks whether it is possible to create an algorithm which solves every Diophantine equation, that is, one whose solutions must be integers.
The problem was solved, in the negative, seventy years later with the Matiyasevich–Robinson–Davis–Putnam, or "MRDP" theorem. This showed that all recursively enumerable sets are Diophantine.
To unpack that a little bit, what is a "recursively enumerable set"? It is a set of integers whose membership can be listed by a computer, or equivalent mechanism such as a Turing machine. The set of primes is recursively enumerable, for example. So is the set of x solutions to the Pell equation x^2 - 313y^2 = 1.
The set of Turing machines that halt is recursively enumerable! We can run all possible Turing machines in parallel (with larger machines being simulated at slower and slower rates.) Whenever a Turing machine halts, add it to the set. Every Turing machines that halts will eventually appear on the list. Now, we know from Turing's work that we can't write a program to decide in advance if a given Turing machine is in this set or not. All we can do is keep going and hope that our desired Turing machine shows up--- but we might wait forever.
The MRDP theorem tells us that every such recursively enumerable set can be represented as the solutions to a Diophantine equation, or a set of Diophantine equations. As an immediate consequence, this means that a computer program cannot tell if an arbitrary Diophantine equation has a solution. But we can do better and come up with a Diophantine equation that is universal, and can represent every other Diophantine equation or Turing machine!
James P. Jones, in the paper referenced below, gives the following concrete example of a set of equations which is undecidable:
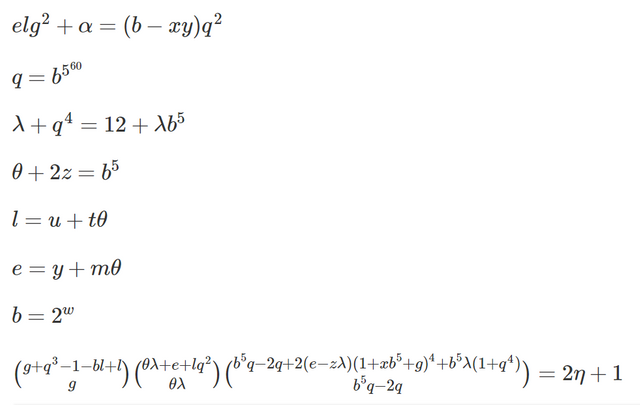
This set of equations has three parameters that define a recursively enumerable set: u,y, and z. (They can be reduced on one parameter, if desired.) These form a "program" for the equations. x corresponds to the input. The other nine variables b,e,g,l,m,q,t,w,α,η,θ,λ have integer solutions if and only if x is part of the recursively enumerable set.
The eight equations above have one exponent involving a variable, and three uses of the binomial coefficient function. These can be replaced by just multiplication and addition operations, at the cost of introducing additional variables.
Jones' equations are a general-purpose computer, of sorts. It doesn't tell you explicitly how to execute the program. It just guarantees that a solution exists, if and only if x is an output from the program (the recursively enumerable set) defined by the parameters u, v, y. It's a concrete counterexample to Hilbert's Tenth Problem, because if we could decide whether this equation had a solution we could solve the Halting problem, too.
References:
- "Diophantine Set" on Wikipedia
- "Hilbert's Tenth Problem" on Wikipedia
- James P. Jones, “Undecidable Diophantine Equations”, Bulletin of the American Mathematical Society, Volume 3, Number 2, September 1980. Download available here: https://pdfs.semanticscholar.org/7f96/11e582cf4a2efb1155c2fde9c891c6fc7be3.pdf
What a coincidence ... just some 15-30 minutes ago I was briefly reading on both Hilbert's Tenth Problem and recursively enumerable sets on Wikipedia, and next I randomly stumbled over your article here.
Congratulations @markgritter! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @markgritter!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV