En busca de que el idioma no sea una barrera para el conocimiento y este pueda llegar a todos, siguiendo la iniciativa que han tenido algunos integrantes de la comunidad de
#SteemSTEM he decidido traducir uno de mis artículos anteriores al idioma más popular de la plataforma, el inglés.
In order for language not to be a barrier to knowledge and can reach everyone, following the initiative of some members of the
#SteemSTEM community, I decided to translate one of my previous articles into English the most popular language of the platform.
I hope you all enjoy the following content, the original article can be found
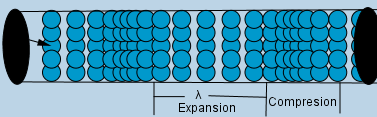
here. Let's remember that a mechanical wave of the longitudinal type is one in which the particles of the medium through which the wave propagates move in the same direction of propagation as this. A classic example would be a tube full of a fluid. Let's suppose that it is a gas, in the left end of the fluid we will have a piston which we will move with a simple harmonic movement. Its movement will cause the particles that make up the gas to move in the same way in simple harmonic movement.
The above can be seen exemplified in the GIF. The piston simulated by the arrow pushes the gas formed by its particle. We see how the wave propagates to the right and the particles move forward and backward in the same direction of propagation being a longitudinal wave. Something very interesting that we can observe is that there are areas where the particles are grouped and more cleared areas. This represents areas of higher and lower pressure respectively.
When the piston pushes the gas down, it compresses it. Decreasing its volume and causing the pressure to increase as the piston returns to its original position. The volume increases and the pressure decreases, these pressure changes spread throughout the fluid. If we make a comparison with the sine-wave we already know, the points of maximum pressure and minimum pressure are the points of zero displacement.
The longitudinal wave created here is governed by the wave function we studied earlier
. But when observing pressure changes it is convenient to express its behavior in these terms.
Sound waves are the cause of the effect we know as sound. These are longitudinal mechanical waves and they propagate from the source in all directions. When they propagate they create variations in the pressure in the environment above and below the atmospheric pressure with the same frequency of movement as the particles disturbed in the air, our ear works by detecting these pressure variations, the wave entering the ear creates these fluctuations and makes our eardrum vibrate, which translates into sound.
Due to the behavior of sound waves and the pressure fluctuations they create in the air, we can easily use equation
(3)
and related equations to describe them because they are also pressure waves. The sound waves with a high frequency have greater variations of pressure due to the fact that their wavelength is short and the maximum and minimum are closer. The frequency is also related to the tone that we know as high or low sound a high frequency is translated into a high sound and a low frequency into a low frequency. Also the greater the pressure amplitude the volume of the sound we perceive grows.
We know that the velocity of propagation of a wave is the square root of the quotient of the restitution force and the inertia that opposes it, in a fluid the restitution force refers to how easy or difficult it is to compress the fluid which is not said by the volumetric module and what complicates that our fluid returns to its state of equilibrium is the density of it. Therefore, the velocity of propagation of sound in a fluid is given by:
There are many phenomena related to waves and usually one of the most interesting is the Doppler Effect related to sound waves. It owes its name to the Austrian physicist Christian Doppler who was the first to describe it and it is
the apparent change in frequency that a wave undergoes due to the relative movement between the source and the observer.
Perhaps you think you have not perceived it at some time but, I assure you, yes.
There are several examples of the Doppler Effect. The most representative and daily is the one produced by cars. Those who have seen the Formula 1 (F1) have been in contact with it in a very clear way. That characteristic sound produced by cars as they approach the spectators until they pass in front of them and then move away is the Doppler Effect. It is the noise of the engines approaches we hear it more loudly and as we pass in front of us and then move away it becomes more intense. Following we will study this case of the Doppler Effect and some others.
Source at rest and receiver at rest:
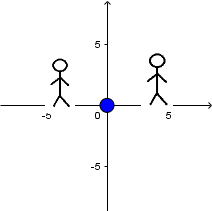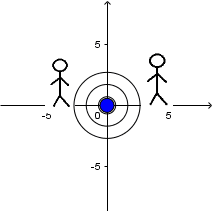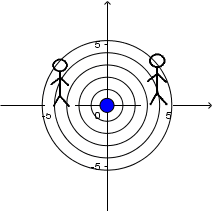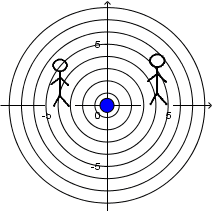
We can see a source at rest emitting sound waves and two observers, one to the left of the source and one to the right. As there is no relative movement between the source and the observers there is simply
no Doppler Effect.
So, that both receivers hear the sound at the original frequency of the source.
Source at rest and receiver in motion:
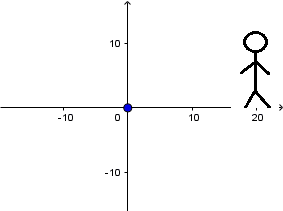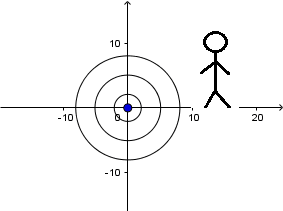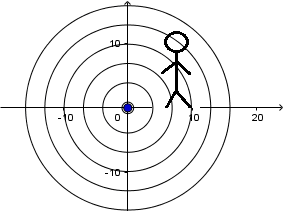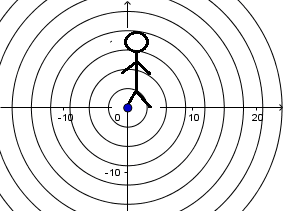
In the previous animation a source is observed at rest and a receiver that approaches it, the source emits waves with a frequency
f
and a constant wavelength given by
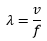
being v the speed of propagation of the wave in the middle. While the receiver is in movement, these waves arrive at it with a relative speed
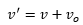
being
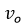
the speed of the observer. So the frequency
f'
that the receiver hears is given by:
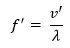
This results in:
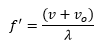
By replacing the Lambda value we get:
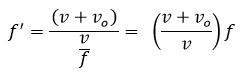
This frequency is higher than the original frequency emitted by the source.
Source in motion and receiver in motion:
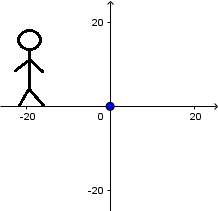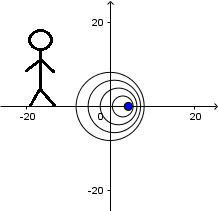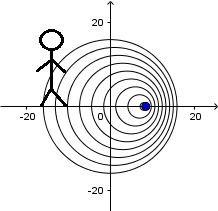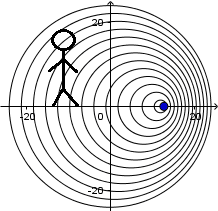
As we see here, things change the receiver and the source moves, the propagation speed of the wave is still v but the wavelength depends on the relative displacement between the source and the wave. Consequently, you can see the waves behind the source have a longer wavelength and those ahead have a shorter wavelength.
In front of the source the wavelength is:
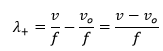
And behind the source:
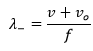
(2.1)
Knowing this, we can get the frequency that the receiver hears behind the source by replacing
(2.1)
in
(1.1).
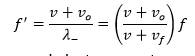
(3.1)
Moving source with slower speed than sound and receiver at rest:
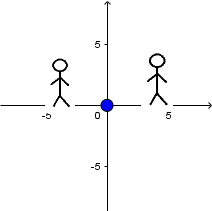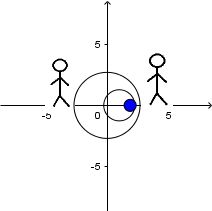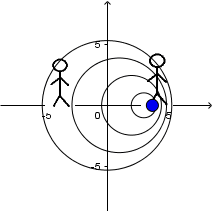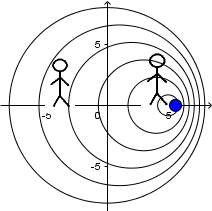
In the previous animation we have a source moving to the right and two observers; one behind the source and the other one in front of it. Using equation
(3.1)
we can get the frequency heard by these two observers and other cases we could imagine.
Proceeding for the observer behind the source:
Taking the equation (3.1)
and do it 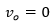 ., because the observer is at rest getting:
., because the observer is at rest getting:
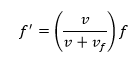
The frequency heard by this observer is less than the original frequency emitted by the source.
Proceeding for the observer in front of the source:
Similarly, we take equation
(3.1)
and do we do it
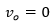
. The difference is that now, in the denominator we will have
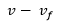
because the waves are emitted moving in the negative direction from the receiver to the source. We get:
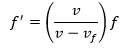
The frequency heard by this observer is higher than the original frequency emitted by the source.
Source moving at sonic speed and receiver at rest:
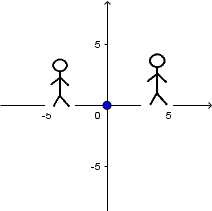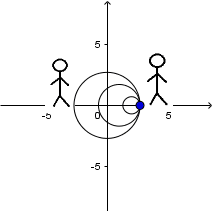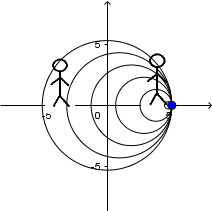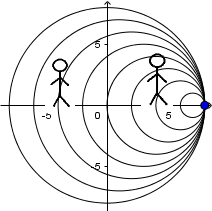
We have the same case above. The difference is that the speed of the source is equal to the speed of sound propagation in the medium, as you can see the waves in front of the source are all grouped at the same point next to the source so the observer in front of the source will not hear any sound until it is right in front of it.
Moving source with supersonic speed and receiver at rest:
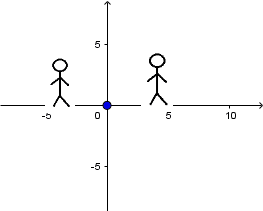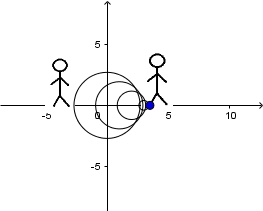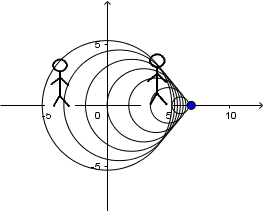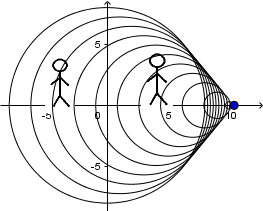
Since the speed of the source is faster than the speed of the sound propagation, the source is leaving the waves behind. An observer in front of it will not hear any sound until after the source passes in front of him. The cone that forms is known as the Mach cone and occurs when the source moves at supersonic speeds.
General conclusions:
• The particles in the longitudinal waves move in the same direction as the wave propagation.
• Sound waves are longitudinal and pressure waves.
• Sound waves propagate in all directions so they can be seen as spherical wavefronts.
• The frequency of a sound wave translates into the pitch of the sound we hear.
• A high frequency is a high-pitched sound and a low frequency is a bass sound.
• For the Doppler Effect to occur there must be relative motion between the source and the receiver.
• A receiver approaching the source hears a higher frequency than the original source.
• A receiver that moves away from the source hears a lower frequency than the one originally emitted by the source.
• If the source approaches the receiver, it will hear a higher frequency and a lower frequency if you move away.
• The Mach cone is produced at supersonic speeds.

I hope you've enjoyed reading about this topic and this interesting Doppler effect, if you want to read more science articles I invite you to visit the tag #SteemSTEM and #STEM-espanol.
(All the images and GIF's were made by me using GeoGebra Classic 5 mathematical software.)
References:
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Young, H. D, & Freedman, R. A. FISICA UNIVERSITARIA, volume 1. Pearson Educación de México, S.A. de C.V., 2009.
Tippens, P. E. FISICA - CONCEPTOS Y APLICACIONES. McGrawHill/Interamericana Editores, S.A. DE C.V., 7ma edition, 2001.

Credit @djredimi2 
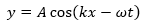 . But when observing pressure changes it is convenient to express its behavior in these terms.
. But when observing pressure changes it is convenient to express its behavior in these terms.
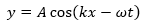
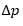 = y ; we define the known quantity as volumetric module:
= y ; we define the known quantity as volumetric module: 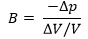
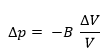
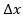 .
An area A and its volume is
.
An area A and its volume is 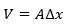 When the pressure changes its volume will be
When the pressure changes its volume will be 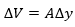 (compression).
(compression). 
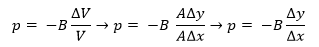
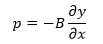

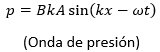
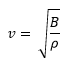 clearing B and replacing the above. We can rewrite the equation as follows:
clearing B and replacing the above. We can rewrite the equation as follows: 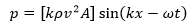

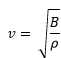

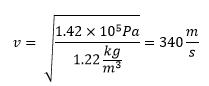
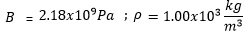
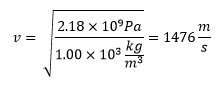


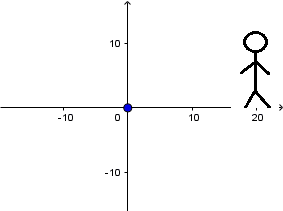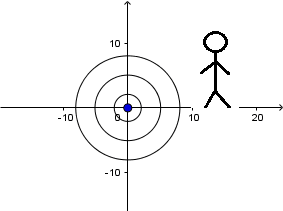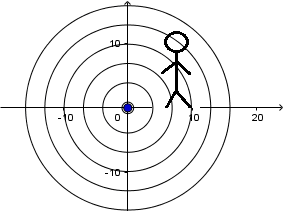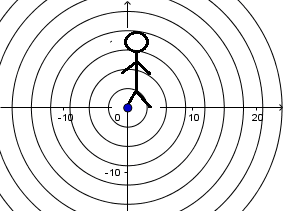
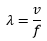 being v the speed of propagation of the wave in the middle. While the receiver is in movement, these waves arrive at it with a relative speed
being v the speed of propagation of the wave in the middle. While the receiver is in movement, these waves arrive at it with a relative speed 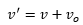 being
being 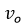 the speed of the observer. So the frequency
the speed of the observer. So the frequency 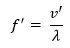
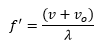
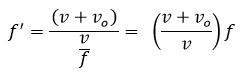
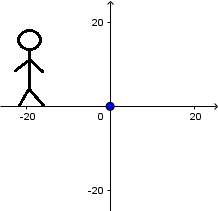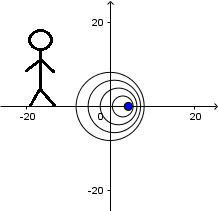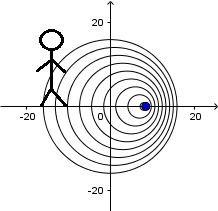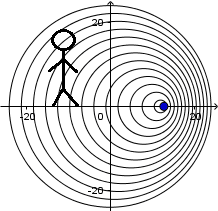
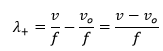
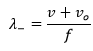
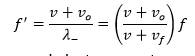

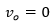 ., because the observer is at rest getting:
., because the observer is at rest getting: 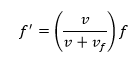
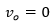 . The difference is that now, in the denominator we will have
. The difference is that now, in the denominator we will have 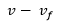 because the waves are emitted moving in the negative direction from the receiver to the source. We get:
because the waves are emitted moving in the negative direction from the receiver to the source. We get: 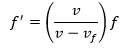

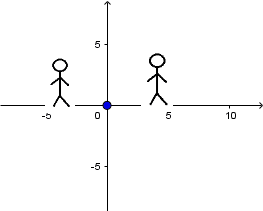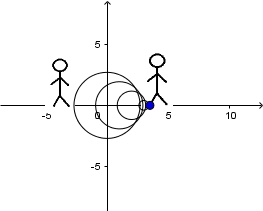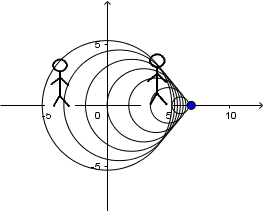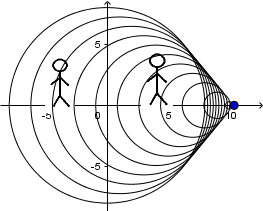


Thank you for your contribution. Dont forget to link references and sources when applicable!
=======================================================================================
This post was upvoted and resteemed by @Steemgridcoin with the aim of promoting discussions surrounding Gridcoin and science.
This service is free. Please follow @steemgridcoin if you want to support this initiative.
Have a nice day. :)