Basic terms of geometry: polygons
Polygons
In geometry, a polygon is a flat figure composed of a limited sequence of consecutive straight segments that close a region in the plane. These segments are called sides, and the points where they intersect are called vertices. The interior of the polygon is called an area. The polygon is the two-dimensional case of the polytope, a general geometric figure defined for any number of dimensions. In turn, a polydope of three dimensions is called polyhedron, and four-dimensional is called polychrome.
Source
Regular and irregular polygons
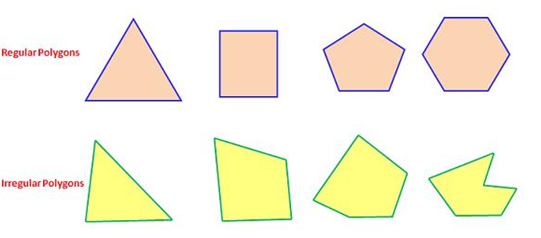
Polygons can be classified in different ways according to their characteristics. Regular polygons are those whose sides and their interior angles are equal. This means that all sides measure the same, as do the angles that form the joints of these segments.
These properties, on the other hand, make that all regular polygons are equilateral polygons (with sides of identical length) and equiangular polygons (the totality of their interior angles measure the same). In addition, the regular polygon can be inscribed in a circle; this means that it is possible to draw a circumference (called circumscribed) that passes through all its points, so that it contains it completely within it.
Source
An example of a regular polygon, therefore, is a square whose sides measure 5 centimeters each and its interior angles, 90 degrees each. Other regular polygons are equilateral triangles, regular hexagons and regular pentagons.
When their sides and their internal angles are not equal (that is, they do not have congruence with each other), we can speak of irregular polygons. On the other hand, if the internal angles and sides of the polygon are equal, the figure will be classified as a regular polygon.
In addition to the above, it is important to highlight that any irregular polygon is made up of the following elements:
-Inner angles.
-Inner point, which is the one that is within the perimeter of the polygon.
-Ventices, which are the points where the sides meet.
-Lands, which are the segments that come to delimit the perimeter of the mentioned polygon.
Due to its characteristics, it can be affirmed that the vertices of the irregular polygons can not be included in the same circumference. Like any other polygon, they can be named differently according to the number of sides: irregular pentagon (if it has five sides), irregular quadrilateral (four sides), irregular triangle (three sides), etc.
Convex and concave polygons
A concave polygon is one of the most interesting geometric figures that I have seen and of course a polygon of this type is not convex.
A simple polygon is concave if and only if at least one of its internal angles is greater than 180 degrees. An example of a non-simple (auto-intersection) polygon is a star polygon.
A concave polygon must have at least four sides.
A flat polygon is called convex if it contains all the segments that connect any pair of its points. Thus, for example, a regular pentagon is convex (left figure), whereas a pentagon indentation is not (right figure). A planar polygon that is not convex is said to be a concave polygon.
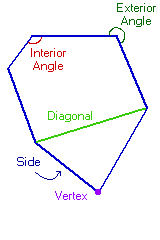
Elements of a polygon
These are the elements of a polygon:
• Side: one of the previously named segments that delimits the surface of the polygon.
• Vertex: point where two segments of those that make up the polygon join.
• Diagonal: segment that joins two non-adjacent vertices.
• Angle: opening of the two adjacent segments that concur in a vertex.
 Source
SourceClassification and construction of polygons
Regular polygons are the basis for many constructions, especially in the architectural field, but not only. In this section, you will find the constructions of different polygons. These constructions entail operations that are explained in each of the cases shown below.
The first row is intended for the construction of polygons having the length of the side as data, while the second row is collected constructions of the inscribed polygons.
For the best organization of contents, both triangles and quadrilaterals (polygons of 3 and 4 sides, respectively), we will study them separately from the rest of the polygons.
This space will increase with new routes. Each path has a link to its explanation.
Distribution
Pentagons from the side
- Regular Pentagon Polygon with 5 equal sides and 5 vertices of the same value.
- Regular hexagon. Polygon with 6 equal sides and 6 vertices of the same value.
- Regular heptagon. Polygon of 7 equal sides and 7 vertices of the same value.
- Regular octagon. Polygon with 8 equal sides and 8 vertices of the same value.
- Regular enegon. Polygon with 9 equal sides and 9 vertices of the same value.
- Decónono regular. Polygon with 10 equal sides and 10 vertices of the same value.
Registered polygons
- Pentagon registered. Regular polygon of 5 sides, but that is inscribed in a circumference. The data provided is the radius of the circumference.
- Hexagon enrolled. Regular polygon of 6 sides, but that is inscribed in a circumference. The data provided is the radius of the circumference.
- Registered heptagon. Regular polygon with 7 sides.
- Engraved octagon. Regular polygon with 8 sides.
- Engraved Enegon. Regular polygon of 9 sides.
- Decagon registered. Regular polygon with 10 sides.
Construction of an octagon
This first construction of a regular octagon is very simple.
1-. We draw a square and then its two diagonals. These two diagonals are cut in the center of the square.
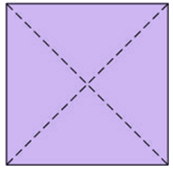
2-. Now draw the midpoint of each of the four segments that go from a vertex to the center of the triangle, drawing for each of them the segment perpendicular to it that passes through said midpoint. Each of these segments will cut to two sides of the square at its midpoints.
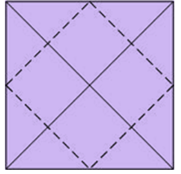
3-. For each of these cut points with the sides we draw the bisector of the angle that forms the segment calculated before and the side of the square to which it cuts (in dashed line).
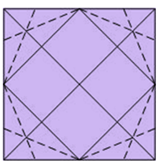
4-. These bisectors are cut into four points, which together with the four midpoints of the sides of the square form a regular octagon.

Images made by me
Quadrilaterals
Quadrilaterals are four-sided polygons. The most common are squares and rectangles, but there are many others. Like triangles, they are classified by their angles and their sides.
The most common quadrilaterals are the following:
- Parallelograms
The parallelogram, the geometrical figure that will occupy us next, is a type of quadrilateral although it is particular, since its sides are parallel two to two, that is, its opposite sides are parallel to each other.
There are different types of parallelograms, the rectangle parallelograms, which are characterized because all their internal angles are straight, that is they measure 90 ° and the parallelograms are not rectangles, which have two acute internal angles and the other two internal ones are obtuse. When the angle is obtuse it is because it measures more than 90 ° but is less than 180 °.
Now, enter the first, the rectangle parallelograms, we find the square and the rectangle and in the non-rectangles highlight the diamond and rhomboid.
The square is distinguished from the rest by presenting four equal sides and four right angles, also has four axes of symmetry, four edges and four vertices.
For its part, the rectangle, another popular parallelogram, has four sides that make right angles and their opposite sides have the same length. In this sense it differs from the square because only these opposite sides have a similar length, in the square all sides have the same extension.
On the side of the rhombus also its four sides observe the same length while the opposite interior angles will be equal. And the rhomboid is halfway to the rhombus and the rectangle, with its angles and also its sides identical from two to two.
For more information visit the following links:
I love geometry. upvoted
Thanks for information, been so long since I have been in school, I have forgotten most of this.