MATHEMATICAL EXPLANATION PARTE II- DEVELOPMENT OF THE FOURIER SERIES
Hello friends !
Continuing with my publications on the mathematical explanation, in this publication I will refer to the development of the Fourier series, in the previous chapter talk about the basic concepts, today I will talk about what is the function of the Fourier series, its definition, Theorem that defines it and we will also talk about the applications of Fourier, a video is presented at the end of this publication where the importance of this mathematical procedure for all of us is described with greater clarity.

"There can not be a more universal and simple language, more devoid of errors and obscurities, and therefore more apt to express the invariable relations of natural things. Mathematics seems to constitute a faculty of the human mind destined to compensate for the brevity of the life and the imperfection of the senses. "
Joseph Fourier
Fourier series
A series of Fourier is an infinite series that converges punctually to a periodic function and continuous to pieces (or by parts). The Fourier series is the basic mathematical tool of Fourier analysis used to analyze periodic functions through the decomposition of this function into an infinite sum of much simpler sinusoidal functions (like combination of sines and cosines with whole frequencies). The name is due to the French mathematician Jean-Baptiste Joseph Fourier, who developed the theory when he studied the heat equation. He was the first to study such series systematically, and published his initial results in 1807 and 1811. This area of research is sometimes called harmonic analysis.
It is an application used in many branches of engineering, as well as being an extremely useful tool in abstract mathematical theory. Areas of application include vibratory, acoustic, optical, image and signal processing, and data compression. In engineering, for the case of telecommunications systems, and through the use of the frequency spectral components of a given signal, the design of a system for the carrier signal thereof can be optimized. Refer to the use of a spectrum analyzer.
The Fourier series have the form:
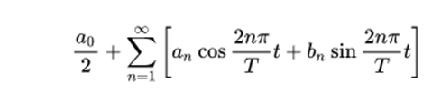
Where 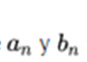 and are called Fourier coefficients of the Fourier series of the function f (t)
and are called Fourier coefficients of the Fourier series of the function f (t)
Definition
If f (t) is a function of real variable t, which is integrable in the interval 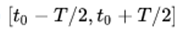 then the Fourier series development of f can be obtained in that interval. Outside the interval the series is periodic, with period T ,. If it is periodic in the whole real line, the approximation by Fourier series will also be valid in all values of t ,. Then the Fourier series associated with f (t) is:
then the Fourier series development of f can be obtained in that interval. Outside the interval the series is periodic, with period T ,. If it is periodic in the whole real line, the approximation by Fourier series will also be valid in all values of t ,. Then the Fourier series associated with f (t) is:
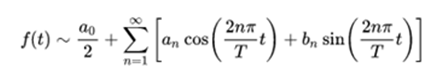
Where 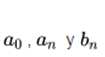 are the Fourier coefficients that take the values:
are the Fourier coefficients that take the values:
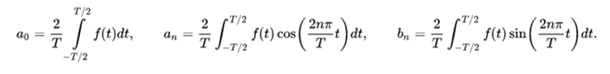
Because of Euler's identity, the formulas above can also be expressed in their complex form:
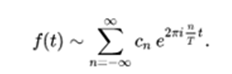
The coefficients would now be:
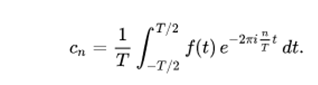
Another way to define the Fourier series is:
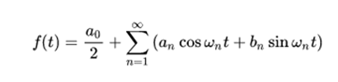
where 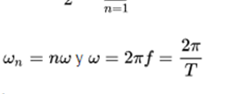
being :
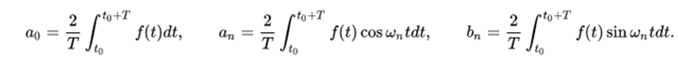
This form of the Fourier series is known as the Fourier trigonometric series.
Dirichlet's Theorem: Convergence to a periodic function
Suppose that f (x) is a periodic function, piecemeal and bounded, that in a period has a finite number of local maximums and minima and a finite number of discontinuities, of period 2p. Sean
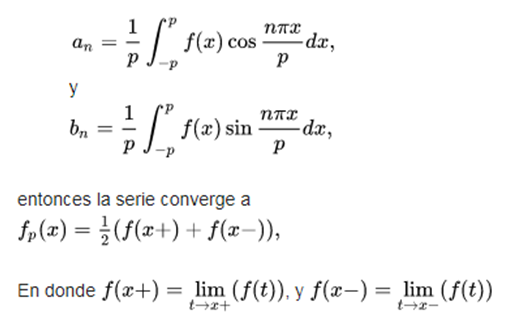
Examples of Fourier series
Let's see an example:
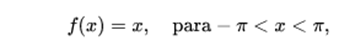
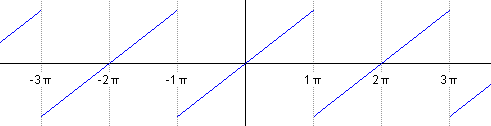
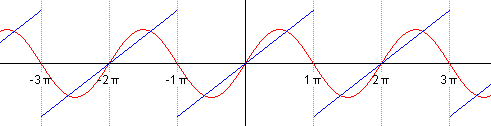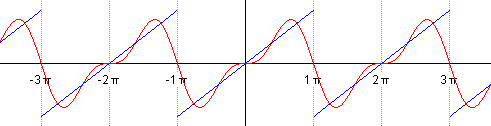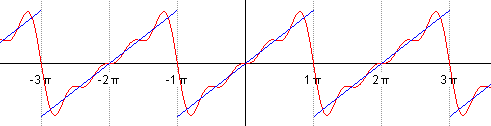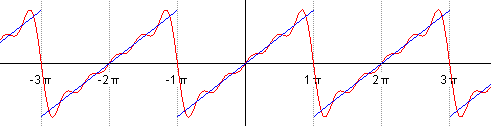
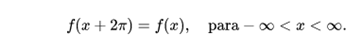
In this case, the Fourier coefficients give us this:
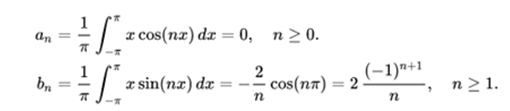
If the Fourier series converges towards: ƒ (x) of each point x where ƒ is differentiable:
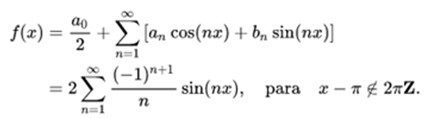
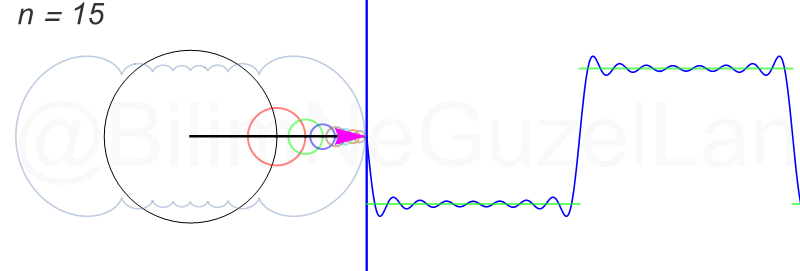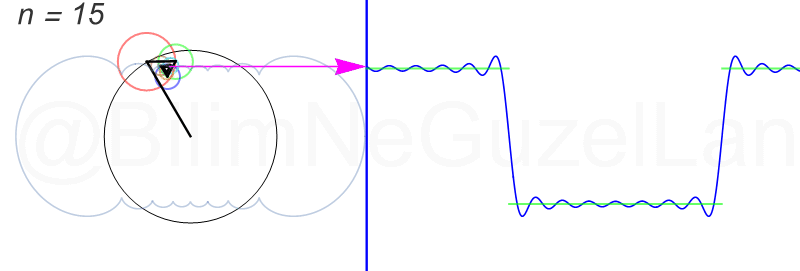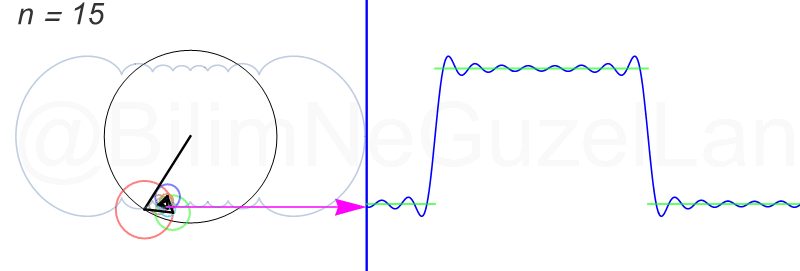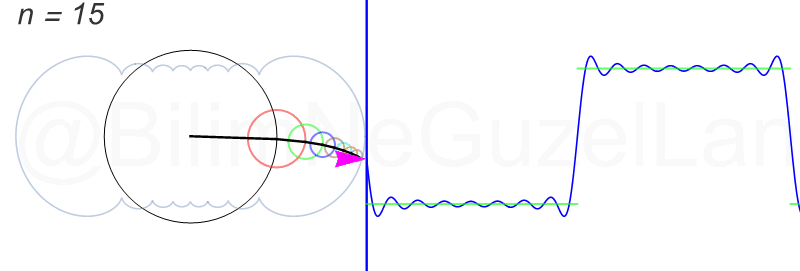
Applications of the Fourier series
- Generation of current or voltage waveforms
electrical by means of the superposition of sinusoids generated by variable amplitude electronic oscillators whose frequencies are already determined. - Analysis of the harmonic behavior of a signal.
Reinforcement of signals. - Study of the response in time of an electrical circuit variable where the input signal is not sinusoidal or cosinusoidal, through the use of Laplace transforms and / or solution in sinusoidal permanent regime in the frequency domain.
- The resolution of some differential equations in partial derivatives admit particular solutions in the form of easily computable Fourier series, and that obtain practical solutions, in the theory of heat transmission, the theory of plates, etc.
chapter 1
References
Lejeune-Dirichlet, P. "Sur la convergence des seéries trigonométriques qui servent à représenter une fonction arbitraire entre des limits données". (In French), transl. "On the convergence of trigonometric series which serve to represent an arbitrary function between two given limits". Journal f¨ur die reine und angewandte Mathematik, Vol. 4 (1829) p. 157-169.
"Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" About the representability of a function by a trigonometric series. Habilitationschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Gotinga, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind (in German). Archived from the original on May 20, 2008. Retrieved on May 19, 2008.
Bibliography
- M. R. Spiegel, J. Liu, L. Abellanas (2003): Formulas and tables of applied mathematics. Second edition. Schaum series. Mc Graw-Hill.
- Fetter, Alexander L .; Walecka, John Dirk (2003). Theoretical Mechanics of Particles and Continued. Courier Corporation. pp. 209, 210.
https://es.wikipedia.org/wiki/Serie_de_Fourier
Spanish text: Una serie de Fourier es una serie infinita que converge puntualmente a una función periódica y continua a trozos (o por partes). Las series de Fourier constituyen la herramienta matemática básica del análisis de Fourier empleado para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones sinusoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier, que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicó sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces análisis armónico.
Google translate: A series of Fourier is an infinite series that converges punctually to a periodic function and continuous to pieces (or by parts). The Fourier series is the basic mathematical tool of Fourier analysis used to analyze periodic functions through the decomposition of this function into an infinite sum of much simpler sinusoidal functions (like combination of sines and cosines with whole frequencies). The name is due to the French mathematician Jean-Baptiste Joseph Fourier, who developed the theory when he studied the heat equation. He was the first to study such series systematically, and published his initial results in 1807 and 1811. This area of research is sometimes called harmonic analysis.
Identical to your text if I am not wrong