THE PHYSICS BEHIND CHARGE AND FIELD
The spark that jumps across a gap of 5 cm or so in a Van de Graaff generator is the dramatic effect of static electricity. Less conspicuous, but the cause of many problems in microelectronic circuits, are the tiny quantities of charge they build up and jump only a few micrometres. Many items of equipment that we rely on every day are controlled by microelectronic devices – just think of telephones, radio and television, traffic lights, domestic appliances such as washing machines and freezers, control systems in all forms of transport systems, railway signalling and aircraft control. On top of this, there is all the computer equipment in use. It is very important that these devices are not made unreliable by electrostatic effects.
The amount of charge that can damage circuits is very small – fractions of a microcoulomb are enough. The relatively small voltages that do damage are easily reached with everyday activities. Shifting position on a foam-filled chair can generate 1500 volts in a humid atmosphere and up to 18000 volts if it is very dry. Just walking on some carpets can generate up to 35 000 volts: that’s why you may feel a shock when you touch a metal door handle!
Voltages of this size would certainly destroy sensitive microelectronic circuits. So, built into the design of equipment are means to protect their delicate microelectronics from static electricity. It is no wonder that microelectronics engineers earth themselves before going near a circuit board!
Most objects in the world around us consist of matter in which charge is balanced, and to the surroundings such matter is electrically neutral. However, the forces between the charges within materials are responsible for the strength of the materials and all their mechanical and electrical properties. Charged bodies exert forces on each other: some are pulled towards each other and some are pushed away from each other. This is because there are two types of charge – we call them positive and negative. Their action can be summarised as: Like charges repel, unlike charges attract.
In this post, I will consider these charges in more detail. Of particular importance are the electric fields that charge produces, and the movement of charge from one place to another. I then go on to consider capacitors and finally show the similarity between the equations for an electric field and the equations for a gravitational field.
ELECTROSTATIC FORCES
Atoms are made from tiny negatively charged particles called electrons, and larger positively charged particles called protons. Each carries the same (yet opposite) quantity of charge. The charges are responsible for the electrostatic behaviour of materials. Atoms (except hydrogen) also contain neutral particles called neutrons. When two materials rub together, a few atoms of one material lose electrons, becoming positively charged. These electrons ‘stick’ to atoms on the other material, giving it a net negative charge. (In a television, a beam of electrons strikes the screen. You are aware that negative charge has built up if you touch the screen and hear a crack.)
A very important property of electrostatic forces is that they act at a distance. Hair or fur can be raised if a charged object (such as a comb) is brought near. Any charged body in the space around another charged body is acted on by an electric field, and will ‘feel’ a force. The direction of the force depends on whether the charges are alike or unlike. The size of the force depends on the size of the charges and their distance apart. The behaviour of electric fields is very similar to that of gravitational fields. It is easiest to begin with uniform fields.
UNIFORM ELECTRIC FIELD
The field between two parallel charged plates is uniform. When a charged body such as charged foil on an insulated handle is held in the space between such plates, the foil is deflected, since a force acts on the foil to make it move. The amount of the foil’s deflection is a measure of the field strength, and is the same at any point between the plates: the field is uniform.
The strength of the field is defined as the force on each coulomb of charge i.e electric field strength = force in newtons on a charge of one coulomb. Electric field strength is measured in newtons per coulomb (NC-1).
If a charged body is free to move, then it will move in the field – the field does work on the body and the charged body gains energy as it accelerates between the plates. When the separation of the plates is d metres, then the work done by a force of F Newtons in moving the charge from one plate to the other will be: F × d (joules)
The work done by the field is equal to the energy gained by the charge. If the potential difference (p.d.) across the plates is V volts, then the energy gained by Q coulombs will be: Q coulombs × V joules per coulomb = QV joules
Therefore: Fd = QV and rearranging this gives: F/Q = V/d
We now have an alternative and very useful way of measuring the strength E of an electric field: E is measured in newtons per coulomb or volts per metre.
EXAMPLE
Estimate the electric field between the ‘points’ of a spark plug.
ANSWER: First, estimate the distance between the points. This is usually very small, say 0.5 mm. The voltage across the points will be about 3000 V. So,
Electric field strength: E = V/d = 3000 volts / 5 × 10-4 m = 6 × 106 Vm-1
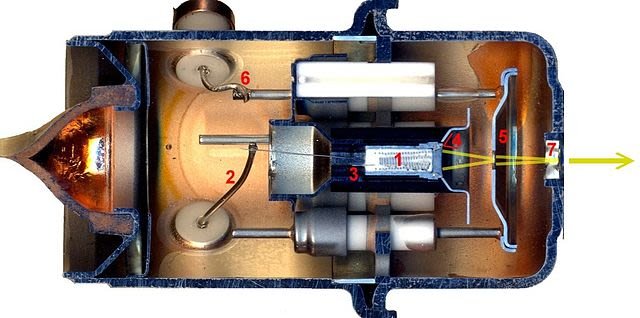
THE ELECTRON GUN AND ELECTRONVOLTS
Television tubes, cathode-ray oscilloscope tubes. X-ray tubes and electron microscopes are all devices that use beams of electrons. The electrons come from the heated wire filament of an electron gun. In the figure, there is a simple electron gun in which the filament is also the cathode. Electrons with enough energy escape from the surface of the wire, in thermionic emission. The large p.d. between the filament and a cone, the positive anode generates an electric field, and the electrons are attracted to the anode. Between the filament and the anode, they accelerate, gaining kinetic energy from the electric field. If m and e are the mass and charge of the electron, then:
Kinetic energy gained = Energy from electric field
½ mv2 = eV
where v is the speed of the electron after it has been accelerated through p.d. of V volts.
The energy gained by the electron is eV joules or V electronvolts. One electronvolt is the energy gained by a particle carrying a charge of 1.6 × 10-19 coulombs after it has been accelerated through a p.d. of one volt. The electronvolt is a more convenient unit of energy than the joule when we are dealing with the energies of particles on an atomic scale.
EXAMPLE
Calculate the velocity of a 5 MeV alpha particle, which has a mass of 6.646 × 10-27 kg.
ANSWER: The energy of the alpha particle is all kinetic energy, therefore:
½ mv2 = 5 MeV
To carry out this calculation the energy must be in joules:
5 MeV = (1.6 × 10-19) × (5 × 106) = 8.0 × 10-13 J
We can now write:
0.5 × (6.646 × 10-27) × v2 = 8.0 × 10-13
v2 = 8.0 × 10-13 / 0.5 × (6.646 × 10-27)
v = 1.6 × 107 ms-1
THE CHARGE ON THE ELECTRON – MILIKAN’S EXPERIMENT
In 1917, Robert Millikan, an American physicist, devised a clever way of measuring the charge on the electron. He sprayed tiny oil droplets between two parallel charged plates and watched their motion carefully through a microscope. We find with Millikan’s apparatus that many of the oil droplets become charged as they are forced through the tiny hole of the spray. Most of the charged droplets are negative and these experience a force in the electric field between the plates. All the oil droplets are acted upon by gravity and by the buoyancy force of the air.
By carefully adjusting the voltage across the plates, Millikan was able to make some of the charged droplets stand still. Then, he knew that the resultant force on such a droplet was zero. The weight of the droplet and the resistance due to air molecules were balanced by the electric force on the droplet. And, according to Stokes’ law, the force F acting on a spherical oil droplet of radius r which is moving with velocity v through a medium of viscosity η is given by:
F = 6πrηv
For oil of density ρ, the mass of the drop will be:
mass = 4/3 πr3ρ
and its weight:
4/3 πr3ρ g
There is an upthrust acting on the droplet equal to the weight of the air displaced:
Upthrust = 4/3 πr3ρAg
where ρA Is the density of air.
Millikan observed many droplets, carefully measuring the voltage required to give a constant velocity for each droplet. From his measurements he was able to calculate the smallest charge on a droplet. This was 1.6 × 10-19 C. He also discovered that other charged droplets carried either the same amount of charge or a whole-number multiple of this charge. He concluded that 1.6 × 10-19 C was the smallest possible charge and that it must be the charge on one electron.
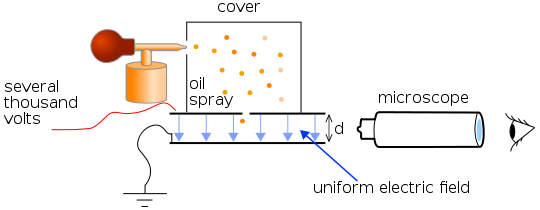
Simplified scheme of Millikan's oil drop experiment. Theresa Knott, CC BY-SA 3.0
DIRECTION OF THE ELECTRIC FIELD
A charged foil between two parallel plates is deflected in the same direction wherever it is placed between the plates – that is, the electric field has a direction. If the p.d. across the plates were reversed, the direction of the field would also be reversed and the foil would be deflected in the opposite direction.
The direction of the electric field between the plates is the direction of the force on a positive charge, that is, from positive to negative. The direction of any electric field is the same; the idea can even be used to describe the field around an isolated charge. Lines are used to describe the field, as indicated by small particles in the figure. A field line represents the orientation of the force and the arrow shows the direction of the force (positive to negative). The strength of the field is shown by the spacing of the lines – the closer they are, the stronger the field. Between the parallel plates, they are evenly spaced, indicating a field of uniform strength.
I will like to stop here for now. I will continue from here next time, but till then I still remain my humble self, @emperorhassy. Thanks.
REFERENCES
https://www.physicsclassroom.com/class/circuits/Lesson-1/Electric-Field-and-the-Movement-of-Charge
https://www.khanacademy.org/science/physics/electric-charge-electric-force-and-voltage
https://www.britannica.com/science/Coulomb-force
https://en.wikipedia.org/wiki/Electrostatics
https://www.thoughtco.com/definition-of-electrostatic-forces-604451
https://www.sciencedirect.com/topics/mathematics/uniform-electric-field
https://opentextbc.ca/physicstestbook2/chapter/electric-potential-in-a-uniform-electric-field/
https://electronics.howstuffworks.com/question694.htm
http://www.schoolphysics.co.uk/age14-16/Atomic%20physics/text/Electron_gun/index.html
https://en.wikipedia.org/wiki/Electron_gun
https://www.sciencedirect.com/topics/earth-and-planetary-sciences/electron-guns
https://courses.lumenlearning.com/physics/chapter/19-1-electric-potential-energy-potential-difference/
http://ffden-2.phys.uaf.edu/212_fall2003.web.dir/Ryan_McAllister/Slide3.htm
https://www.britannica.com/science/Millikan-oil-drop-experiment
https://en.wikipedia.org/wiki/Oil_drop_experiment
https://courses.lumenlearning.com/introchem/chapter/millikans-oil-drop-experiment/
https://en.wikipedia.org/wiki/Electric_field
https://www.siyavula.com/read/science/grade-11/electrostatics/09-electrostatics-03

This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.