THE LAWS OF THERMODYNAMICS: An Adiabatic Change of a Gas and The Second Law of Thermodynamics.
When a gas is
compressed very rapidly, there is no time for energy to leave the gas by thermal processes and go to the surroundings. But the temperature changes because work is done – temperature increases for a compression. The change is caused by an external
force, so there will be an increase in pressure. This rapid change of volume is called an adiabatic change (no thermal transfer of energy). It is the opposite case to compressing very slowly where the gas remains at a constant temperature.
A common example of a process that is almost adiabatic is the compression of air in a bicycle pump. The mechanical work done in compression increases the internal energy of the air and so its temperature rises. If this is done very quickly, the energy does not have time to escape thermally through the walls of the pump.

Image of adiabatic process. User:Stannered, GNU Free Documentation License
There is also an adiabatic change when the gas is thermally isolated from its surroundings by an insulated wall preventing all thermal transfer. This contrasts with the isothermal case where the gas is contained by a wall that is a good thermal conductor of energy.
Zero thermal transfer is a very precise state, so what happens to an ideal gas in an adiabatic change is also precise. It is that:
pVγ = a constant
where γ is the ratio of the principal specific heats of the ideal gas, Cp/Cv: γ is a constant. This equation provides an important relationship between p and V during the change. In addition, it can be used with the ideal gas equation pV = nRT, so that it also provides relationships between T and p and between T and V during the change. It is an example of an exceptionally useful result in physics, used by practising physicists who take for granted the derivation. I do not need to prove the equation here.
I have now looked at different changes of volume that can occur to an ideal gas: change of volume at constant pressure, change of volume at constant temperature and change of volume with no thermal transfer. These are compared on a pV diagram for a decrease in volume from the same starting volume.
THE SECOND LAW OF THERMODYNAMICS
We saw from the first law that the change of internal energy of a system is related to the sum of the energy transferred to it thermally and to the work done on the system. We have also seen how work can increase internal energy. So far, I have avoided discussing how to transfer internal energy to work. We find that we can transfer some of the energy to work, but not all of it. This gives rise to the second law of thermodynamics. One of several alternative statements for the law is:
Version 1 of the second law states that it is impossible for thermal energy to transfer from a high temperature source to do an amount of work equivalent to that amount of thermal energy.
The industrial importance of this version of the second law is immediately obvious. Coal, gas or oil is burnt in a boiler in a power station to provide large quantities of thermal energy. This energy is transferred to energy within turbines and finally to energy used in the home. It is not possible for all the energy from the fuel to be transferred completely into work via the turbines.
It is a consequence of the second law that some energy is transferred to a reservoir of energy at a lower temperature than the temperature of the boiler. This reservoir may be the surrounding atmosphere or the water in a cooling system such as a river. There is no way of avoiding this transfer of lost thermal energy. Engineers have put a lot of effort into designing more and more efficient engines to do work but as we shall see, there is an efficiency limit that arises from the second law.
There is an important alternative statement of the law:
Version 2 of the second law states that t is not possible to have a thermal transfer of energy from a colder to a hotter body without doing work.
If the law did not apply, it would be very easy to take thermal energy from our garden and use it to heat the house in winter, and to do this without limit. We can transfer energy from a colder to a hotter body (or reservoir) but it is necessary to do some work. Both refrigerators and heat pumps do this.
HEAT ENGINES: THE INTERNAL COMBUSTION ENGINE
Engines are designed to do work. The type of engine with which we are most familiar is the car engine, which uses the thermal energy produced by igniting petrol. It is called an internal combustion engine.
Air and fuel are mixed during the intake stroke. After the intake valve is closed, the air and fuel mixture is compressed as the piston goes through the compression stage of the cycle. The spark plug ignites the mixture and this produces the expansion, which is the part of the cycle producing the power. Finally, spent gases are expelled through the engine’s exhaust.
The motion is kept going by having a number of pistons connected together at different stages in the cycle. The straight-line piston motion becomes a rotation in the wheels. The internal energy of the engine is unchanged at the end of the cycle compared with that at the beginning. However, energy is lost to the surroundings and in the exhaust gases. So the energy supplied thermally by igniting the petrol equals the work done plus the thermal losses that heat the surroundings.

Entropy – a way of describing disorder
The second law is fundamental to what is happening to the Universe and to the direction of time, and is related to a measure of disorder called entropy.
Some events cannot go backwards in real life. They are events in which disorder sets in. For instance, a waiter drops a stack of plates and they shatter: you know that shattered plates cannot rise up and reassemble themselves in the waiter’s hands.
As the Universe develops, the ordering of its constituents gets less and less. The second law may also be expressed as:
Version 3 of the second law: It is not possible to have a process in which there is an overall decrease in the entropy of the Universe.
From our everyday experience, we know that some changes can occur and others cannot. We can understand why some events are so unlikely as to be impossible, by considering arrangements of molecules in a container. First, let us imagine a few molecules of a gas held in one half of the container by a partition. We then see what happens when we remove the partition. The molecules move around rapidly and very soon disperse throughout the container.
In the laboratory, we can demonstrate this effect with a coloured gas such as bromine. As they move around, the molecules will on average spend half their time on one side of the container, half the time on the other. What is obvious is the extreme unlikelihood of the molecules all simultaneously returning to the original side. Let us use some numbers to try and see why this is so. Suppose we start with 10 molecules only.
- When the molecules have had a chance to spread out, each molecule has a 50 per cent chance of being on the left side, that is, probability ½.
- For all the molecules to exist on the left-hand side there is a probability of: ½ × ½ × ½ × ½ × ½ × ½ × ½ × ½ × ½ × ½ or (½)10
This is 1 in 1024 – not a likely event, but one that can easily happen for a brief moment as the molecules speed around.
- But now suppose we increase the number of molecule to 1023 (less than the Avogadro number). We replace the 10 as used previously by 1023. The chance of all the molecules being on the left-hand side becomes:
(½)10ᶺ23 or 1 in 102422 or 1 in 1.7 × 1066 (To show that 102422 = 1.7 × 1066, use the xy key on your calculator.)
The likelihood of all the molecules being on the left side is therefore very small indeed:
- Suppose we want all the molecules to exist on the one side for a time t.
- For this to happen for total time t, there must be a time of 1.7 × 1066t when the molecules are dispersed on both sides.
- On average, we expect to wait for half of this time before a given situation occurs.
- So we can expect to have to wait for a time of the order of magnitude 1066t for the atoms to all be on the left side.
- So for all the molecules to exist on the left side for a time t of one microsecond we must wait (1066 × 10-6) seconds or approximately 1060 seconds. This is over 3 × 1052 years, which is many billions of times longer than the age of the Universe.
All this arises because there are approximately 1.7 × 1066 ways of arranging the molecules between the two sides of the container. For all of them to be on one particular side is one special arrangement.
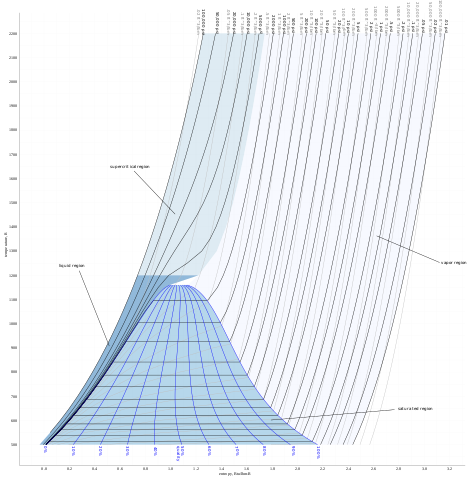
A temperature–entropy diagram for steam. Emok, CC BY-SA 3.0
The relation between entropy and number of arrangements
We say that entropy is a measure of the number of ways in which a system can exist. Whereas there is only one way of choosing all the molecules to be on one side, there are many ways in which we can select out half the molecules to exist in one half of the container, leaving the remainder in the other half. So a distribution with the molecules arranged either side of the barrier has a high entropy (lots of ways of choosing the molecules), and all molecules on one side has a low entropy (one way).
This was understood by Boltzmann, and the idea was developed much later by Planck. It became known as the Boltzmann-Planck hypothesis, expressed as:
S = k In W
Where W is the number of ways in which an arrangement can be set up (for instance an arrangement of molecules in a box), k is the Boltzmann constant and S is the value of the entropy measured in the same units as k (that is. JK-1).
As a system becomes more disordered, there is an increase in the number of ways its molecules or components can be arranged; The equation shows directly how the entropy increases. The equation eventually made an important contribution to quantum theory.
Life on Earth and entropy
At this point, you might wonder about the implications of entropy for biological life and its complexity. For instance, DNA is a very complex, ordered biological molecule, built from atoms and molecules that were arranged in a more random way. This seems to represent a reverse of the process of increasing entropy. Is it an example of overall negative entropy?
Certainly there is a local decrease in entropy as the arrangement of a biological molecule builds up. However, the entropy version of the second law makes it clear that there must be an overall increase in entropy of the molecule’s universe – its surroundings. So where exactly is the expected increase in entropy, an increase that should more than balance the local biological decrease?
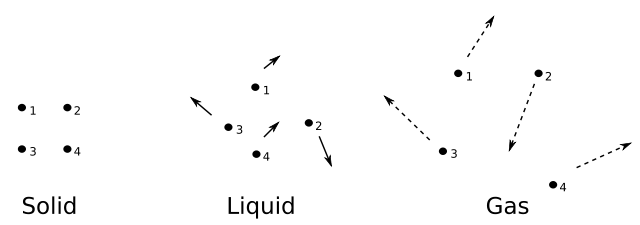
Solid-liquid-gas. Solid-liquid-gas.jpg: Sadi Carnot derivative work: Dave.Dunford, Public Domain
On the wide scale, a rapid increase in entropy is taking place in the Sun, the source of energy that sustains earth’s life. The Sun’s nuclear reactions produce huge amounts of thermal energy as random movements of particles and radiation. More locally, many biological processes involve a breakdown (reduction in complexity and order) in the material of their surroundings and, in so doing, give off thermal energy as a by-product.
It is rather as if the Sun and the Earth are acting as components of a heat engine (which will be discussed in the next post of mine). Just as in a heat engine, so, in life processes, energy is dissipated and the overall entropy of the surroundings is increased.
REFERENCES
https://opentextbc.ca/universityphysicsv2openstax/chapter/adiabatic-processes-for-an-ideal-gas/
Thermodynamics%2C_Electricity%2C_and_Magnetism_(OpenStax
https://www.grc.nasa.gov/WWW/k-12/airplane/thermo2.html
https://courses.lumenlearning.com/introchem/chapter/the-three-laws-of-thermodynamics/
https://www.livescience.com/50941-second-law-thermodynamics.html
https://en.wikipedia.org/wiki/Second_law_of_thermodynamics
https://en.wikipedia.org/wiki/Engine
https://en.wikipedia.org/wiki/Internal_combustion_engine
https://www.britannica.com/science/entropy-physics
https://en.wikipedia.org/wiki/Entropy
https://en.wikipedia.org/wiki/Entropy_(order_and_disorder)
https://lavelle.chem.ucla.edu/forum/viewtopic.php?t=18145
https://opentextbc.ca/introductorychemistry/chapter/entropy-and-the-second-law-of-thermodynamics-2/
http://www.digital-recordings.com/publ/publife.html
That is a good post (I almost ended up teaching this next year). Thanks for putting it up together.
Can I maybe ask you to do something for the large amount of white spaces in the reference list? This make the post look weird, at least on steemstem.io. Thanks in advance!
Yes, thanks Prof. I've fixed the large amount of white spaces. I don't know what caused it in the first place.
Cool thank you! :)
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.