Solar cell efficiency and the solar spectrum: why only 33%?

This post is intended both as a brief explanation of some of the physics behind solar cell conversion efficiency, and as a resource for anyone looking for further information on solar cell modelling and efficiency calculations. It relates to some of my work as an academic photovoltaics researcher, and hopefully it will be both interesting and understandable.

Firstly, what is a solar cell and why does their efficiency matter? A solar cell or photovoltaic device is a direct energy conversion device which converts light into electricity. They are a key renewable energy technology, and because of the incredible abundance of energy in sunlight – more energy hits the Earth in an hour than the whole of our species uses in an entire year – they have the potential to generate most if not all of the energy required by humanity. Most solar cells are solid-state semiconductor devices and operate using the same basic physics as the CPU in your computer. Current commercially available devices have a typical energy conversion efficiency of 20-25%. This may not sound particularly great but is actually reasonably comparable with other generation technologies, both renewable and otherwise. Of course the greater their efficiency the more electricity we can generate!

Evening light through the trees outside the lab where I work

A brief introduction to the solar spectrum

The extraterrestrial solar spectrum can be approximated reasonably well by a Planck blackbody spectrum for a blackbody at a temperature of around 5800 Kelvin. The Earth’s atmosphere attenuates that spectrum in various ways, with the result that the light we actually see is a little different. If the proportions of the various components of the atmosphere are known, then along with time and location data these values can be used to calculate the spectrum at the Earth’s surface. There are many programs that can be used for this, but the one used most often by the photovoltaics research community is known as SMARTS, and is available through the US National Renewable Energy Laboratory website (https://www.nrel.gov/rredc/smarts/). The standard spectrum used in solar cell efficiency measurements and calculations is known as AM1.5G.

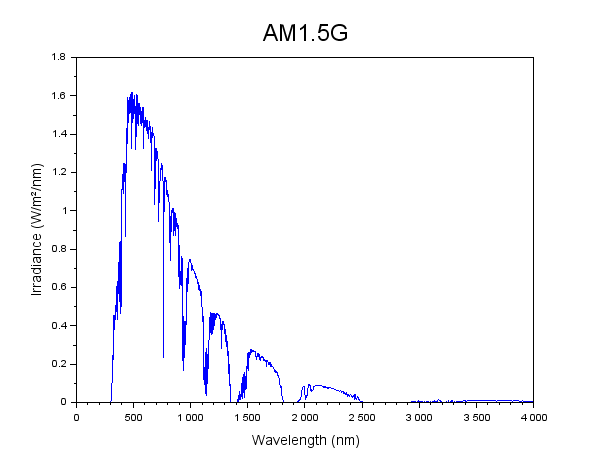
AM1.5G solar spectrum calculated using SMARTS. AM stands for air mass, and is a measure of the relative thickness of atmosphere the sunlight has had to travel through in order to reach the Earth’s surface. An air mass of 1.5 corresponds to a zenith angle of roughly 40 degrees. G stands for global, meaning that the spectrum also takes into account diffuse light caused by atmospheric scattering effects.

Solar cell efficiency: numerical and analytical approaches

Solar cell efficiency was first examined systematically by William Shockley and Hans Queisser, who published a seminal paper on their calculations and findings in 1961 [1]. As a consequence, the maximum efficiency limit for solar cells is often called the Shockley-Queisser limit. Their calculation, which they referred to as the detailed balance limit, is a numerical approach and uses a series of theoretically reasonable but practically implausible assumptions, most notably that the cell is both optically and electrically perfect. Consequently the Shockley-Queisser limit is an absolute upper efficiency limit, and should not be considered a guideline as to what is practically achievable! In their calculations, Shockley and Queisser also assumed a Planck blackbody spectrum which as I described earlier is only a reasonable approximation of sunlight if you are in space. Luckily it is quite straightforward to adjust their calculations to use any input spectrum, and so the Shockley-Queisser limit can be calculated for ground-level spectra such as AM1.5G. The maximum achievable efficiency for a single cell is about 33.7%.

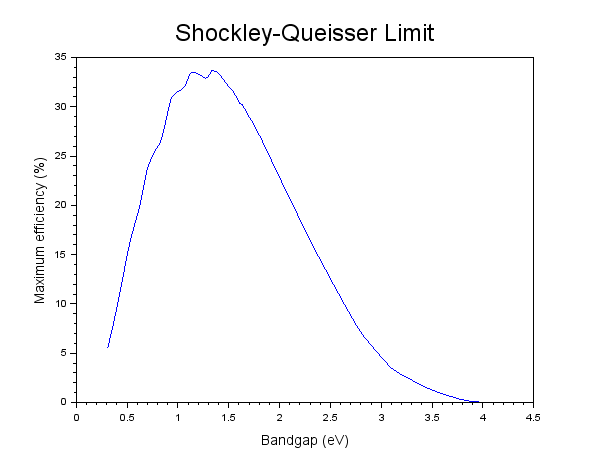
Shockley-Queisser limit for AM1.5G spectrum

Whilst the Shockley-Queisser calculations give a useful indication of maximum efficiencies for cells with different band gaps (the semiconductor material property which determines which part of the spectrum the cell usefully absorbs), the one thing they do not provide is any significant quantification of the causes of energy loss. An alternative approach was developed more recently which uses an analytical technique, deriving cell efficiency and associated losses from thermodynamic first principles [2]. The disadvantage to this approach is that it can only be used for a blackbody spectrum.

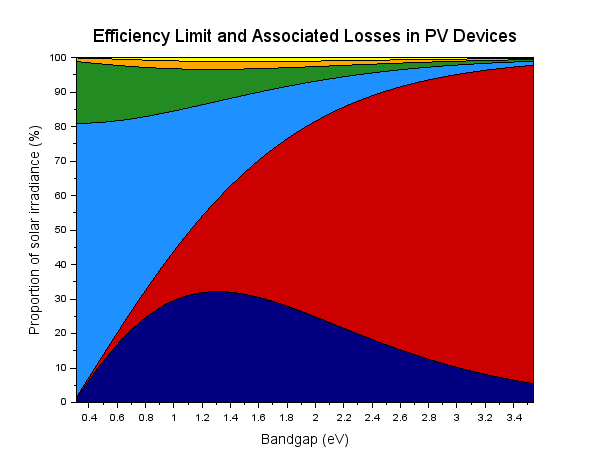
Theoretical efficiency limit and associated losses. The dark blue curve represents power output; red, below band gap transmission losses; pale blue, photon cooling or thermalisation losses; green, Boltzmann or étendue expansion losses; orange, Carnot losses; and yellow, radiative recombination emission losses.

The main benefit of identifying the loss mechanisms is that it enables investigation of techniques for reducing these losses. A bewildering array of different possibilities have been suggested over the years, but there is one which is known to work and has been demonstrated quite effectively. This is known as solar concentration, and involves putting a cell under some sort of lens or focussing mirror system. This increases the efficiency of the cell through reduction of the Boltzmann or étendue expansion loss. Etendue expansion losses are a result of the disparity in the solid angle between the sun as seen by the cell and that of the cell itself. Solid angle is in effect a measure of how big an object looks from a given location. Despite its actual size, the sun looks very small when seen from the cell; hence its solid angle is very small (~6.8E-5 steradians). The cell’s solid angle at the same point is very large (π steradians). By either increasing the sun’s solid angle or decreasing that of the cell, this loss can be reduced and in theory eliminated. Using a lens or mirror system increases the apparent size of the sun, hence the solar solid angle is increased. Using this technique to completely eliminate étendue expansion losses is probably not really achievable in reality however as it would require magnifying the incident sunlight by about 42,600 times!

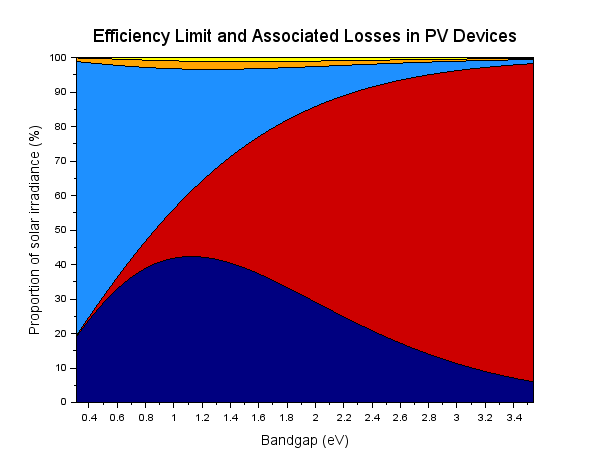
Theoretical efficiency limit and associated losses under maximum concentration. Colours are as for the previous figure; however étendue expansion losses are no longer present due to matching of the spectral and cell emission solid angles.

Finally, a note of caution regarding efficiency and its effect on cost. On the face of it, maximising efficiency seems like the best approach as it means that the maximum amount of energy can be squeezed out of the incident sunlight. In practice however increasing efficiency beyond a certain point typically becomes economically costly. This is one reason why there are relatively few photovoltaic concentrator systems in use despite their increased cell efficiencies. The key metric is actually cost-effectiveness. Efficiency is absolutely an important part of that, but it is not the only thing to consider!

For further reading, Wikipedia is a good starting point:

https://en.wikipedia.org/wiki/Photovoltaics
https://en.wikipedia.org/wiki/Shockley%E2%80%93Queisser_limit
https://en.wikipedia.org/wiki/Etendue

Also PVEducation:

http://www.pveducation.org/pvcdrom/instructions

For other resources including spectra, PV Lighthouse is very useful:

https://www.pvlighthouse.com.au/

Finally, the figures in this article were generated using two Scilab scripts. Scilab (http://www.scilab.org/) is a free open-source programming environment similar to Matlab. My two scripts and associated documentation can be found at:

https://github.com/ElPatito/PV-efficiency-calcs

References:

[1] Shockley, W., Queisser, H. J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J Appl Phys 32, 510, 1961. DOI:10.1063/1.1736034

[2] Hirst, L. C., Ekins-Daukes, N. J. Fundamental losses in solar cells. Progress in Photovoltaics 19, 3, 286-293, 2011. DOI: 10.1002/pip.1024