DE PITÁGORAS A EUCLIDES O DE CÓMO SE PUEDE TRANSFORMAR SIN TRAICIONAR
Un gran agujero fue lo que dejó el pitagorismo a la posteridad con el problema de los inconmensurables. En el fondo, los de la caverna esperaban que todo pudiera medirse con números enteros, independientemente de la referencia que se buscara. Por ejemplo, para los dos segmentos de la figura siguiente

puede conseguirse un segmento menor a ambos que cabe 5 veces exactas en el más pequeño y 11 en el mayor.
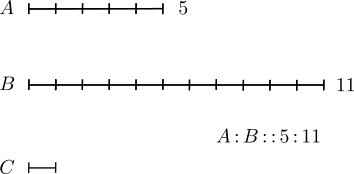
Si decimos que el segmento menor se llama A y el mayor B, entonces el segmento diminuto C mide a ambos, A y B, un número entero de veces y la relación se expresa diciendo que A es a B como 5 es a 11, frase que mucho tiempo después se simbolizaría como A:B::5:11. A una relación como ésta los griegos la llamaron analogía y nosotros tradujimos el término como proporción. Durante un buen tiempo, apegados a su consigna Todo es número, los pitagóricos estaban seguros de que, dados dos segmentos (mejor aun: dos magnitudes) cualesquiera el segmento (o magnitud) diminuto que las medía a ambos en forma entera, aparecería siempre; en otras palabras: que la proporción terminaría invariablemente en un par de números (como 5 y 11, por ejemplo). Pero esa esperanza sería cruelmente fulminada por dos de las figuras más queridas por la hermandad: el cuadrado y el pentágono regular:
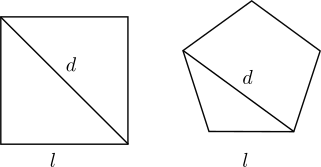
pues sus diagonales se resistían a medirse en forma entera con sus lados respectivos.
El golpe teórico fue desolador (aunque D. Fowler no está de acuerdo con esta visión pesimista), pero los intrusos fueron admitidos y catalogados. Se les llamó magnitudes inconmensurables y se intentó -sin éxito- conseguir una definición para ellas, que no apareció sino dos siglos después de la mano de un discípulo brillante de Platón: Eudoxo de Cnido. A pesar de esta carencia de definición, los pitagóricos -en una muestra de optimismo desbordante- se animaron a usar lo inconmensurable para demostrar algunas proposiciones geométricas, entre las cuales destaca el teorema que hizo más famoso al maestro, al punto que su nombre lo lleva como marca indeleble: el teorema de Pitágoras:
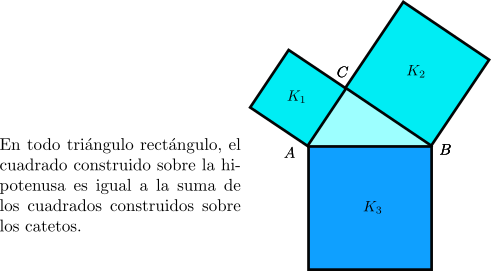
Aludiendo a la figura, el teorema dice que K1+K2=K3, si el triángulo ABC es rectángulo con su ángulo recto en C. Esta suma no debe entenderse en el sentido algebraico con el que la interpretamos hoy, pues los griegos carecían de notación algebraica y del concepto de número real. Una de las traducciones españolas más conocidas de los Elementos de Euclides (María Luisa Puertas Castaño), traduce el enunciado del teorema de Pitágoras (proposición 47 del primer libro) de la siguiente manera:
En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto.
En realidad es una proposición absolutamente geométrica que habla de identificación de figuras geométricas. No puedo entrar en más detalles, volvamos a los inconmensurables.
Empiezo por decir que lo que hay al respecto son puras conjeturas históricas; recordemos que el pitagorismo original no dejó obra escrita, pero por muchas razones los historiadores sospechan que la demostración del pitagorismo (si es que la hubo) siguió las líneas de la siguiente ilustración:
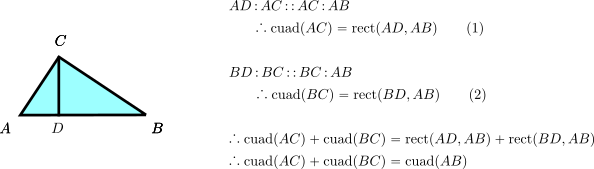
en la que las proporciones se establecen por la semejanza de los tres triángulos rectángulos que se pueden identificar al bajar la altura desde el vértice del ángulo recto. Obsérvese que la primera proporción dice que el segmento AC es media proporcional entre los segmentos AD y AB; geométricamente esto significa (era una demostración temprana para ellos) que el cuadrado construído sobre el segmento AC es igual al rectángulo construído con los segmentos AD y AB. Un razonamiento idéntico permite decir lo mismo de los segmentos BC, BD y AB. Podemos hacer una ilustración gráfica:

en la que se ve claramente que ambos rectángulos componen el cuadrado sobre la hipotenusa.
A nuestros ojos la demostración es impecable; a los de los pitagóricos, no. Se usan proporciones entre segmentos, esas proporciones podrían contener segmentos inconmensurables y el pitagorismo quedó en mora con esta definición. Lógicamente, hay un vacío.
Nos movemos entonces tres siglos adelante para revisar los Elementos de Euclides, obra magna de la ciencia del periodo alejandrino, en la que -cónicas aparte- se recoge todo el saber matemático de la época. En los Elementos conseguimos el teorema de Pitágoras y también la solución de Eudoxo al problema de los inconmensurables. Pero Euclides necesitó el teorema del triángulo rectángulo muy temprano, de hecho, el primer libro se cierra con el teorema y su recíproco. Los inconmensurables esperarían hasta el quinto libro.
¿Qué demostración usó Euclides entonces para el teorema del triángulo rectángulo? Pues... la misma demostración pitagórica, solo que con un toque mágico que permitió evadir a los inconmensurables: para cada cuadrado de los catetos dibujó dos líneas auxiliares, que hacían aparecer dos triángulos congruentes por el criterio LAL (Lado-Ángulo-Lado), tal como se ve en la figura que sigue.
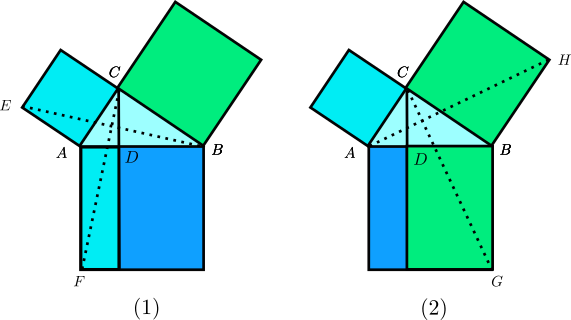
A la izquierda, los triángulos congruentes son EAB y CAF, el primero de los cuales comparte base y altura con el cuadrado sobre el cateto AC y el segundo comparte base y altura con el rectángulo de diagonal DF. Es decir: los triángulos son la mitad de los cuadriláteros correspondientes y, por tanto, ellos son iguales (en área). A la derecha, los triángulos auxiliares son ABH y CBG, lo que da igualdad (de áreas) entre el cuadrado sobre el cateto BC y el rectángulo de diagonal DG. La unión de los rectángulos da el cuadrado sobre la hipotenusa AB.
¡Maravilloso! Se mantiene la idea, pero sostenida sobre un terreno lógico absolutamente sólido. El historiador Proclo elogia este golpe de timón con las siguientes palabras [Ref. 4. Pág. 337. La traducción es mía.]:
Si prestamos atencion a quienes gustan de contar cosas antiguas, encontraremos que atribuyen este teorema a Pitágoras y añaden que sacrificó un buey por su descubrimiento. En lo que a mı́ concierne, aunque me asombran quienes primero notaron la verdad de este teorema, admiro aún más al autor de los Elementos, no solo por la prueba lúcida y eficiente que de él da, sino tambien porque en el sexto libro presenta un teorema aún más general que éste y lo fundamenta sobre argumentos cientı́ficos irrefutables. En efecto, en ese libro demuestra, de manera general, que en los triángulos rectángulos la figura sobre el lado que subtiende el ángulo recto es igual a las figuras semejantes (trazadas de manera similar) sobre los lados que contienen el ángulo recto.
El texto de Proclo contiene varias cosas interesantes:
- El historiador no está seguro de que el teorema sea de Pitágoras: a él le llegó de oídas la información.
- La prueba de Euclides le parece la más "lúcida y eficiente" de todas las que conoce.
- Hace notar que el teorema es un caso particular de otro del propio Euclides, que aparece en el libro sexto (se trata de la proposición 31). Sin embargo, incluso esta generalización euclidiana se puede llevar aun más lejos, si consideramos un triángulo rectángulo cualquiera, sobre cuyos lados construimos a escala tres figuras semejantes (homotéticas, para ser más precisos). Si las figuras sobre los catetos se denominan F1, F2 y la de la hipotenusa es F3, entonces F1+F2=F3, tal como se muestra en la ilustración que sigue:
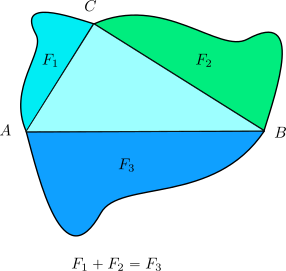
La demostración en este caso tan general exige herramientas que van bastante más allá de la geometría de los Elementos.
Para finalizar, los voy a dejar con la traducción al español (M. L. Puertas Castaño) de la demostración que aparece en los Elementos. Espero que la disfruten.
En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto.
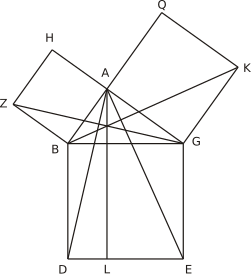
Sea ABG el triángulo rectángulo que tiene el ángulo recto BAG.
Digo que el cuadrado de BG es igual a los cuadrados de BA, AG.
Trácese pues a partir de BG el cuadrado BDEG, y a partir de BA, AG los cuadrados HB, QG, y por el (punto) A trácese AL paralela a una de las dos (rectas) BD, GE; y trácense AD, ZG. Y dado que cada uno de los ángulos BAG, BAH es recto, entonces en una recta cualquiera BA y por un punto de ella, A, las dos rectas AG, AH, no colocadas en el mismo lado, hacen los ángulos adyacentes iguales a dos rectos; por tanto, GA está en línea recta con AH. Por la misma razón, BA también está en línea recta con AQ. Y como el ángulo DBG es igual al (ángulo) ZBA --porque cada uno (de ellos) es recto-- añádase a ambos el (ángulo) ABG; entonces el (ángulo) entero DBA es igual al (ángulo) entero ZBG; y como DB es igual a BG, y ZB a BA, los dos (lados) DB, BA son iguales respectivamente a los dos (lados) ZB, BG; y el ángulo DBA es igual al ángulo ZBG; entonces la base AD es igual a la base ZG, y el triángulo ABD es igual al triángulo ZBG; y el paralelogramo BL es el doble del triángulo ABD: porque tienen la misma base BD y están entre las mismas paralelas BD, AL; pero el cuadrado HB es el doble del triángulo ZBG: porque tienen a su vez la misma base ZB y están entre las mismas paralelas ZB, HG; [pero los dobles de cosas iguales son iguales entre sí]; por tanto, el paralelogramo BL es también igual al cuadrado HB. De manera semejante, trazando las (rectas) AE, BK se demostraría que también el paralelogramo GL es igual al cuadrado QG; por tanto, el cuadrado entero BDEG es igual a los cuadrados HB, QG. Asimismo, el cuadrado BDEG ha sido trazado a partir de BG, y los (cuadrados) HB, QG a partir de BA, AG. Por tanto, el cuadrado del lado BG es igual a los cuadrados de los lados BA, AG.
Por consiguiente, en los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de ·los lados que comprenden el ángulo recto. Q. E. D.
NOTA ACLARATORIA: Todas las imágenes del post fueron elaboradas por mí, con el programa Inkscape, el cual es software libre.
REFERENCIAS
Euclides. Elementos. Traducción y notas de Marı́a Luisa Puertas Castaños. Edit. Gredos, Madrid, 1991. (Tres volúmenes).
David Fowler. The Mathematics of Plato’s Academy. Clarendon Press, Oxford, 1999.
Douglas Jiménez. Historia de la matemática: Pitágoras y el pitagorismo. CreateSpace.com. 2013.
Proclus. A commentary on the first book of Euclid Elements. Translated with Introduction and notes, by Glenn R. Morrow. Princeton University Press. New Jersey, 1970.
Fabuloso post, @dougjim. He refrescado y aprendido varias cosillas con él. Sabía eso que mencionas de Pitágoras, que él mismo no dejó obras escritas y que el teorema que lleva su nombre ya era conocido por otras culturas. Admirable el trabajo de Euclides por como nos lo presentas aquí, y todavía más las demostraciones más generales que le sucedieron y que seguro seguirán apareciendo. Éxitos.
Gracias, @eniolw. Me alegra que te haya gustado. La divulgación matemática es mi tema desde hace bastantes años. Continuaré con ella. Puedes mirar algunos de mis posts anteriores, como también revisar mi otro blog. Igualmente te invito a leer los que vendrán en el futuro.
Congratulations @dougjim! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Thank you very much, @steemitboard.
Hola @dougjim, me gustó mucho tu trabajo, no solo cuenta con las precisiones matemáticas e históricas relativas al tema sino que le has logrado imprimir al escrito un tono de aventura que lo hace encantador, estoy fascinada por tu narrativa lo cual para ser un post de Matemática representa un agradable valor agregado, serías un artista entre la comunidad estudiantil de esta área científica en particular si escribes cómics de Matemática con el estilo de esta publicación, tendrías muchos fans e impulsarías en grado sumo el estudio de la Matemática en la población juvenil!! Saludos cordiales!!
Gracias @reinaseq por tu entusiasmo y generosidad. Tus propuestas son muy interesantes.
Gracias, @ramonycajal.
Congratulations @dougjim! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Thank you very much for your support, @steemitboard.
ME GUSTO
SALUTATIONS DU VENEZUELA
Greetings from Venezuela
Gracias, @soy-venezuelien.
This post has been voted on by the SteemSTEM curation team and voting trail.
If you appreciate the work we are doing then consider voting us for witness by selecting stem.witness!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thank you very much, @steemstem for your support.