Giving life to Ordinary Differential equations
As every engineer or engineering student knows, almost everything in the world can be translated into numbers, this is especially helpful with physical problems, because using several tools that math gives us, we can find solutions that can be reflected in the real life later, and thus the problems are solved. These tools come from knowing in extend some branches of math like, algebra, geometry, trigonometry, calculus, etc.
In this post I´ll talk about a very useful aspect of calculus and it´s applications, the Ordinary Differential Equations (ODE) of first order, which are expressions where the unknown variable is a function, and include only the first derivative of said function (Thus of first order). Of course, there are ODEs of second or even higher orders (where the second, third or so on derivatives can be present in the equation) and Partial differential equations (PDE) that depend on several variables, but those are a topics a bit more complex.
 Isaac Newton, Father of the Differential calculus by Sir Godfrey Kneller
Isaac Newton, Father of the Differential calculus by Sir Godfrey Kneller
First we have to understand the concept of Modeling in engineering, this is when we take a problem and we give it a numerical representation, this is known as mathematical model, once we have the model ready, we proceed to find a mathematical solution, and later we give the solution a physical interpretation. Most programs and calculators can give you a help in finding a numerical answer, but the trick is in creating the mathematical model, and bringing the answer to real life.
To fully understand the equations and principles that I’ll discuss here, you´ll need some basic knowledge of Integral calculus, more specifically an understanding of derivatives (their real world, or physical applications) and some methods of integration.
A First-order ODE can be written in an explicit form like this
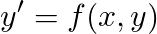
A general solution for this is any function i.e. g(x) that on some open interval a < x < b is defined and differentiable in that interval, and is such that replacing g and g’ in y and y’ the equations becomes an identity.
There are some ODEs that can be reduced to with common algebra to this form
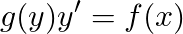
Where we can further develop and integrate each side, because in calculus y’ = dy/dx
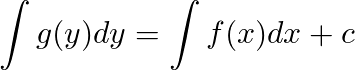
We should note that each integral throws a different constant “c”, one in the right and another in the left side of the equation, but these constants can be considered together as one. This method is called separating variables, because the variables are in different sides, “y” only appear at the left side, and “x” in the right.
Let´s do an example of this method with the following ODE, we´ll find a general solution
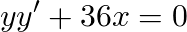
First we transform y’ into dy/dx, and then we separate both variables.
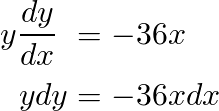
Now, we integrate both sides
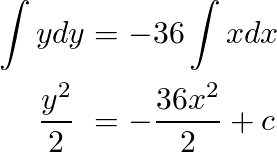
Rearranging the formula, we can see that it belongs to a large array of ellipses, which vary with the constant “c”
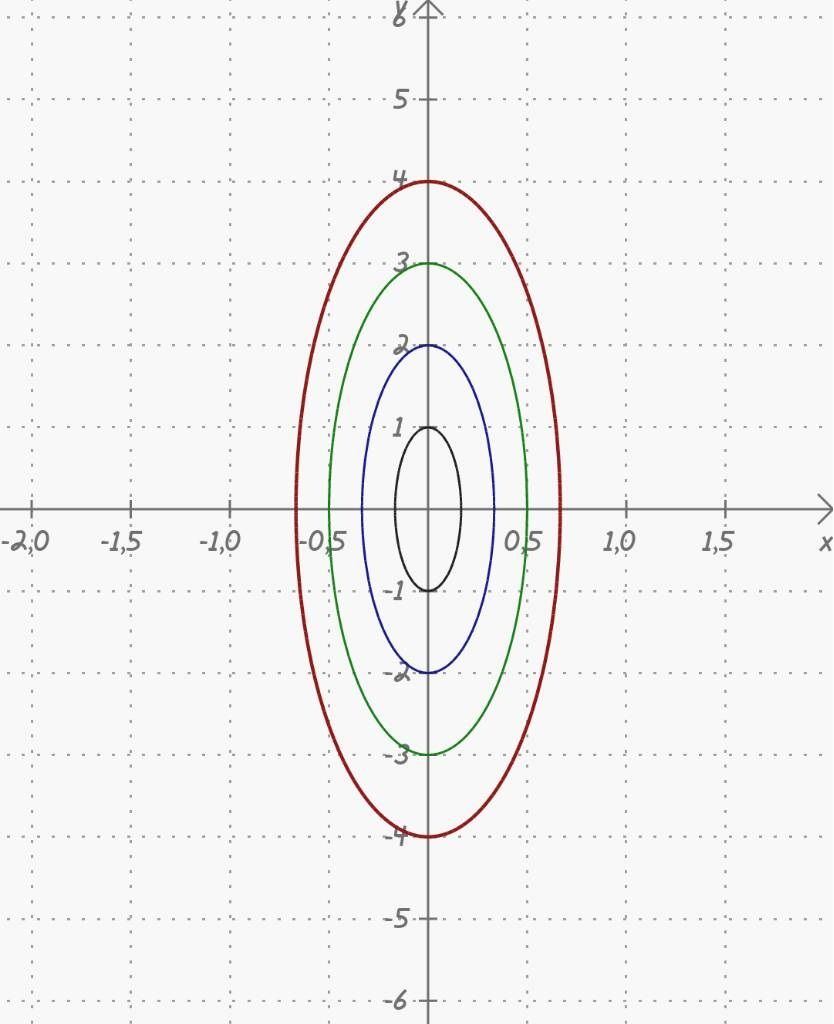
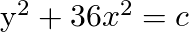
Given this powerful method for finding solutions to first-order ODE we can continue into the real deal, the applications of these equations.
Radioactive Decay
Experiments show that at each instant a radioactive substance decomposes—and is thus decaying in time—proportional to the amount of substance present.
If we chose to represent y(t) as the amount of substance present at any time “t” of a radioactive element. We know by physical law that the time rate change is represented by y’=dy/dt.
Giving the stated (by experiments) proportionality, we define the next first order ODE
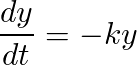
This is because in math, proportionality between two magnitudes is represented by a constant “k” giving it a minus in the formula, we´ll get the decaying implied. The value of "k" is found with experiments of the radioactive substance of interest.
Applying the method of separating variables we get easily the general solution of the ODE
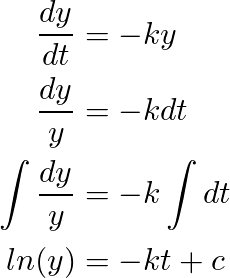
By properties of the natural logarithm and “e” constant
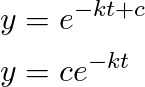
Where “c” is the initial amount of the radioactive substance of interest, say “y0” the other constant “k” should have a compatible unit with “t”
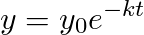
Given 0,9 g of 232U, find the amount present at any later time, given that it´s constant "k" is 1x10-2 years-1
We start with the formula of Radioactive decay, and then we substitute our initial values to find the answer with relative ease
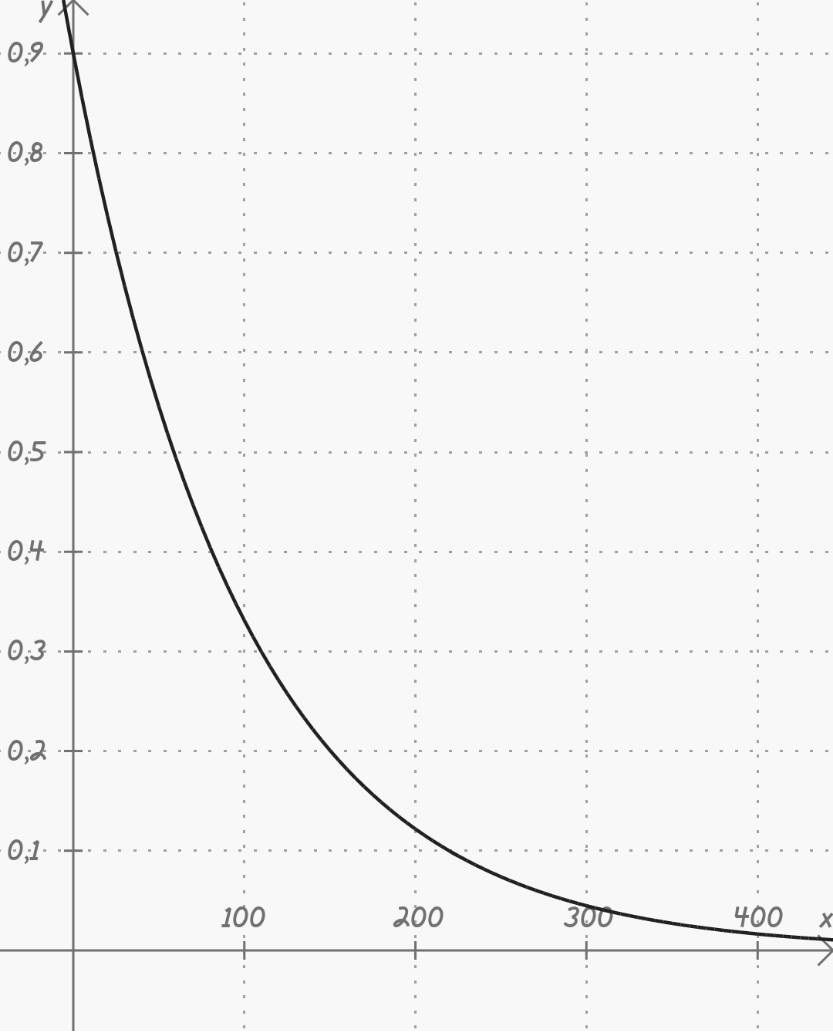
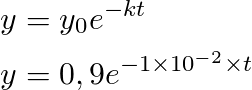
This formula will give us any amount of 232U in grams when introducing a time in years given the initial amount of 0,9 g. For example, in a hundred years there will be
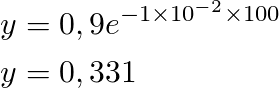
Radiocarbon Dating
This is a specific case of study that derives from Radioactive decay, there is radioactive carbon 14C in the atmosphere, and it gets into the blood stream of any living being by breathing and eating, but when the organism dies, this absorption halts, effectively stopping the gathering of new 14C molecules in the body. The isotope 14C decays into 12C, so by measuring the rate of 14C/12C in a relic, we can determine the age of said remain.
For example, we´ll suppose there is a relic with a rate of 14C/12C = 58 %, and we need to know how old it is, for this we are given the half-life of 14C, which is 5715 years
Taking the equation that we found in Radioactive Decaying we start with
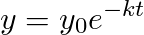
Half-life is a measure of time, which says the amount of time needed to decompose a certain quantity of a radioactive element to the half, having the half-life (H = 5715) for 14C we can found “k” by simply taking “H” as “t” and “y” as y0/2
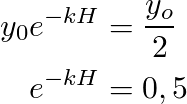
By properties of the natural logarithm and e constant
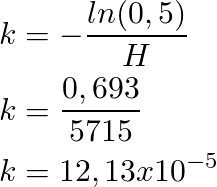
Now, we use the ratio of carbon 14C - 12C = y/ y0 = 58 %
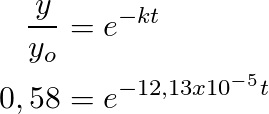
Some more logarithm properties and we get the result in years
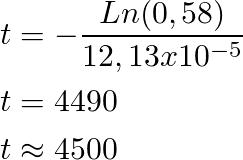
Mixing Problem
We can apply ODE of first grade to solve a mathematical model of a mixing tank. This is something very common in the chemical industry.
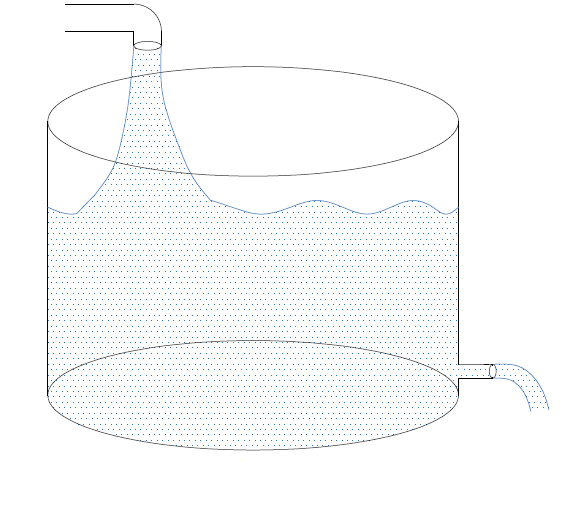
For this example, we have a tank that contains 3800 litres of water, were 45 kg of salt were deluded initially (we won´t take into consideration the volume of salt). Brine gets into the tank through a pipe at an estimated rate of 38 litres/min, and each litre has 0,5 Kg of salt in it. Brine also runs out from another pipe at 38 litres/min. Find the amount of salt in the tank at any time "t"
Assuming y(t) as the amount of salt in the tank at a time “t”. The rate of change will be
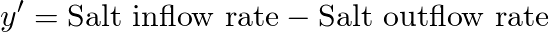
With 0,5 Kg of salt times 38 litres we have 19 Kg of salt entering the tank, while the outflow is 38 litres of brine, this represents 38/3800 = 0.01 (1 %) of the total volume of the tank, that is 0,01 of the salt in the tank at any time y(t), so the outflow can be written as 0,01y, and the ODE for this problem is
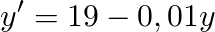
Let´s use the separating variable method now
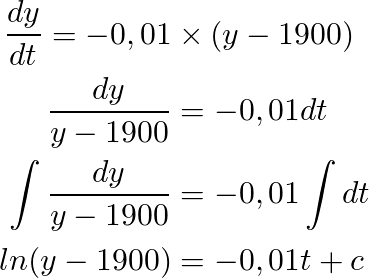
As always, using properties of the natural logarithm and e constant
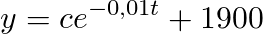
Now we take our initial values, with t0 there are 45 kg of salt in the thank, so
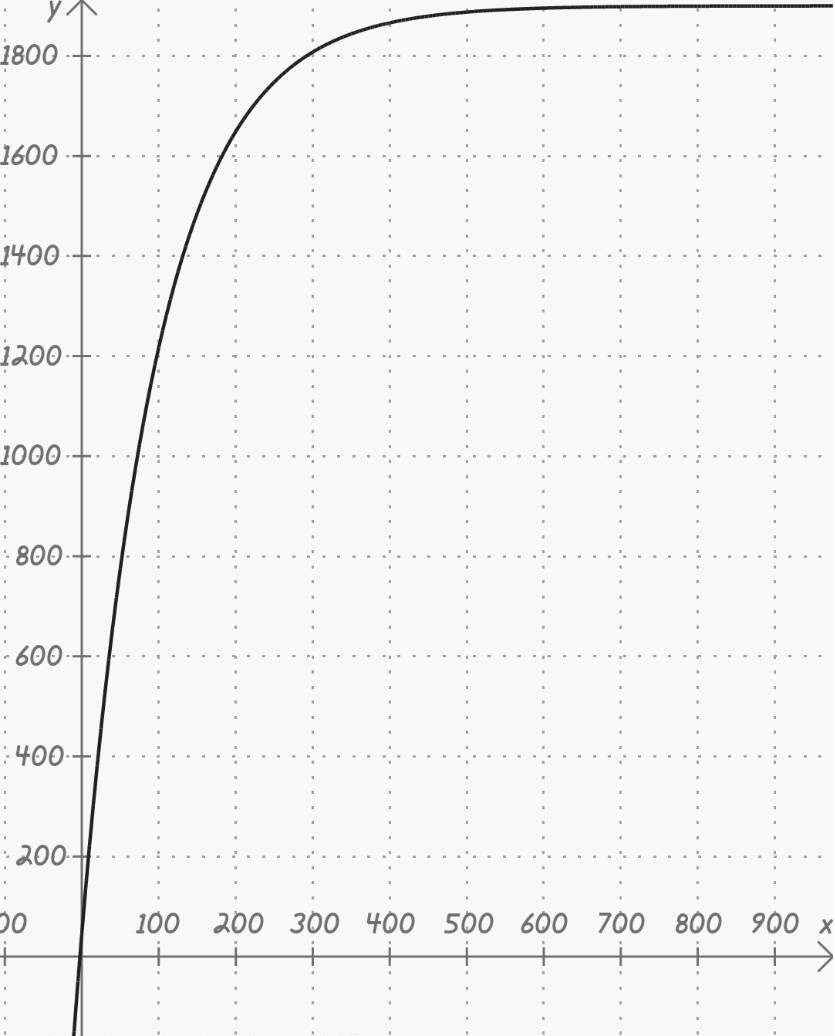
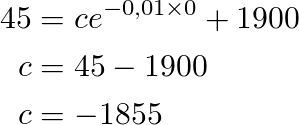
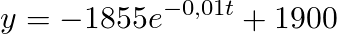
This equation will grant us the amount of salt in the tank (in kg) in any given moment, by just using it with the time in minutes.
Newton’s law of cooling
Parting with the assumption that the time rate of change of the temperature of a body (T for the temperature) that conducts heat well, like copper, is proportional to the difference of the temperature of the body and the surrounding medium, we can go on with the next application of ODEs, referred as Newton´s law of cooling.
In our next example we have an office room with an air conditioner set to 16 °C, the office (and thus the AC also) works from 6 a.m. to 8 p.m. In summer the temperature around the office reached 30 °C (We will assume it stayed like this the whole day, because it´s simpler to model) and in a given day at 1 a.m. the temperature of the building was found to be 23°C, What was the temperature of the office at opening time (6 p.m.)?
Let T(t) be the temperature inside the building and 30 the outside temperature “TA” (assumed to be constant in Newton’s law). Then by Newton’s law
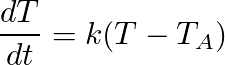
Applying the method of separating variables and logarithm properties
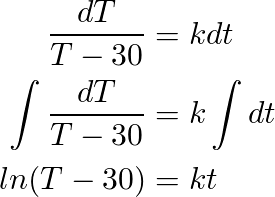
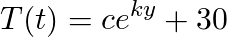
Taking “t0” as 6 p.m. we assume the temperature in the building at the end of day is the one the AC was set to function, so T(t0) = 16 °C
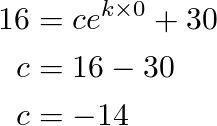
With the other data “at 1 a.m. the temperature of the building was found to be 23°C” we can assume that T(t7) = 23 °C
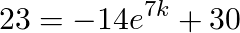
By properties of the natural logarithm and e constant
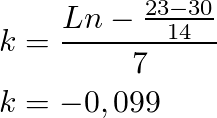
Finally with our fully defined solution we can find the value of T(t10) (the temperature at 6 a.m.)
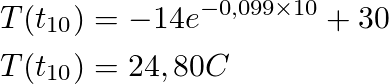
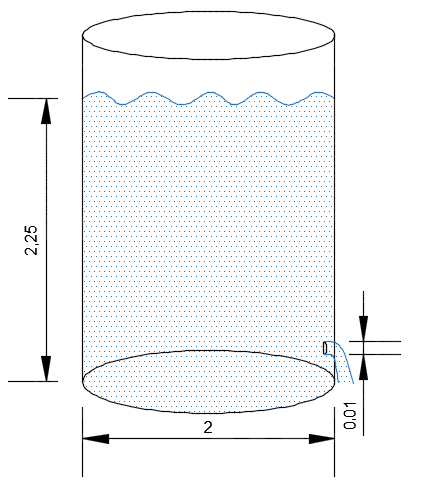
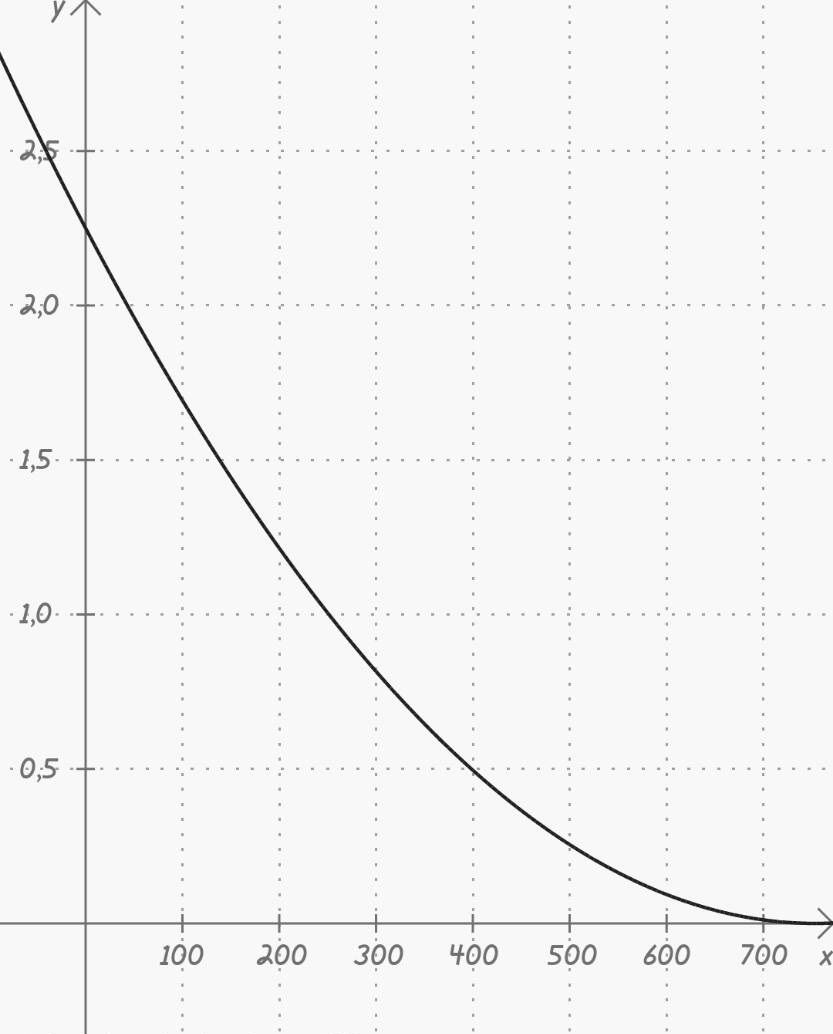
Leaking Tank (Torricelli’s Law)
Maybe we want to find the height of water in a tank at any time (t), Knowing that the tank has a 2 m diameter, a hole with a diameter of 1 cm, and the initial height of the water when the hole was drilled was 2,25 m. Of course this problem can be solved with our current understanding of ODEs, first of we apply the Torricelli’s Law, that law says that under the influence of gravity the velocity of outflowing water can be modeled as
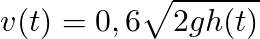
Where “g” is the acceleration of gravity = 9,81 m/s2 = 35316 m/min2 for this example. Outflowing volume and its variation can be expressed as the Area of the hole (A) multiplied by the velocity “v” during a variation of time “t”
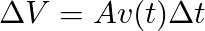
Similarly, the variation of volume in the tank can be modeled as the Area of the tank multiplied by the change in height “h”
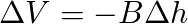
Equating both formulas of ∆V
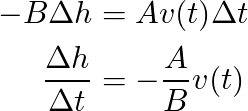
Let´s make the interval of study ∆ approach to a value of 0 so we can get the ODE of this model; this technique is standard in ODE modeling to obtain derivatives.
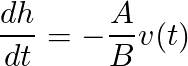
Substituting the Torricelli’s Law in the last expression
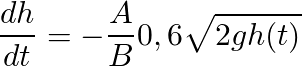
We can now begin to separate the variables and find the solution to the ODE, but first we should note that the square root of 2g times 0,6 equals to 159,46
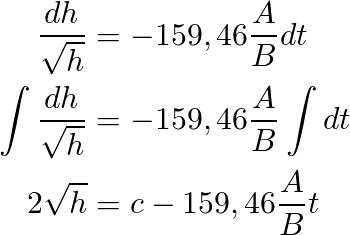
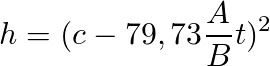
For our problem we have that
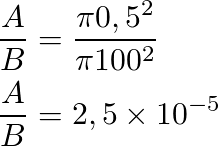
Substituting in the former formula we get
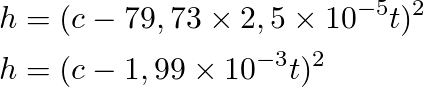
With the initial value of h(t0) = 2,25 m or 225 cm we find “c”
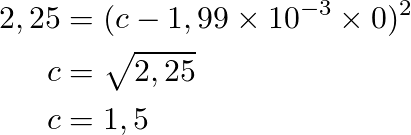
And the solution is
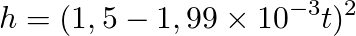
About making this post
I wanted to make this post because I find the ODEs fascinating, as everything we use in our efforts to make reason out of the nature.I learned everything here thanks to the Tenth Edition of ''Advanced Engineering Mathematics'' by Erwin Kreyzig, which is an amazing book, the examples were picked, adapted and given another explanation with the help of QuickLatex for the formulas, AutoCAD for the drawings and the mobile version of Mathlab graphic calculator for the graphics. I truly hope you enjoyed this post as much as I did making it.
Hola @count-antonio, upv0t3
Este es un servicio gratuito para nuevos usuarios de steemit, para apoyarlos y motivarlos a seguir generando contenido de valor para la comunidad.
<3 Este es un corazón, o un helado, tu eliges .
: )
N0. R4ND0M:
9825 6903 4321 1466
6469 3586 3184 2129
2487 9361 2834 3580
5805 8278 8097 8917
Congratulations @count-antonio! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP