Numbers, We use them but we know what they are?
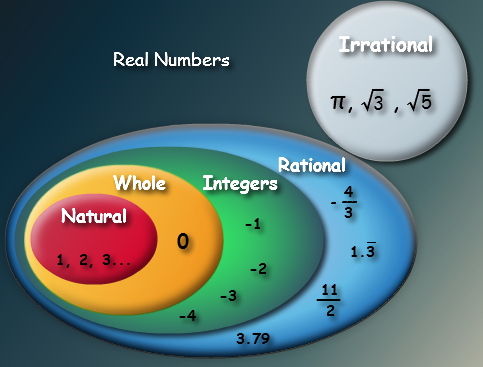
From Latin numĕrus, the term number refers to the expression of a quantity in relation to its unit. It is, therefore, a sign or a set of signs. One (1), two (2), three (3), four (4), five (5), six (6), seven (7), eight (8), nine (9) and zero (0) are the natural numbers. In any case, it should be noted that some mathematicians do not consider zero among natural numbers.

Source
The set of integers is made up of natural numbers and negative numbers (-1, -2, -3, etc.). Number theory recognizes other classifications, such as prime numbers (the natural number that has only two divisors: itself and the one) and rational numbers (which can be represented as the quotient of two integers that have a non-zero denominator).
Source
In addition to all this, we find another wide variety of numbers. Thus, we can also refer to those known as Roman numerals which are those that give shape to the numbering system created during Ancient Rome and which are concretely capitalized letters representing the different quantities.
In this way, for example, V equals number 5, L corresponds to 50, D has a value of 500, M is equal to 1000 and X corresponds to 10.
Source
In the same way, we can not ignore the existence of those known as ordinal numbers, which are those used to establish a well-ordered set, to give an order to a specific sequence. In this way, we would have: first, second, third, fourth ...
Opposite these last ones are those known as cardinal numbers, which are basically used for counting. Among them are 1, 2, 3, 4 ...
In addition to all these mentioned numbers, we can also speak of the Arabic numbers, which are those that belong to the Arabic numeral system, or of the fractioned numbers that are those that we identify as broken. An example of the latter case would be 2/3.
To all this, we would have to add the fact that there are a series of numbers that are considered to have mysteries enclosed or that are related to a very specific element. In this way, for example, 666 is associated with Satan, as is evident in the New Testament Apocalypse.
On the other hand, a number of people or things is known as a number ("The spectators came in large numbers"); to the successive editions of a periodical publication ("The next issue of the journal will have 150 pages"); and to the parts or acts of a show ("The number of the clown was the most fun").
It is also known as a lottery ticket number or a raffle: "If my number is drawn, I buy a new car."
Integer numbers.
Numbers are signs or sets of signs that allow you to express a quantity in relation to your unit. The concept comes from the Latin numĕrus and allows various classifications that give rise to sets such as natural numbers (1, 2, 3, 4 ...), rational numbers and others.
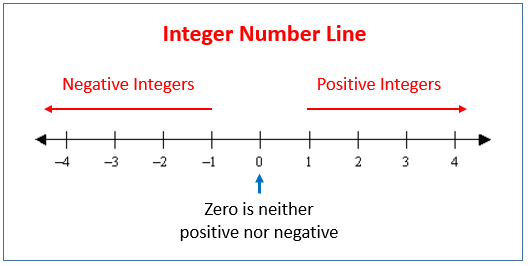
Integers include natural numbers (those used to count the elements of a set), including zero and negative numbers (which are the result of subtracting a larger natural number from a natural number). Therefore, integers are those that do not have a decimal part (ie, 3.28, for example, is not a whole number).
Source
In addition to the above, we can not ignore the fact that whole numbers also serve to establish the height of a monument or a natural element. Thus, for example, we can say that the Mulhacén is the highest peak that exists in the Iberian Peninsula because it is located at 3,478 meters above sea level, while the Teide is the highest in Spain when it reaches 3,718 meters.
Negative integers have various practical applications. With them, you can point to a temperature below zero ("At this time, the temperature in Bariloche is -10º") or a depth below sea level ("The sunken ship was found at -135 meters").
It is important to keep in mind that whole numbers are the result of the most basic operations (addition and subtraction), so their use dates back to antiquity. The Hindu mathematicians of the sixth century already postulated the existence of negative numbers.
In the same way, we can not ignore the fact that we can also carry out multiplication tasks with the so-called whole numbers. In this case, it is important to underline that there is a need to determine, on the one hand, what are the signs of the numbers that participate in the operation and, on the other hand, the product of the absolute values.
Prime numbers
It is known as the prime number to each natural number that can only be divided by 1 and by itself. To cite an example: 3 is a prime number, while 6 is not since 6/2 = 3 and 6/3 = 2.
To refer to the quality of being a cousin, the term primality is used. Since the only possible number is 2, it is usually cited as an odd number one number one priority than this one.
The Goldbach conjecture, proposed by the mathematician Christian Goldbach in 1742, points out that any event greater than two can be expressed as the sum of two prime digits (4 = 2 + 2; 6 = 3 + 3; 8 = 5 + 3 ). Since no mathematician has been able to find an even number greater than 2 that can not be expressed by the sum of two prime numbers, it is believed that the conjecture is true, although it could never be proven.
Source
Primality is very important since it implies that it can be factored into a product of prime numbers. This factorization, on the other hand, will always be unique.
Around 300 BC, the Greek mathematician Euclides had already shown that prime numbers are infinite. There are some rules that allow you to check if a number is prime: for example, any number that ends in 0, 2, 4, 5, 6 or 8, or whose digits add a number divisible by 3, is not a prime. In contrast, numbers that end in 1, 3, 7 or 9 can be primes or not.
Numbers that are not primes (that is, those that have natural divisors besides 1 and himself) are known as compound numbers. By convention, 1 is not defined as a prime nor is it defined as a compound.
The applications of prime numbers are many and are often related to encryption techniques. For example, in the case of the algorithm called RSA, a key is obtained through the multiplication of two prime numbers greater than 10100; since there are no ways to quickly factor such a high number with conventional computers, it is very reliable.
Rational numbers.
In mathematics, the concept of rational numbers is known to refer to those indicators that allow knowing the quotient between two integers. The notion of rational comes from ration (part of a whole). The rational numbers are formed by the integers (which can be expressed as a quotient: 5 = 5/1, 38 = 38/1) and the fractional numbers (the non-integer rational numbers: 2/5, 8/12, 69/253 ).
Each of the whole numbers has another character that follows it; so that the -1 is followed by 0 and the latter by 1, successively, and in turn between each of these there are infinite non-rational numbers.
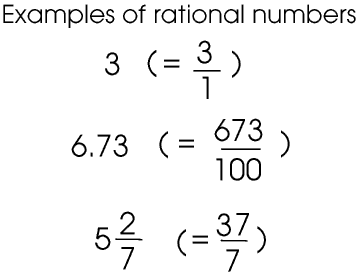
Source
The rational numbers allow expressing measures. When you compare a quantity with your unit, you usually get a fractional result. For example: If I divide a pizza into two parts, I have two halves. Each serving will be 1/2 of the pizza (one part of two). In case of taking both portions, I will have the whole pizza (2/2 = 1).
The rational numbers can be added, subtracted, multiplied or divided (except for zero). The result of these operations will always be another rational number. Since whole numbers can be positive or negative, the Law of Signs applies. The way to specify the operations will vary according to the existence or absence of the same denominator in the fractions.
References.

Congratulations @conceptual-book! You received a personal award!
Click here to view your Board
Congratulations @conceptual-book! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!