You are viewing a single comment's thread from:
RE: Particle in a Double well potential: A molecular dynamics toy example using openMM toolkit
Wow, very nice. But I have to admit I have to read your other publications as well to get further into this subject. Where are these two minima from again? Don't get it!
Regards
Chapper
Hi @chappertron : Thank you for stopping by :) So the minimas are embedded in the potential function which I defined in the beginning.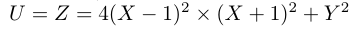
This is how the function is:
You can see that there are 2 minimas at X=1 and X=-1 in this function.
See this plot(@ Y=0):
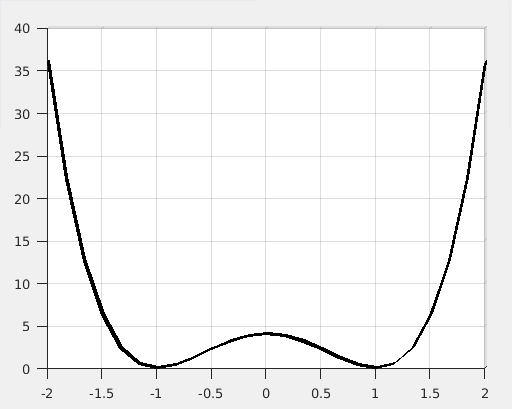
You saw the 2 minimas? Our particle toggles between these 2 states.
Oh of course! I have to look closer next time. Reminds me of my biophysics courses at the University used to.
So this equation would explain why the yellow dot moves as it moves in a crowd of smaller particles?
No. If the yellow particle was allowed to move freely, Potential surface would be like a flat plane surface. But now if I compel my particle under this curvy potential with two minimas, that is what I am defining by this equation. Great question btw. I should have been more clear in the article. But I hope people read comment section too. :)
By the way, just defining this potential function won't make things alive. That's what the langevin equation is there. That equation gives life to the particle under whatever potential you define.
Very cool reply!
The langevin equation makes things become alive
That's mathematics at it's best.
Thanks again
Best
Chapper
Hello dexterdev!
Congratulations! This post has been randomly Resteemed! For a chance to get more of your content resteemed join the Steem Engine Team