Will you win the ski weekend with one of your friends? - Hypergeometric distribution basics
In contrast to the binomial distribution where the probabilities for each outcome were fixed during the whole experiment, hypergeometric distribution describes the case in which the probabilities for a certain outcome change after every observation. The following formula is used to calculate such an event:
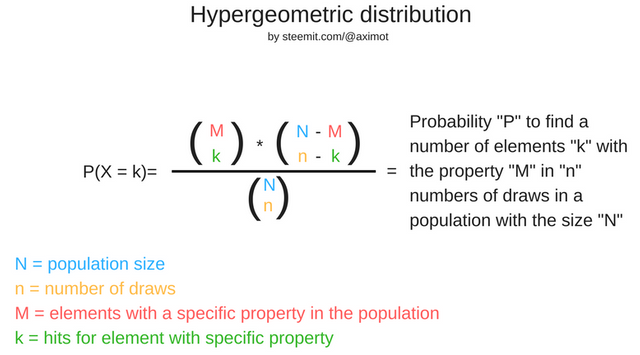
Reminder: The clamps are all binomial coefficients, calculated by n!/ k!*(n-k) where n! is a so called factorial (e.g. n! = 5! = 5*4*3*2*1)
As already said in the introduction, it can be characterised by the aspect that after every draw the probability changes (see example) and that the result can be classified into one of two mutually exclusive categories (dice: 6/no 6, employed/unemployed, red/not red...).
Urn problem
A classical example for this would be the urn problem. This display of the experiment simplifies it if for later models. Imagine you got 12 balls in an urn, 3 red ones, 2 with the color blue and 7 black balls. In total, we got 12 balls, meaning our poplulation size N = 12. If we want to know how probable it is to get 2 red balls by taking out 4 balls after each other, we know our elements with a specific property in the popultaion are M = 3 as we have 3 red balls and we search for k = 2 hits in n = 4 draws. The black and blue balls won't get separated into two different elements, as we search for a specific property, so every other property forms the opposite event ( total red balls = 3/12, "not red" balls = 9/12). These given parameters can simply be put into the given formula.
For the red balls: (N n) = (5 3)
For other colours: (M k) = (5 9)
Possibilities to draw red or another colour are independent:
(N-M n-k )
There are (N n) possibilities to draw n balls without putting them back
Example
Imagine you are at a tombola in a big hall with a stage. You are the first person of 20 that won a 2 days all-inclusive skiing trip at an anniversary of you local skiing club. Unfortunatly, you are new in the club and would feel much better if one of your 4 friends (all at the party too) would come with you. Knowing the hypergeometric distribution, you can now calculate how probable it is for one of your friends to go on the trip with you:
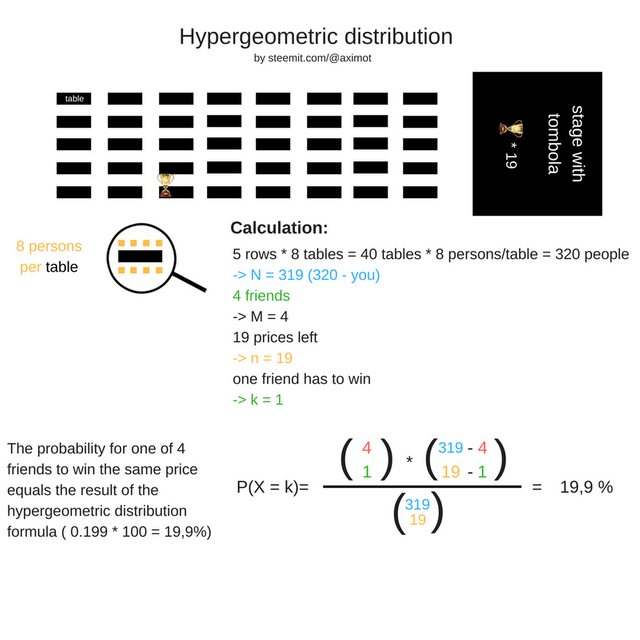
As you can see, there is a roughly 20% chance for one of your friends to join you on the skiing trip, which isn't a small but neither a big chance. For k = 4 ( all your friends can join), the probability is just about 5%. We couldn't have used the binomial distribution here, as every time a person wins, the probability for the next person changes. At the beginning it was 1/320. After you won, there are only 319 possible winners left. If one person could win all the prices, then we could have used a Bernoulli process instead.
Have a nice day :)
SourcesTexthttps://www.frustfrei-lernen.de/mathematik/hypergeometrische-verteilung.html (translated)http://www.poissonverteilung.de/hypergeometrische-verteilung.html (translated)https://en.wikipedia.org/wiki/Hypergeometric_distributionPicturesAll pictures were created with Canva.com
Being A SteemStem Member
This is very interesting, I wrote a post on the usage of hypergeometric distributions today for poker/card games.
I checked your article out. Very good explanation you got a new follower :D
Thanks :D
I have been watching your profile for a little bit
Congratulations @aximot! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP@steemitboard, As I have said repeatedly, I also remain 100 percent confident in Special Counsel Robert Mueller. The contents of t… https://t.co/qObXI0DtQm