How much water fits into this solid of revolution? - The disc method
Today I want use integration to calculate the volume of a simple glass bowl:
Disk method
The concept is similar to the normal integration to calculate the area under a function. I use two functions, the first one is f(x)= 1,5*√ (x-0,5) and the second one e(x)= 0,5x+1. These two functions rotate parallel around the x-axis, forming a 3-dimensional body, a so-called solid of revolution. To make it more realistic, two bounds for each function were added. The total height and maximal width is marked red below:
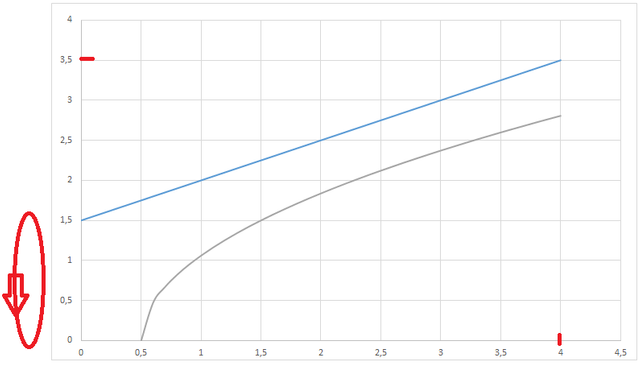
the blue graph belongs to e(x) and the grey one to f(x)
As you can already see, there is a gap between the two functions. This is the glass which is used to built the bowl. If we want to know the volume of the bowl now, we have to use these equations:
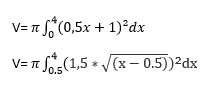
Both integrals get squared and multiplied with the factor π. If we want to know where these factors come from, we just imagine the same as the approach with the normal integral by using areas under the function to approach to the area:
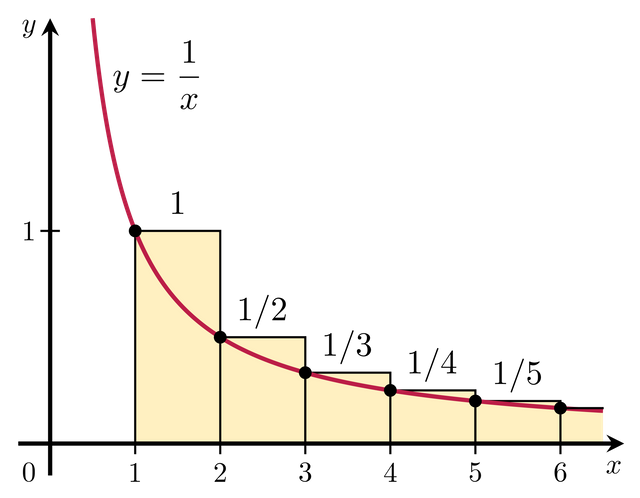
In this case, we have a 3D body and therefore the rectangles are now discs with the radius r.

Imagine you would divide this cylinder into 4 pieces. Each of these discs got a radius r, which is equal to the value of g(x) at its position. For an area of a circle, the formula is 3,1415*r² and we try to use an infinite amount of discs to approach to the integral to be as precise as we can.
Volume of the solid & glass
If we use our glass bowl, the result is about 42,4cm³:
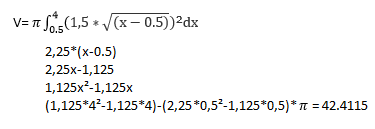
We can put in about 42 mililitres an have to use 54,45426 - 42,2115 = 12.24277 cm³ of glass to build the bowl:
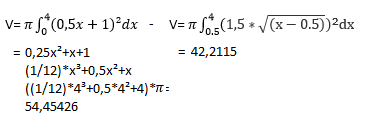
Maybe not as fancy as this one:

,but still a cool method to create a solid a definetly something very interesting if you are able to create even better three-dimensional constructs.
Thanks for reading :)
SourcesTextErnst Klett Verlag, Lambacher Schweizer Seite 116 ( 1.Auflage) (translated) https://en.wikipedia.org/wiki/Solid_of_revolutionhttps://www.cliffsnotes.com/study-guides/calculus/calculus/applications-of-the-definite-integral/volumes-of-solids-of-revolutionPictureshttps://upload.wikimedia.org/wikipedia/commons/thumb/6/67/Integral_Test.svg/2000px-Integral_Test.svg.pnghttps://upload.wikimedia.org/wikipedia/commons/thumb/0/0b/Surface_of_revolution_-_cylinder.svg/1024px-Surface_of_revolution_-_cylinder.svg.pnghttps://cdn.pixabay.com/photo/2014/09/01/14/48/glass-bowl-432875_960_720.jpgAll other pictures were created with Paint.net