Differentiation basics pt.1 - The differential quotient and the derivative rules
The derivative of a function f at the point x equals the slope of the graph of the function f in this point and is mostly declared with f'(x). To calculate the slope of the function's graph, we use the differential quotient, explained in the following:
The differential quotient
Taking two points of which the first point in this example is (2 / f(2)) and the second ( x + h / f(x+h)), we can construct a secant "g" between the two points. As the derivative describes the slope at a single point, the idea is to reduce the distance "h" between the two points until it is minimal: h -> 0. Our secant g transforms into a tangent now which equals the slope at the point (2 / f(2)).
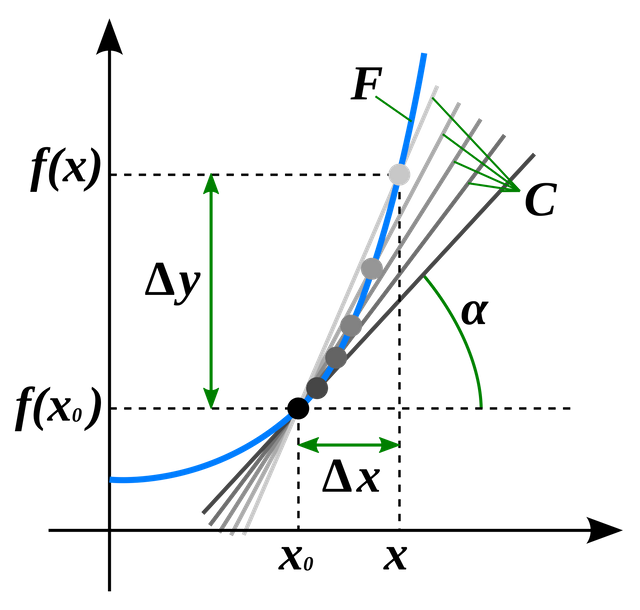
The grey points try to show the reduction of the distance between x0 and x. In terms of calculating this shifting from x into the direction of x0, the method below works:
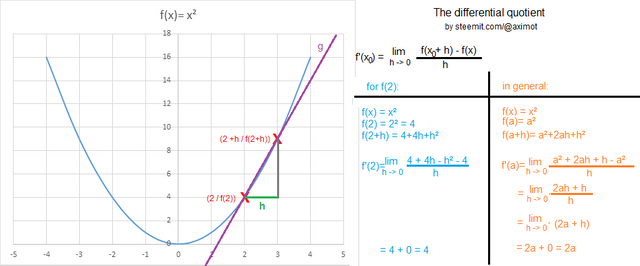
The tabel shows how to form the differential quotient for the function x² for a specific value (x=2) on the left and on the right the calculation in general. It's formula can be simply explained with a gradient triangle: height difference/length difference = f(x0 + h) - f(x)/h. In the picture on the left side, the height difference is shown by the grey line, length difference through the green line. Moving h -> 0 can be graphically describe by moving point (2 + h/f(2+h)) closer to the stationary point (2/f(2)) until no distance is left between them: h -> 0.
Using these information, a simple definition for the first derivative can be formed:
The derivative of a function f at a certain point x0, equals the slope of the tangent which touches function f at P (x0/y0) and therefore equals the slope of the function f at the Point P too.
If you would analyse the results of the differential quotient for different values, rules can be formed:
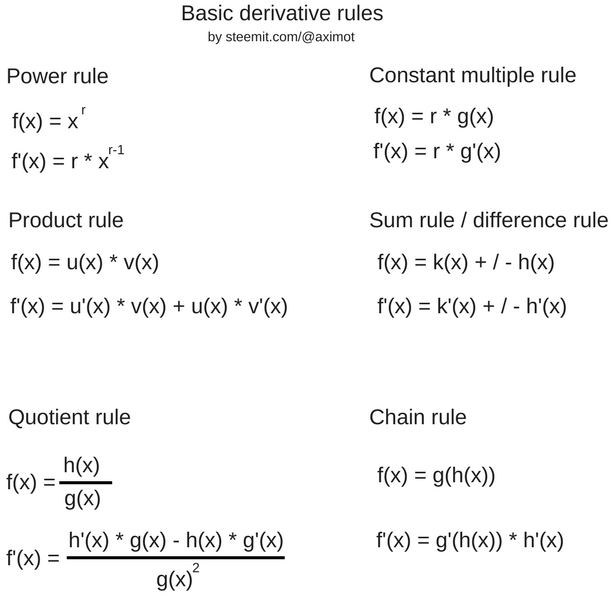
Instead of forming the differential quotient every time to calculate the derivation of a function, we can apply these rules to calculate it much faster. The rules can be simply proven right: Take as much different functions of the type n*x^b, the result will always correspond with the rule x^r -> r*x^r-1.
Some examples:
Power rule:
f(x)= x^7
f'(x)= 7x^6
Constant multiple rule:
f(x)= 4x^3
f'(x)= 4 * ( 3x^(3-1)) = 4*3x^2 = 12x^2
Chain rule:
f(x)= (x²+3)^3
f'(x)= 3*(x²+3) * 2x
As these rules can be relatively simply used, some cases occur which are a bit harder to solve:
Problem 1: Radicals
Every radical can also be written as an exponent:
f(x)= √ (x) = x^(1/2) -> Product rule: f'(x)= 0,5x^-(1/2)
The denominator of the fraction in the exponent depends on the kind of the radical:
f(x)= 4√ (x)= x^(1/4)
The numerator on the other hand depends on the exponent of x:
f(x)= 3√(x^5)= x^(5/3)
Problem 2: Fractions
Not for every fraction the quotient rule is necessary:
f(x)= 1/x -> f'(x)= -(1/x²)
If you don't want to use fractions, an easy way is to rewrite the fraction into a variable with a negative exponent:
f(x)= 1/x -> x^-1
Derivate a negative exponent, the power rule is still applying, so the exponent will even get more negative:
f'(x)= -x^-2
Turning the situation around, x is the numerator now:
f(x)= x/2
If we want to keep it as simple as possible, rewriting can help:
x/2 = (1/2)*x
f'(x)= 1/2
The same counts for functions where x has got a fraction as an exponent:
f(x)= x^4/16
first we can reduce the fraction -> 4/16= 1/4
Power rule:
1/4 - 1 = -(3/4)
f'(x)= (1/4)x^(-3/4)
Conclusion
This was just a short overview about the derivative basics. The next post will deal with the applications of the derivative and will take a closer look on way more difficult functions, including the constant e, logarithms and periodic functions.
SourcePictureshttps://upload.wikimedia.org/wikipedia/commons/thumb/e/ee/Derivative_of_a_function.svg/2000px-Derivative_of_a_function.svg.pngPicture 2 was created with Paint.NET & Microsoft ExcelPicture 3 was created with Canva.comTexthttps://en.wikipedia.org/wiki/Differential_of_a_functionhttp://www.mathe-seite.de/oberstufe/analysis-funktionsanalyse-grundlagen/ableitung/wurzel-ableiten-brueche-ableiten/rechenbeispiel1/ (translated)https://www.formelsammlung-mathe.de/ableitungen.html (translated)https://de.serlo.org/mathe/funktionen/ableitung-funktionen/ableitung-allgemein/ableitung (translated)https://123mathe.de/differentialquotient-und-ableitung (translated)