Binomialkoeffizient: Die Formel an einem kurzem Beispiel betrachtet
In der Kombinatorik wird häufig der sogenannte Binomialkoeffizient verwendet. Meistens geschieht das, in Kombination mit der Binomialverteilung (siehe vorherige Posts). Er gibt Auskunft darüber, auf wie viele Arten man k Objekte aus einer Menge von n verschiedenen Objekten auswählen kann. Ein einfaches Beispiel wäre die Zusammenstellung zweier Fußballteams aus 22 Spielern.
Man hat nun k=22 Objekte/Spieler und kann diese auf n verschiedene Art und Weisen einteilen. Stellt man sie in einer Reihe auf, kann man diese in der Mitte teilen. Oder aber man zählt durch, wobei jeder mit der Nummer 2 in ein Team und mit Nummer 1 in ein Team kommen. Hier auszuprobieren, wie viele Möglichkeiten es gibt ein Team zu erhalten, wäre extrem umständlich. Glücklicherweise gibt es in vielen Taschenrechnern hierfür den Befehl nCr ("n choose r"), der uns diese Anzahl per Knopfdruck liefert. Damit berechnet man "n über k".
Die Formel um das ganze rechnerisch ohne Taschenrechner zu lösen, lautet:
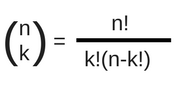
Wenn hinter einem Buchstaben wie hier ein ! steht, bedeutet das "Fakultät" und ist das Produkt dieser und aller kleineren natürlichen Zahlen bis größer 0. Am Beispiel einer Zahl bei n=3: n!= 3*2*1= 6, bzw. bei n=4: n!=4*3*2*1=24.
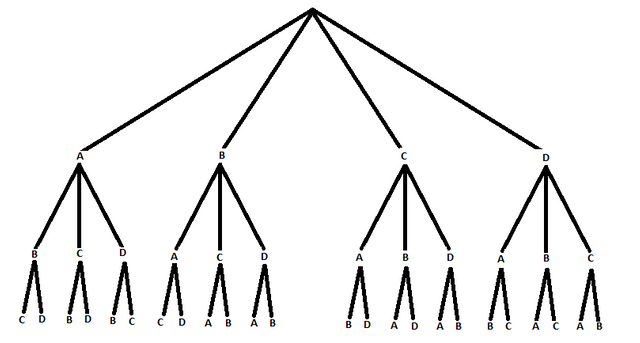
Nehmen wir dieses etwas wackelig gezeichnete, aber trotzdem verwertbare Baumdiagramm. Unter der vereinfachten Annahme, dass wir drei Spieler pro Team per Losverfahren auswählen wollen, gibt es mehrere Möglichkeiten, wie die Lose gezogen werden können. Dabei sind die Buchstaben A,B,C,D jeweils unterschiedliche Spieler.
Es kann Spieler "A" direkt beim ersten Los gezogen werden, oder erst nach dem zweiten oder dritten mal oder sogar gar nicht. Schaut man sich die Pfade genauer an, sind am Anfang 4 Möglichkeiten mit gleicher Wahrscheinlichkeit vorhanden. Da nach einer Losung ein Spieler fehlt, sind es jetzt nur noch 3 und beim letzen Durchgang noch 2. Startet man mit 4 Spielern, bleibt also einer übrig, der nicht in das Team gelost wird. Diese Auswahl entspricht genau den Pfaden im Baumdiagramm.
Man erkennt:
Anzahl der Pfade= 4*3*2= 24
, da die Auswahl an Spielern nach jedem Durchgang um eine Person abnimmt, die in das Team gelost wurde. Pro Losung gibt es eine Auswahlmöglichkeit weniger. Die 24 Pfade kann man am Baumdiagramm ablesen (Pfade sind hierbei von ganz oben bis ganz unten zu lesen).
Dabei ist aber die Reihenfolge noch nicht berücksichtigt. Schließlich kann die Folge ABC auch durch ACB oder BCA... ersetzt werden, da beide das selbe Team hervorbringen.
Dies berechnet man durch die Fakultät:
Bei 3 Personen im Team, können jeweils 3 als erstes gezogen werden. Danach sind es zwei Möglichkeiten und am Ende ist keine Kombinationsmöglichkeit mehr übrig, da die Position der letzen Perosn nun nur noch von einer einzigen Person der drei belegt werden kann.
Somit sind es 3*2*1 Möglichkeiten, oder auch
3!=3*2*1=6
Beweis:
ABC, ACB, BCA, BAC, CAB, CBA sind alle erdenklichen Kombinationen für die drei Personen.
Beispiel an der Gruppe ABC:
Anfangs kann noch jeder der drei Spieler stehen. Sobald nun aber A gewählt wurde, bleiben noch zwei für Position zwei übrig, nämlich B und C. Wird einer der beiden gelost, ist schon festgelegt wer Position 3 einnimmt, da nur noch ein Spieler vorhanden ist.
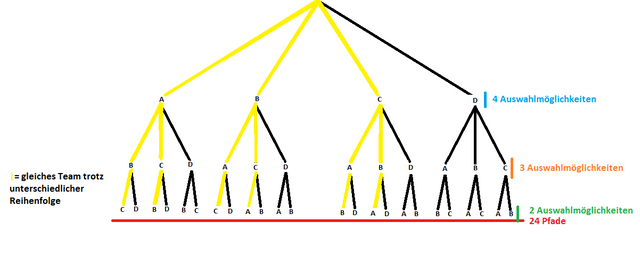
Diese Kombinationsmöglichkeiten für das gleiche Team teilt man jetzt durch die Anzahl an Pfaden, da für den Binomialkoeffizient die Reihenfolge wie man die k Objekte aus der Menge n zieht, nicht berücksichtigt wird. Mit ihm werden nur Teilmengen/Untermengen berechnet und für diese ist die Reihenfolge unbedeutend:
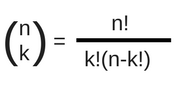
Genau dies macht der obige Term. Nimmt man 4 über 3, "zieht" man drei Lose. Oben steht 4*3*2*1= 24, geteilt durch (n-k!) dies entspricht der Anzahl an Pfaden. Geteilt durch k!, da somit durch die möglichen Kombinationsmöglichkeiten einer Menge geteilt wird. Damit erhält man die Anzahl an Möglichkeiten k Objekte aus einer Menge n zu zu ziehen.
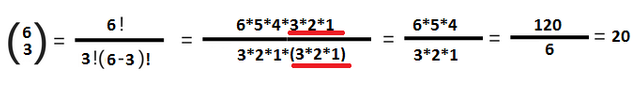
Das rot unterstrichene Produkt kürzt sich dabei sinnvollerweise raus, da auch nur 3 Pfade verfolgt werden und nicht 6. Im obigen Beispiel wird dies theoretisch nicht benötigt, da bei 4 über 3 nur die 1 gekürzt wird, was auf das Ergebnis keinen Einfluss hat. Betrachtet man diese relativ einfache Formel auch unter dem Aspekt der Herkunft des Bruches, versteht man nicht nur wann, sondern auch wieso man diese Formel anwendet.
Das ganze dient als Grundlage für den binomischen Lehrsatz zum dem demnächst ein Post folgt.
Danke für's Lesen :)
QuellenTexthttps://de.wikipedia.org/wiki/Binomialkoeffizienthttps://www.youtube.com/watch?v=TeOzV6DZhW4&t=42shttps://matheguru.com/stochastik/binomialkoeffizient.html Bilder Wurden selbst mit Paint erstellt und auf meinem Imgur Account veröffentlicht