The mathematical language of Ants inspires scientists for artificial intelligence

Earlier many scientists put experiments, which convincingly showed that ants can count within the first dozen. They also have access to the simplest arithmetic operations - addition and subtraction, and they actively use these skills when searching for food. As it turned out, ants are not only familiar with the beginnings of arithmetic, but to transmit counting information they are able to invent new codes that are convenient for specific cases. The results show that the ant language is not a frozen conglomerate of instinctive signals; it changes according to the current tasks, like other effective means of communication in groups. Such uneasy information needs can be provided not only by the developed brain of higher animals, but also by the nervous ganglia of insects. Thus, the line between "higher" and "lower" forms of thinking is gradually eroding.

Anthill is a community of individuals, the well-organized organization of which requires, in one way or another, to transmit to each other various useful information; in particular, ants transmit and receive information about the number and number of objects.
It is believed that a person is smarter than all other animals. Carl Linnaeus, who gave the name to our species, reflected this in his Latin name - Homo sapiens. Our contemporaries, prone to analysis, try to evaluate every property quantitatively. Including the mind. For this, various tests have been invented, in particular the widely used IQ test - Intelligence Quotient. The higher this figure, the smarter the individual. But the trouble is that this test is invented by people and for people, it evaluates the properties of the mind that are important to people, and the means that are accessible to human perception. But imagine for a second that you would have to take an IQ test, compiled by a dove and suggested to you by a pigeon scientist. There is no certainty that you would advance further in this test beyond the initial positions.
Clever Parrot__source
Pigeons and bees have an amazing ability to classify, and they have a highly developed spatial representation of the object. Apparently, these properties among other, equally useful pigeons, and will form the basis of the pigeon test for reasonableness. If someone needs a visual proof of bird's mental superiority, then you can watch a video with an intelligent parrots solving puzzles. The parrot copes with the task much more effectively than the brave ones who accepted the challenge of the parrot, and one of the competing boys, who is probably smarter than the other rivals, even tries to spy on the parrot the way to solve the puzzle: if the parrot can not be defeated, then at least solve the problem.
Returning to the best tests on IQ, it must be emphasized that a person in many categories of intelligence loses by one or another animal. Rats, bears and jays have remarkable abilities to orient and memorize objects on the terrain, in this person they do not compete with them. So rat IQ would include running through the labyrinths, where the test person would get confused in the first two corridors, and the rats would easily run to the end. Jay experimenters would force the participants of their experiments to remember where hundreds of treasures are hidden, and the stupidity of people who remembered the location of only a dozen would be amazed. A chimpanzee test for IQ, or even suggested by paper wasps, could include the ability to recognize and memorize a myriad of comrades in person and / or other attributes: and again, a person would be among the last of the twins.
So, investigating the mind of animals, it is always necessary to take into account that many of them developed other fragments that are necessary for the survival of this particular species in the specific conditions of its habitat.
In addition, the study of certain aspects of the mental activity of animals is further complicated by the "difficulties of translation". The animals passing the tests must first understand what the experimenter wants from them, then solve the experimental problem, and then also express their decision to the means preferred by the experimenter. The experimenter for some reason does not require from himself the understanding and acceptance of the natural symbolism for the animal under test. Meanwhile, the work in the codes proposed by the experimenter requires additional mental effort and understanding skills from the experimental animals (try to participate in the mathematics lesson at the Chinese school, even with the first-graders, and two for the lesson is guaranteed).
It is not known who people are testing - the average representative of the experimental class or individual genius-translators, who can adequately understand and respond to the proposed task. Experimenters Zhanna Reznikova from the Novosibirsk Institute of Systematics and Ecology of Animals and Boris Ryabko from the Siberian State University of Telecommunications and Informatics proposed a technique for studying the formic intelligence, in which ants were not required to master signals and codes invented by people.
They used the ant system of information transfer in experiments, and the success of the test tasks was judged by the final result. At the same time, they studied not just the presence or absence of reason in ants (on this subject let philosophers and theologians reflect), but the ability of ants to arithmetic account. Yes, yes, we checked the ability to arithmetic not even for higher monkeys, but for ants, which, like the rest of insects, do not have a brain as such.
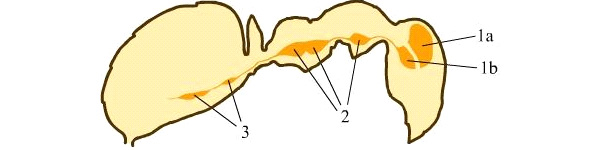
The central nervous system of the ant is composed of the superfluous nerve ganglion (1a), the subpharyngeal nerve ganglion (1b), the thoracic nerve ganglia (2), and the ventral nerve chain (3).
As is known, the central nervous system of an ant consists of several nervous ganglia and the abdominal neural chain. The supra-orbital nerve ganglion, the largest of them, performs the function of the cortex of the cerebral hemispheres in higher animals; there are formed conditioned reflexes. It would seem that the intelligence of an ant with its superhumoric ganglion can not be compared with the mind of a person possessing a giant brain with a developed cortex of the cerebral hemispheres (the relative volume of the "brain" of the ant Formica 1: 280, human - 1:41). It is all the more strange to suspect that the ant has knowledge in the field of mathematics, this music of the spheres. Nevertheless, Novosibirsk scientists have encroached on the "music of the spheres".
The fact is that mathematical skills are decomposed into a number of simpler components, for example comparison of objects by quantitative characteristics, an abstract estimate of quantities and their recalculation. Arithmetic itself or counting is not only the performance of arithmetic operations, but also some elementary operations: the comparison of elements with each other in the rows of objects, the comparison of the number of different quality objects, the preservation of the order of objects - first first, second, third, etc. Such an elementary account is used by many animals.

In an experiments , a chimpanzee sees an Arabic numeral on the screen and selects the appropriate number of points.
Macaque rhesus recreates the number and order of appearance of objects within the first ten, pigeons and rats can order up to four objects, bees demonstrate the ability to count to four. In experiments with bees, experimenters placed feeding troughs with a syrup between the third and fourth landmarks (these were yellow tents). Landmarks were rearranged from place to place, but the bee still found the third and fourth tent. If the distance between the tents was shortened, the bee, remembering not only about the account, but also about the distance, flew for the fourth tent, stopped and flew back. If, however, the distance between the tents was increased, then bewildered by the great distance, the bee did not reach the desired tent, sat down, and then flew farther to the third landmark, where a well-deserved reward waited for it. During the course of the experiment, not only the distance was changed, but also the orientation of the landmarks, only the position of the reward between the third and fourth landmark remained constant. The bees successfully coped with such an abstraction.

The crow successfully recounts the dots in the troughs and selects the desired one
As it turned out, animals can also easily add and subtract small numbers (1 + 1, 2 + 1, 3 - 1), monkeys (rhesus monkeys, capuchins) operate with numbers up to 6, parrots are approximately the same; pigeons can correctly solve the example of subtraction 12 - 6. The ability to such simple numerical manipulations, apparently, is attached to animals and humans from birth. Thus, it has been experimentally proved that five-month-olds can solve problems 1 + 1 and 2 - 1, and this ability develops before their speech skills.
Thus, many animals, including insects, have the ability to count and the simplest mathematical operations. But to assess the real limits of these abilities, in fact, is not easy because of the experimental error described above: the experimenter requires animals not only to understand the problem, but also to communicate with the help of the code proposed by the person. Meanwhile, the development of mathematical skills involves the use of their own code, based on the communicative features of a particular group of social animals. Novosibirsk scientists saved the ants from the need to comprehend human symbols and allowed them to use their own "crossed antenna", that is, their own language.
The experiments consisted of the following. Ants from laboratory anthills (there were two such anthills) were given the opportunity to find a hidden feeder. The laboratory nests were transparent, which allowed to observe all contacts of the scout and foragers, and all the ants were labeled with individual marks. It should be noted that this hidden feeder was the only food source for laboratory ants, so searching for it was a vital task. In the anthill - both in natural conditions and in the laboratory - forager teams are engaged in the search for food. In each team there is one scout, engaged in the search for food sources. Finding food, he hurries to the anthill and sends information to his teammates. After the foragers, they follow the received instructions and return to the anthill loaded with food. And the scout is sent to the next exploratory expedition.
It is clear that for the effective work of the team the scout must explain to his comrades as precisely as possible how to go and what to look for. Ants use their own means to transmit information. In the laboratory anthill, the "explanation" of the route was associated with the need to pass counted information to the comrades, and the matter here was in the cunning arrangement of the feeder.
The feeder looked like a comb with 25-60 evenly spaced teeth, and the food was on one of the teeth.

Syrup on one of the teeth of the "feeder-comb": the foraging team successfully detected the required tooth.
To investigate in turn each of the teeth is long and inefficient, it would be much more logical and faster to transmit information about the number of the desired tooth. So would a man do. And the ants do the same.
Scientists measured the time that the scout was required to convey information about the food found and send his team on the campaign. (While the scout communicated in the nest with foragers, the "feeder-comb" was replaced with a new one, depriving the ants of the opportunity to use a fragrant scent.) It turned out that the farther from the edge of the comb the desired tooth, the more time it takes to transfer information. And this dependence is close to linear: apparently, ants use codes to number the teeth (first, second, third, fifteenth, etc.) or in some other way quantify the distance. In this case, you can change the shape of the comb, set it horizontally or vertically, bend into a circle, but the linear relationship still remains. That's how the antrogloss ganglion works!
But this is not enough. Scientists have complicated the experiment, deciding to test the ability to create new arithmetic codes. It is known that for frequently used concepts (be it mathematics or something else), a person invents a convenient short name, a special symbol. Ants, it turns out, do the same. If you leave food on different tines in the trough-comb, but on one of them much more often than on others, then this ants should remember the ants better than others and invent special convenient codes for it. This, obviously, will shorten the time of information transfer, and foragers will go faster.
The experimenters took turns picking the teeth 7, 14, 10, 20, and the ants repeatedly received information about these "frequent" teeth. Then, after a series of such marches, the ants were again offered a randomly chosen route, that is, the deliberate unevenness of the feeder arrangement was removed. After again, the dependence of the transmission time of information on the target tooth number was constructed. The new dependence was very different from linear, having its own local minima and maxima.
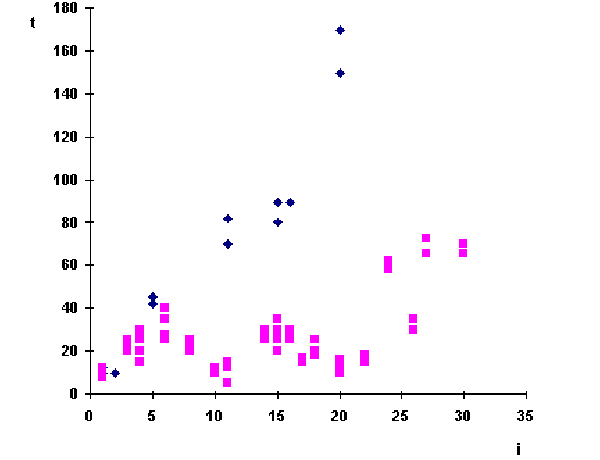
The resulting relationship between the number of the tooth with food (the abscissa axis) and the time spent on transmitting information (the ordinate axis). Blue crosses show the usual experiment, pink squares - after training with unequal, frequent prongs.
Two local minima are located near points 10 and 20, which are often used in ant routes. Scientists have suggested that the reduction in the transmission time of information is associated with the invention of special codes to denote the most frequent prongs. And the general distribution of the transmission time of signals relative to these frequent points suggests that ants use the simplest operations of addition and subtraction. So, to encode point 9, having a special signal for 10, you need to use this short signal 10 and subtract 1. Or number 13 is coded by adding a short signal 10 + 3. Similarly, the Roman account encodes the number XIII (13) as X + III.
Indeed, in the first stage of the experiments, the ants spent about 30 seconds on the designation of point 4, in the third stage they began to spend the same 30 seconds to transmit information about point 14. In all likelihood, the transmitted information would be translated into human language as "go for another 4 points after the turn to the 10th ", that is 10 + 4. Thus, when it becomes convenient, the ants find and actively use new ways of encoding information. Their language, including the mathematical one, is plastic. In ant language, as in any effective communication system, the length of the signal (word, symbol, etc.) depends on the frequency of its use.
This convincing research makes us think not only about the scientific details (the ways of setting up experiments on other animals, the options for interpreting the data obtained and even deciphering the ant language is seen as a particular matter), but about the philosophical questions of the essence of the human mind, the principles of constructing artificial intelligence, the place of mathematics in human thinking and methods of teaching it.

References for Text and Images:
- https://scottlocklin.wordpress.com/2013/07/02/on-the-empire-of-the-ants/
- https://www.pinterest.com/pin/8866530487740930/
- https://www.theguardian.com/science/2014/apr/11/ants-self-organization-quanta
- https://teachbesideme.com/counting-to-100/
- https://theinspiredtreehouse.com/ant-farm/
- https://medium.com/sparrho/ant-inspired-transport-medicine-and-robotics-dd4d1951628e
- http://cronodon.com/BioTech/insect_nervous_systems.html
Support @steemstem and the #steemstem
project - curating and supporting quality STEM
related content on Steemit

A really great post. I used to love ants!
Before my med-school days every time we had a 'pick your own' assignment in any class I'd chose something on ants. Starting from primary school I recon I did a dozen projects and every time I picked a new one i'd learn a whole different side to these amazing creatures. They fly, glide, swim, plan, nurse and (now I've learned) do maths too :)
Thanks @tfcoats for checking the post . It's amazing to watch ants and many other animals , how organised they are. What we learn and see in early age is always memorable and learnable throughout our life. Thanks again for the reply. Good wishes.
You're so right! That being said, got bitten by an ant yesterday and curiosity didn't bring down the sting :'(
good post ... continue good luck
so interesting post!!!
this is real informative post about ants...people are going to believe some important facts about ants
Great article! Also, don't forget the octopuses, they are one of the most intelligent animals :)
Very good picture, I like that, I'm glad to see your post
You have collected your daily Power Up! This post received an upvote worth of 1.53$.

Learn how to Power Up Smart here!