Geometría Descriptiva mediante SketchUp Parte I

Saludos y bienvenidos a todos. Me he dedicado a empezar una nueva serie de publicaciones (además de las referentes a la Estática Aplicada) en las cuales se hace referencia a la Geometría Descriptiva, parte de la geometría que se dedica a describir los objetos del espacio en el plano. Durante el primer semestre en los estudios de Ingeniería o Arquitectura, esta asignatura suele ser para los estudiantes un reto difícil de superar, ya que la comprensión de los procedimientos dados requiere de cierto entendimiento del porqué de los mismos y de la capacidad para imaginar el problema en tres dimensiones. El uso del programa SketchUp para representar los problemas de la Geometría Descriptiva en el espacio y luego representarlos en el plano es de gran ayuda para lograr un mejor entendimiento de los problemas dados.

La comprensión espacial es parte esencial de las habilidades del ingeniero, por ello es parte indispensable de su programa de formación desarrollar la capacidad de abstracción y comprensión espacial. La Geometría Descriptiva cumple este propósito dentro de los planes de estudio de ingeniería en muchas universidades. El Prof. Dr. Ing. Harry Osers expresó en 2010:

”Modernamente se está reemplazando la denominación Geometría Descriptiva por Geometría Constructiva, y que en la enseñanza se le está dando más y más énfasis en la parte formativa de la misma, o sea, a la comprensión y posterior solución de los problemas en el espacio tridimensional en el que vivimos. De hecho prácticamente en ninguna otra asignatura de las que componen el “currículum” del aprendizaje del futuro ingeniero, arquitecto o en general técnico, se enseña el entendimiento del espacio. ”

De esta manera Osers destaca el hecho de que en el caso de asignaturas más avanzadas no se tiende a practicar el entendimiento del espacio, sino que más bien se practica la aplicación de esta habilidad. Esto implica que el estudiante debe de desarrollar de la mejor manera posible el análisis y resolución de problemas geométricos antes de pasar a su aplicación a problemas reales o de mayor complejidad.

Objetivos

La razón de existir de la Geometría Descriptiva es describir los objetos que están en el espacio, los cuales son tridimensionales y se representan sobre una superficie plana (es decir, dos dimensiones), bien sean planos de construcción o la pantalla de una computadora (Osers et al 2012). El Dr. Ing. Harry Osers y sus hijos los ingenieros Miguel, Rodolfo y Tomás se encargaron de plasmar en un libro titulado Estudio de Geometría Descriptiva los conceptos y procedimientos utilizados en esta asignatura.

El objeto de esta serie de publicaciones es aportar contenido didáctico y de calidad que incentive el desenvolvimiento de las habilidades espaciales del futuro ingeniero o arquitecto. Así mismo, a través de futuras publicaciones ilustrar la resolución de problemas prácticos por medio del programa SketchUp, dando así otro punto de vista de los mismos y al mismo tiempo dando a conocer esta herramienta de diseño 3D.

Proyección Ortogonal

La proyección ortogonal es un caso particular de la proyección cilíndrica en la que los rayos de proyección forman un ángulo de 90° con el plano sobre el cual se proyectan (Osers et al 2010). Dicho de otra manera, un objeto en el espacio será representado a través de su proyección ortogonal sobre un plano de proyección, es decir, como si el observador de dicho objeto se encontrara en el infinito, tal como se observa en la Figura N°1.

_{Figura N°1: proyección ortogonal, caso particular de la proyección cilíndrica.}

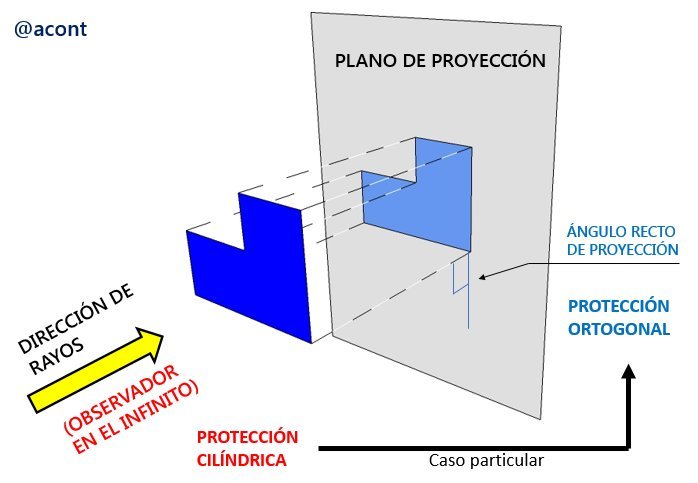
Básicamente, tenemos tres planos de referencia (horizontal, vertical y lateral) los cuales poseen un origen “O” (punto de corte de los tres planos), y la intersección entre los mismos origina los ejes de coordenadas “X”, “Y” y “Z”. Posemos ilustrar lo anterior mediante el ejemplo de un aula de clases, donde cada pared representa cada uno de los planos de referencia (Figura N°2).

_{Figura N°2: el salón de clases puede representar claramente los tres planos de proyección (horizontal, vertical y lateral).}

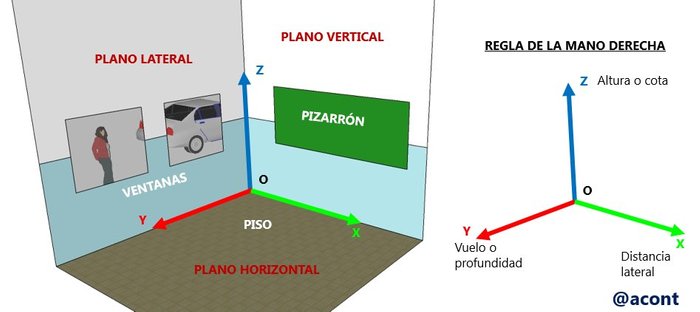
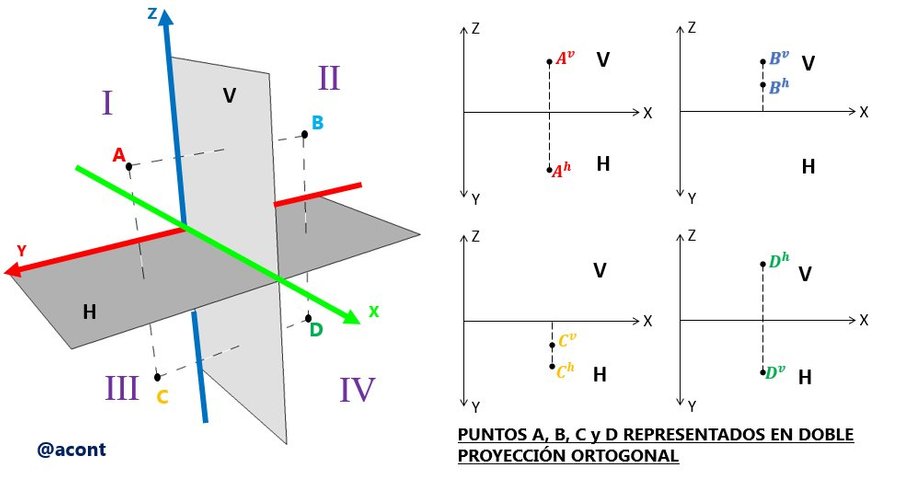
Para la orientación de los ejes utilizaremos la regla de la mano derecha tal como se observa en la Figura N°2. Al establecer tres planos y tres ejes de coordenadas, estamos a la vez generando ocho octantes o zonas dependiendo del signo de cada eje, sin embargo, usualmente solo nos vamos a referir a los cuatro cuadrantes ubicados a lo largo del eje “X” positivo. Estos cuatro cuadrantes se observan en la Figura N°3.

_{Figura N°3: los cuatro cuadrantes a lo largo del eje “X” positivo.}

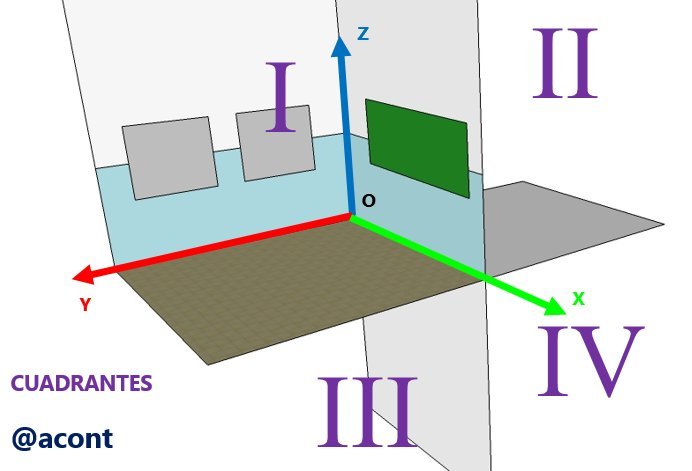
La ubicación de un objeto en alguno de estos cuatro cuadrantes determinará la forma en que el mismo será representado en el plano, puesto que ahora veremos la metodología utilizada para realizar esto: la doble proyección ortogonal. Esta es la esencia de la geometría descriptiva, puesto que es la forma en la que podemos describir un objeto tridimensional en el plano mediante lápiz, papel y los instrumentos de dibujo necesarios.

Doble Proyección Ortogonal

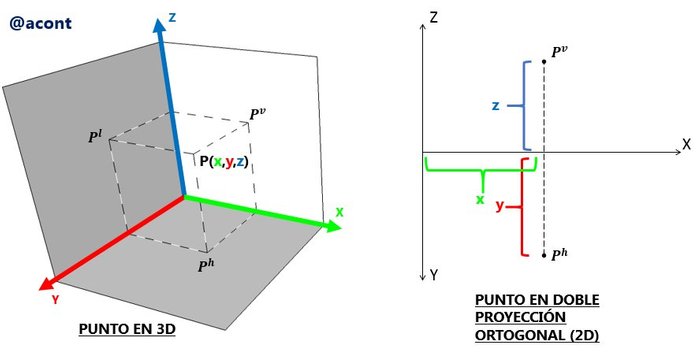
En palabras simples, la doble proyección ortogonal consiste en representar en un mismo plano los planos horizontal y vertical de proyección, dejando al plano lateral como una línea representada por los ejes “Y” y “Z”. El eje “X” es la división entre los planos horizontal y vertical. De esta manera, nos basaremos en la proyecciones horizontal y vertical para ubicar un objeto en el espacio, la proyección sobre el plano lateral no será utilizada. Por consiguiente, un punto tendrá tres coordenadas: su distancia sobre el eje “X”; su proyección horizontal (distancia sobre el eje “Y”); y su proyección vertical (distancia sobre el eje “Z”). De igual manera, un objeto en el espacio será representado en el plano mediante sus proyecciones horizontal y vertical, y de la posición relativa respecto al eje “X” de cada uno de sus puntos (Figura N°4).

_{Figura N°4: objeto en doble proyección ortogonal.}

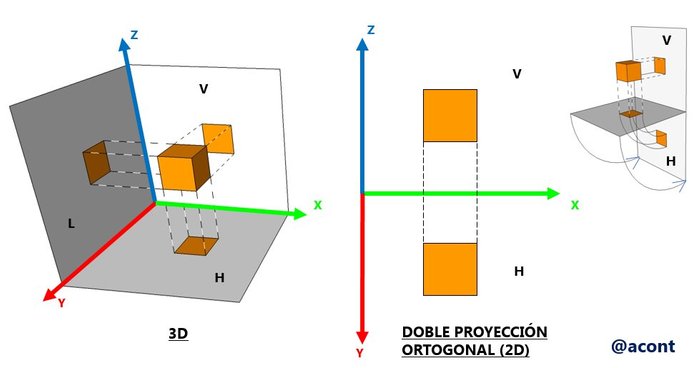
Punto en doble proyección ortogonal

Según lo visto hasta ahora, para representar un punto ubicado en el espacio en el plano, solo necesitaríamos conocer sus coordenadas (X,Y,Z). Sin embargo, para el dibujo utilizaremos una nomenclatura específica, la cual consiste en utilizar letra mayúscula y un superíndice que indica la proyección de dicho punto sobre los planos horizontal y vertical de proyección.

_{Figura N°5: punto en doble proyección ortogonal.}

El signo positivo o negativo de dichas coordenadas indica la posición de un punto en distintos cuadrantes específicos, los cuales se mencionaron anteriormente, y esto repercute sobre la representación de dicho punto en la doble proyección ortogonal. Tenemos diversas posibilidades para la ubicación de un punto de acuerdo al cuadrante donde se ubica (Figura N°6).

_{Figura N°6: la representación de un punto en doble proyección ortogonal varía de acuerdo a su ubicación en cada cuadrante, en el caso del tercer cuadrante las proyecciones horizontal y vertical se invierten al estar en una zona de coordenadas “Y” y “Z” negativas.}

De esta manera se logra representar un punto en doble proyección ortogonal. En el caso de una recta, Osers et al (2012) expresan: “En el espacio la línea recta está definida, bien sea por dos puntos o un punto y una dirección; su proyección pasa por la proyección de este punto”. (p. 29). Por consiguiente, para poder representar una recta en doble proyección ortogonal, necesitaremos como mínimo las proyecciones horizontal y vertical de dos puntos, o en su defecto, las proyecciones en ambos planos de un punto y una dirección dada. De lo contrario, no disponemos de la información suficiente para definir una recta en el espacio y poder representarla en el plano. En la Figura N°7 observamos una recta “a” definida mediante dos puntos. También podemos observar el punto de intersección de dicha recta con los planos horizontal, vertical y lateral y como se representan estos puntos en doble proyección ortogonal. Debemos denotar las rectas mediante letras minúsculas.

_{Figura N°7: recta “a” en el espacio y en doble proyección ortogonal.}

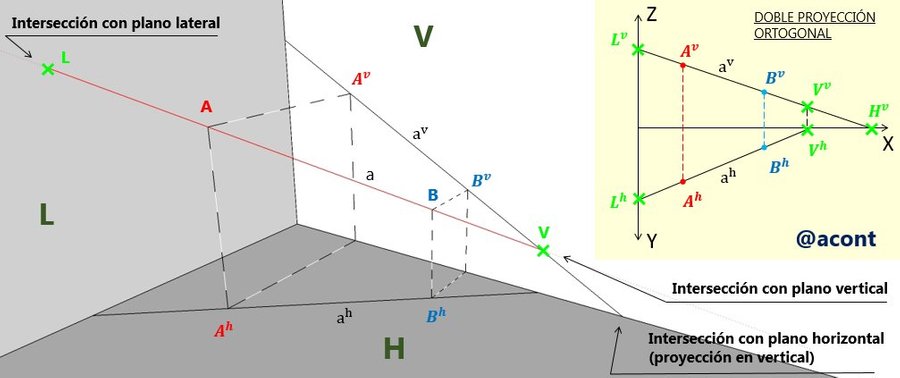
Los puntos H, V y L en la Figura anterior denotan el punto de corte de la recta “a” con los planos de proyección horizontal, vertical y lateral respectivamente. Estos puntos fueron ubicados en la doble proyección ortogonal para una mayor comprensión de la representación en el plano de la recta a la cual se encuentra en el espacio. Se puede observar en la Figura N°7 la ubicación de las proyecciones horizontal y vertical de los puntos L y V en la doble proyección ortogonal, sin embargo, no se conoce la proyección horizontal del punto H.

La pregunta sería entonces ¿Cómo ubicar la proyección horizontal del punto H?

Debemos extender la proyección horizontal de la recta “a” por sobre el eje X, y luego trazamos una línea de referencia vertical que pase por la proyección conocida del punto H. Es importante no olvidar que ambas proyecciones de un punto (horizontal y vertical) siempre deben de estar sobre la misma línea de referencia (perpendicular al eje X), de lo contrario dicho punto posee proyecciones imposibles o carentes de sentido, ya que no coincidirían en el espacio.

_{Figura N°8: recta de la Figura N°7 en doble proyección ortogonal.}

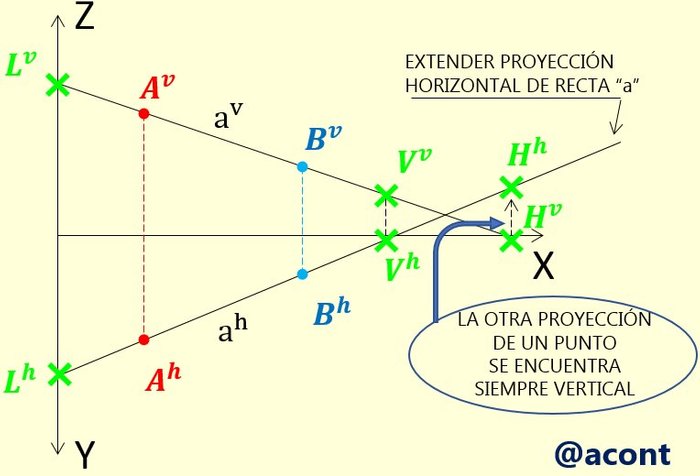
Ahora ¿Por qué la proyección horizontal del punto H se encuentra superior a su proyección vertical si esto no ocurre con los demás puntos?

Si observamos la Figura N°7, encontramos que la recta “a” atraviesa el plano de proyección vertical para luego cortar el plano horizontal antes de pasar por el segundo cuadrante. En la Figura N°3 observamos que en el caso del punto en el segundo cuadrante (punto B), la proyección horizontal se ubica sobre los valores negativos del eje Y por lo que la misma se ubica por encima del eje X en la doble proyección ortogonal. En el caso de la Figura N°7, el punto de corte sobre el eje horizontal tiene cota nula y vuelo negativo (es decir Z=0 y coordenada Y negativa), por ello, en la doble proyección ortogonal la proyección vertical de H se encuentra sobre el eje X y la proyección horizontal por encima de este eje.

En la siguiente publicación abordaremos algunas propiedades de las rectas representadas en doble proyección ortogonal.

Aportes de esta publicación

Contar con material que explique de manera precisa los conceptos básicos de la Geometría Descriptiva a través de ilustraciones que abarquen la situación tanto en tres dimensiones como en el plano para así incentivar el desarrollo de la comprensión espacial, logrando dominar la doble proyección ortogonal de manera más fluida y efectiva.

---

Referencias Bibliográficas

Osers et al (2012). Estudio de Geometría Descriptiva. Editorial Torino. Caracas._Fuente

Material recomendado

Di Pietro, Donato (1985). Geometría Descriptiva. Editorial Alsina. Buenos Aires.

Izquierdo Asensi, F. Geometría Descriptiva. Editorial Paraninfo. Madrid.

---

Imágenes de autoría propia, realizadas mediante el programa SketchUp 8 y posteriormente editadas con Microsoft PowerPoint.

---

Publicado mediante SteemSTEM.io