ESTÁTICA APLICADA: bielas paralelas en sistemas materiales de 1 grado de libertad Parte I
Saludos y bienvenidos queridos lectores de la comunidad científica de Steemit, el día de hoy agregando otro pequeño grano de arena a la cadena de bloques mediante la presente publicación. En esta oportunidad he escrito un poco sobre las “bielas paralelas”, vínculo interno en sistemas materiales el cual puede llegar a agregar un poco de complejidad al análisis de los mismos.
El material completo de Estática Aplicada está recopilado en la siguiente publicación:
En libros y cursos de Estática no suelen estudiarse este tipo de vinculaciones entre cuerpos rígidos (chapas), sin embargo, cuando aparecen suelen ser un dolor de cabeza para los estudiantes. En esta publicación se realiza un análisis puntual y didáctico de las “bielas paralelas” aportando así contenido que ayude a entender mejor esta vinculación poco usual. Durante mi labor como preparador (teacher assistant) de la asignatura Estática Aplicada una de las mayores dificultades de los estudiantes era la de comprender el efecto de dicha vinculación en sistemas materiales, sobre todo al momento de realizar un análisis de la estabilidad o estudiar el comportamiento inestable de un sistema de un grado de libertad. La búsqueda de reacciones externas e internas en sistemas isostáticos sometidos a un sistema de cargas externas también requiere de un análisis específico en el caso de la presencia de bielas paralelas, pero esto formará parte de futuras publicaciones referentes a la Estática Aplicada.
Introducción
Al momento de vincular dos cuerpos rígidos o chapas en el plano, existe la posibilidad de restringir total o parcialmente el movimiento relativo entre ellos. La restricción total de movimiento relativo entre dos chapas se suele llamar empotramiento interno o simplemente junta rígida en donde ambos cuerpos rígidos están vinculados de manera tal que conforman uno solo. Otra vinculación muy común es la rótula o articulación, donde existe la posibilidad de rotación relativa entre miembros tal como puede presentarse por ejemplo, en el cuerpo humano, ya que podemos hacer rotar nuestro brazo respecto al resto del cuerpo (o el brazo respecto del antebrazo) más sin embargo, no podemos hacer que nuestro brazo se desplace manteniendo al resto del cuerpo fijo, o en otras palabras, que nuestro brazo pueda presentar traslación pura sin que el resto del cuerpo también lo haga.
Cuando dos chapas se vinculan de manera tal que solo se permite un desplazamiento relativo entre ellas estamos ante la presencia de una vinculación interna la cual es geométricamente posible pero no muy común en la naturaleza o en sistemas estructurales en el caso de la Ingeniería Civil. Probablemente sea más usual en sistemas mecánicos. Esta vinculación suele llamársele “empotramiento móvil interno” o “bielas paralelas” ya que una representación gráfica de este vínculo interno suele ser un par de bielas paralelas (barras simples) de longitud despreciable articuladas a ambos cuerpos rígidos. En el artículo Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad se da una descripción general de los vínculos en sistemas materiales y del mismo se extrae la siguiente imagen:
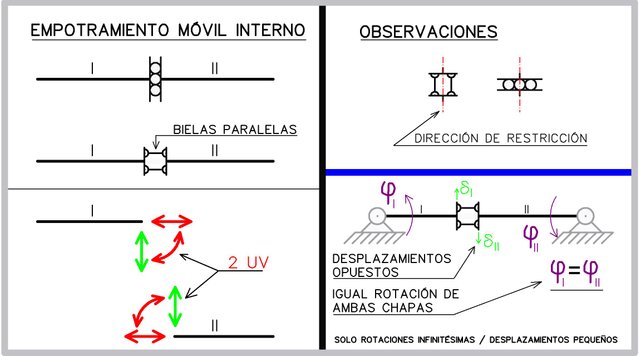
La imagen anterior destaca en rojo las restricciones internas (rotación y un desplazamiento) que existen y en verde el desplazamiento permitido para el caso mostrado donde las bielas paralelas se disponen en dirección horizontal. Se observa también que esta vinculación obliga a ambas chapas a rotar en igual magnitud y sentido.
Polo relativo en el infinito
En el artículo Análisis de Estabilidad de Sistemas Materiales Parte I: teoría y caso práctico se estudió la aplicación del Teorema de Kennedy (Teoremas de los Polos) sobre sistemas materiales para así analizar su estabilidad independientemente de la determinación algebraica de sus grados de libertad mediante una determinada ecuación ya que pueden presentarse vínculos aparentes (vinculaciones que no aportan restricción de movimiento) que introducen más grados de libertad que los que arroja dicha ecuación. Se constató que para el caso de bielas paralelas vinculando dos chapas, el centro instantáneo de rotación (polo relativo) entre ambas se encuentra en el infinito, indicando que no existe rotación relativa entre ellas, sino que ambas deben de rotar en igual magnitud y sentido.
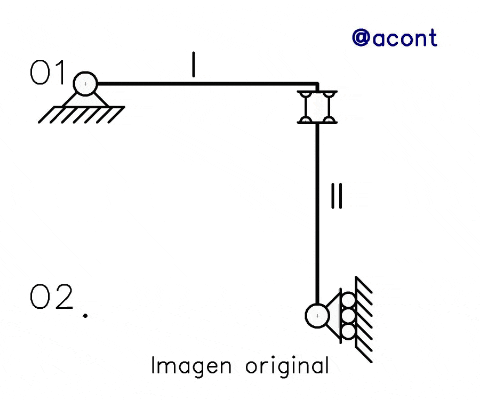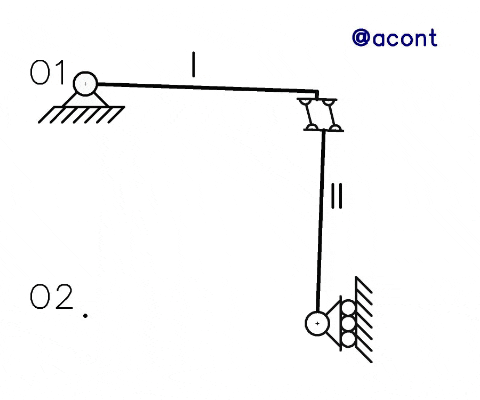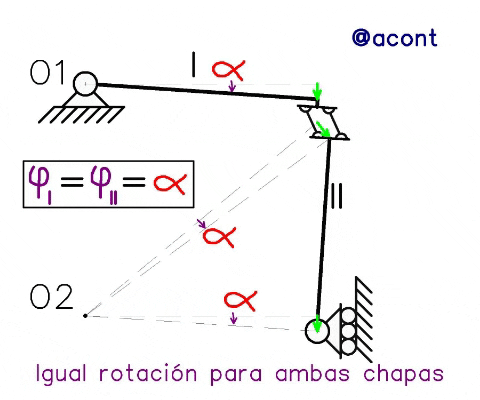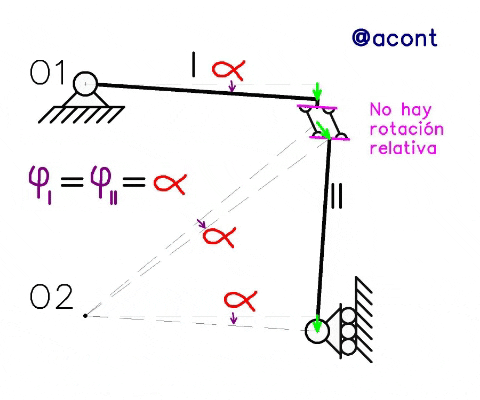
Para analizar el efecto de las bielas paralelas en sistemas materiales vamos a referirnos a la Figura N°1, donde observamos un sistema de dos chapas, la primera articulada a tierra y la segunda está simplemente apoyada mediante un “patín” o apoyo simple, ambas vinculadas mediante bielas paralelas dispuestas de manera vertical. Estudiaremos la estabilidad de este sistema material mediante el Teorema de Kennedy, en específico el primer Teorema de los Polos (1mer TDP). Nos saltaremos el primer paso en el estudio de la estabilidad, el cual consiste en aplicar la ecuación mencionada anteriormente para el cálculo de los grados de libertad.
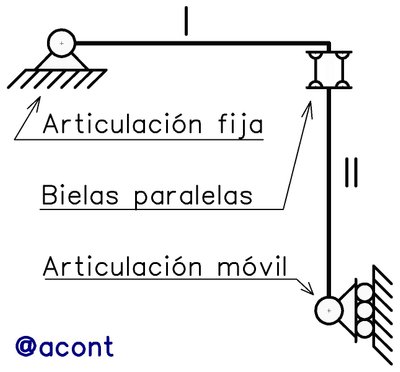
Primeramente, verificamos si es posible hallar un centro instantáneo de rotación (polo) para cada chapa, esto se realiza mediante la aplicación del 1mer TDP, el cual indica que para cadenas cinemáticas de 1 GL el polo absoluto entre dos chapas de un sistema material se alinea con el polo relativo entre ellas:
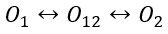
En caso de cumplirse esta expresión, indicando que se alinean los polos absolutos entre sí, se verifica que el sistema mostrado posee 1 GL. Para ello, primero hallaremos los polos de acuerdo a las restricciones de vínculos y luego aplicaremos la dirección dada por el 1mer TDP para hallar los polos restantes que no pudieron hallarse mediante el primer paso. En la Figura N°2 observamos este procedimiento.
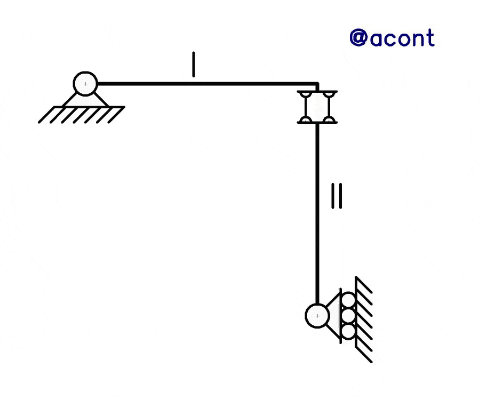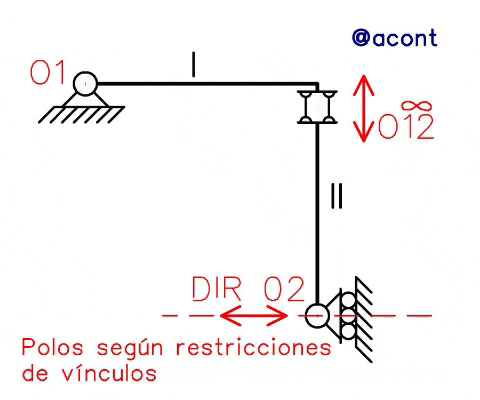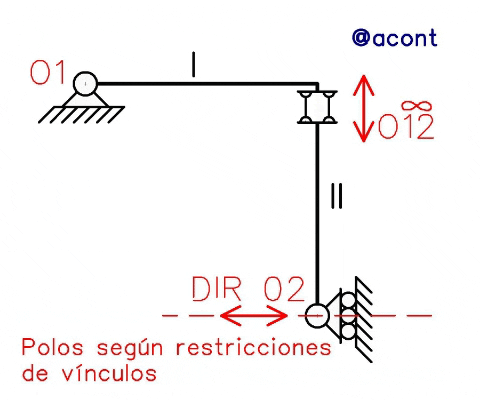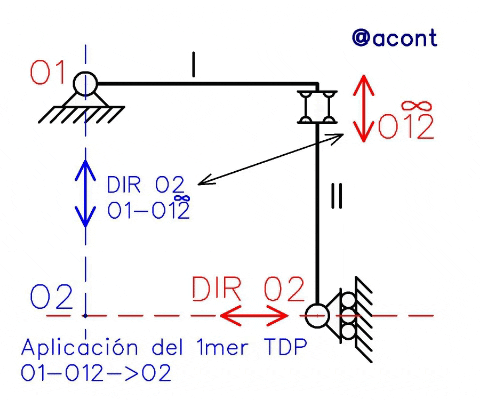
Luego de hallados los polos de acuerdo a las restricciones dadas por vinculaciones (en rojo), se halla el polo restante (de la segunda chapa) mediante el 1mer TDP. Ya que el polo relativo entre las chapas se encuentra en el infinito y no en un punto propio, se traza por el polo absoluto conocido una dirección paralela a la dirección del polo relativo en el infinito (en azul), encontrando mediante intersección la ubicación del polo absoluto de la segunda chapa. Cuando un polo se encuentra en el infinito, no pasa por una dirección específica, sino que esta dirección se replica en todo el plano. Es decir, un error común es trazar una dirección a través de las bielas paralelas, en realidad la dirección trazada debe pasar a través de un polo ubicado en un punto propio (en este caso el polo “O1” ubicado en un punto dado).
Ya que hemos hallado solo 1 polo absoluto por chapa, existiendo alineación de estos con el polo relativo, damos por verificado el cumplimiento del 1mer TDP, por lo que el sistema posee 1 GL.
Conocidos los polos, observamos en la Figura N°3 una animación del comportamiento inestable del sistema material, ya que al poseer 1 GL su movimiento puede ser definido perfectamente, ya que se conoce un centro de rotación fijo y único para cada chapa.
Las bielas paralelas rotan para evitar su deformación, recordemos que estamos suponiendo que todos los elementos son cuerpos rígidos en el plano. Por ello al final de la animación se demuestra la no existencia de rotación relativa entre chapas ya que se mantienen paralelos los segmentos en color rosa, sin alterar así el ángulo de 90° entre cada barra que existe desde el inicio.
Al realizar un análisis bajo movimientos infinitésimos del sistema, encontramos que al asignar a la chapa I una rotación “α” en sentido horario, la chapa II está forzada a rotar en igual magnitud y sentido. También debemos tener en cuenta que el desplazamiento de ambas chapas no será igual en su punto de vinculación debido a la presencia de bielas paralelas. Para entender mejor esto vamos a particularizar las bielas paralelas en dos puntos: “B1” para la chapa I y “B2” para la chapa II respectivamente (Figura N°4).
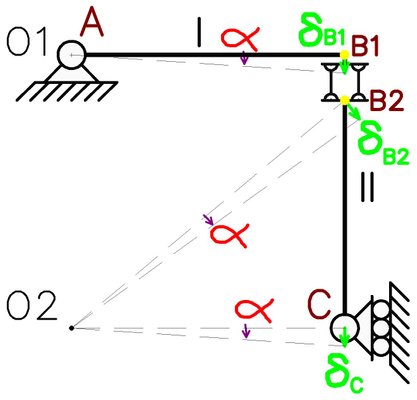
El cálculo de los desplazamientos de cada punto se realiza de igual manera que en el artículo anterior donde se explica el proceso de cálculo de las componentes de desplazamiento de un punto de una chapa sometida a una rotación infinitésima conocido ya el ángulo de rotación de dicha chapa y de las distancias verticales y horizontales del sistema material. Podemos asumir que las bielas son de longitud despreciable y que la distancia entre los puntos “B1” y “B2” tiende a cero, por lo que podemos decir que ambos puntos geométricamente coinciden, pero no presentan el mismo desplazamiento.
De esta manera se refleja el comportamiento inestable de un sistema material de 1 GL que posee bielas paralelas como vinculación interna y se observa que para realizar el análisis por movimiento infinitésimo ante la presencia de bielas paralelas se debe tener en cuenta que ambas chapas vinculadas rotan en igual magnitud y sentido, simplificando así el cálculo de desplazamientos y rotaciones.
Pero puede surgir la pregunta: ¿Por qué el polo relativo se encuentra en el infinito?
Se puede demostrar que el polo relativo está en el infinito asumiendo que cada biela representa una chapa adicional del sistema material, ampliando sus dimensiones desde una longitud despreciable hasta una longitud finita. Podemos realizar esta demostración con un ejemplo sencillo de dos chapas alineadas verticalmente tal como se observa en la Figura N°5. De esta manera obtenemos un sistema equivalente al cual intentaremos hallar el polo relativo entre las chapas I y II, siendo las chapas III y IV ambas bielas respectivamente.

En la Figura N°5, hallar los polos absolutos y relativos entre las chapas que se vinculan en el sistema no representa un desafío, tal como vemos en la Figura N°6:
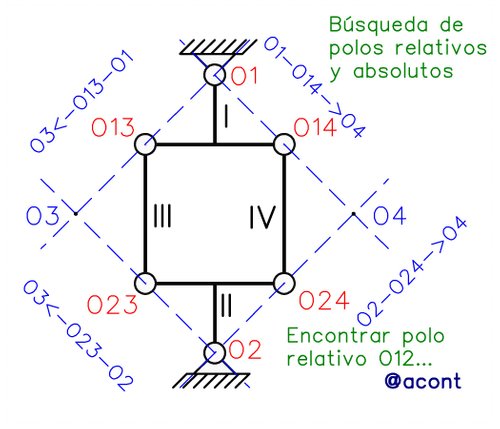
Pero ahora debemos hallar el polo relativo entre dos chapas que no están directamente vinculadas (I y II). Para ello deberemos aplicar el 2do TDP (segundo Teorema de los Polos), el cual dicta que en una cadena cinemática de 1 GL los polos relativos entre tres chapas cualesquiera “i”, “j” y “k” están alineados entre sí [1].
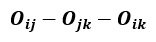

Sabiendo entonces que el polo relativo O12 se encontrará alineado con O13 y O23 (o con O14 y O24), debemos encontrar una dirección adicional la cual nos provee el primer Teorema de los Polos. El 1mer TDP indica que el polo relativo O12 también debe de alinearse con los polos absolutos O1 y O2. Al trazar ambas direcciones sobre el sistema material, el resultado es que las mismas son paralelas, interceptándose en el infinito, ubicación del polo relativo O12 tal como se observa en la Figura N°7.
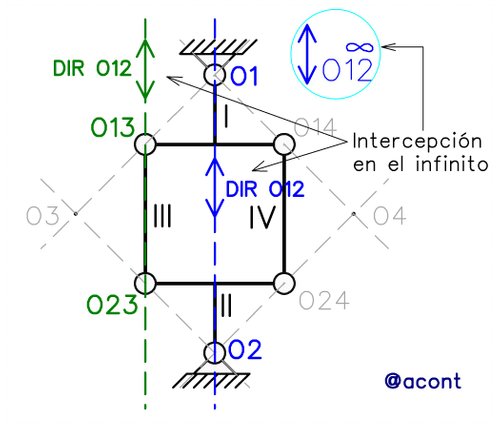
De esta manera se ha demostrado porque en el caso de la vinculación interna denominada “bielas paralelas” el polo relativo se encuentra en el infinito.
Como resultado observamos el cumplimiento del primer Teorema de los Polos entre dos chapas de un sistema material cuando existe esta vinculación interna que solo permite un desplazamiento relativo entre dos miembros o chapas. El 1mer TDP (primer Teorema de los Polos) puede presentarse de varias maneras, y la estudiada en este artículo representa el caso donde el polo relativo se ubica en un punto impropio (está en el infinito), mientras que los polos absolutos se encuentran en un punto propio:
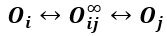
En la próxima publicación se estudiará otro caso de sistema material de 1 GL con bielas paralelas el cual presenta un comportamiento inestable diferente y el 1mer TDP se cumple de manera distinta.
Conclusiones
Referencias Bibliográficas
[1] Rodríguez, Iván. (2003). Estática de las Estructuras. (P. 30) Fuente para consulta
Material recomendado
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word por @acont. Gif creados mediante Giphy.com.
Muy buen artículo, @acont. Seguramente tus estudiantes se benefician bastante de este contenido técnico y tu didáctica. Saludos!
Gracias estimado @eniolw, esta materia como tal tiene pocas referencias y a los estudiantes no les sirve de mucho buscar en internet o ir a la biblioteca de la universidad, por ello busco crear contenido didáctico a partir del poco material disponible. Saludos,
@tipu curate
Upvoted 👌 (Mana: 10/25 - need recharge?)
Gracias!
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.
Congratulations @acont! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPVote for @Steemitboard as a witness to get one more award and increased upvotes!