Análisis de Estabilidad de Sistemas Materiales Parte IV: mecanismo con vínculo aparente

Saludos y bienvenidos! en esta ocasión nos encontramos en la parte IV del tema de análisis de estabilidad de sistemas materiales. En la primera parte se abordaron conceptos teóricos de importancia relacionados al Teorema de Kennedy (o teoremas de los polos) los cuales nos sirven de base para verificar la estabilidad de un sistema material en el plano (condición de suficiencia, dada por la no existencia de mecanismos cinemáticos de 1 grado de libertad) una vez ya verificada la condición de necesidad (vínculos mínimos necesarios para lograr reducir numéricamente a 0 los grados de libertad). En las subsiguientes partes se abordaron casos particulares a través de ejemplos prácticos, tal como es el caso de la presente publicación. Con el objetivo de seguir aportando contenido didáctico a través de las etiquetas #SteemSTEM, #STEM-espanol y #Cervantes, comunidades que apoyan la difusión de contenido académico-científico de calidad en español, a las cuales envío un especial saludo. Sin nada más que agregar, empecemos.

Introducción

Como ya hemos visto en anteriores publicaciones, la estabilidad de un sistema material depende de la cantidad de vinculaciones que este posea, así como también de la geometría del sistema y la manera en que estas vinculaciones están dispuestas. En el caso de mecanismos cinemáticos de 1 grado de libertad, se tiene que haría falta una unidad de vinculación o restricción adicional para que el sistema no pueda presentar movimiento. Estos sistemas poseen una única posibilidad de movimiento para cada uno de los puntos que lo conforman, generando esto que el desplazamiento de cada punto o la rotación de cada chapa pueda ser expresada en función de un parámetro independiente único (un desplazamiento o rotación).

Podemos determinar numéricamente los grados de libertad de un sistema material totalizando el número de unidades de vinculación tanto externas como internas que el sistema posee y el número total de chapas o cuerpos rígidos. Cuando un sistema material que numéricamente posee 1 grado de libertad presenta una vinculación aparente, que no aporta restricción alguna al sistema, resulta fácil deducir que si se elimina esta vinculación se concluye que el sistema no posee 1 grado de libertad sino 2. Esta afirmación no siempre es verdadera y veremos cómo puede darse el caso en el que esto ocurre.

Para lo anteriormente dicho, se analizará un caso en el que se presenta un vínculo aparente en un sistema el cual de por sí ya es inestable.

Análisis de Estabilidad del Sistema Material Propuesto

Para poner en evidencia lo antes descrito, se analizará el siguiente sistema material (Fig. N°1), el cual es el problema N° 2-A de la obra “ESTÁTICA APLICADA” publicada en el año 1998 por el Profesor Suilio Hernández. El mismo será abordado desde un punto de vista más didáctico, mostrando con más detalle la teoría y procedimientos detrás del resultado final.

_{Figura N°1: sistema material a analizar.}

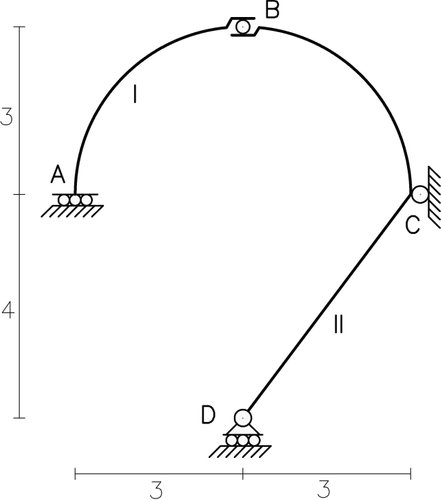
Podemos observar la forma curva de dos de las chapas en lugar de la representación unidimensional acostumbrada, esto es meramente representativo y solo nos indica la geometría del cuerpo rígido. Para efectos del análisis de estabilidad, solo nos interesa la forma en que las vinculaciones están dispuestas y el número de estas. La geometría del sistema puede incidir en la estabilidad, pero no la geometría de cada cuerpo rígido particular.

El vínculo en B se denomina “rodillo interno” y su efecto es el de restringir solo un desplazamiento relativo entre chapas, en este caso el vertical. Tiene el mismo efecto que la biela simple y la articulación móvil interna (“patín interno”). Podemos ver una descripción más detallada de este vínculo en la publicación Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad.

Mediante la Ecuación (3) del artículo Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación podemos determinar los grados de libertad de el sistema material:

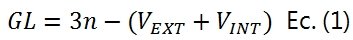
Donde “n” representa el número de chapas, “Vext” y “Vint” la cantidad de unidades de vinculación externas e internas respectivamente.

_{Figura N°2.}

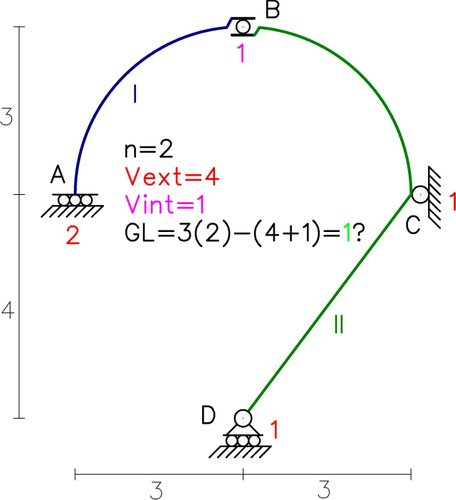
Se ha determinado que el sistema numéricamente posee 1 grado de libertad, por lo que no se ha cumplido la condición de necesidad, es decir, no se dispone del número mínimo de vinculaciones para que el sistema sea estable (grados de libertad igual o menor a cero) concluyendo por ahora que el sistema es inestable y GL= 1. Veamos ahora que se puede concluir con el análisis geométrico del sistema. Para ello se realiza un estudio de posibles polos de acuerdo a la vinculación existente en el sistema material.

_{Figura N°3.}

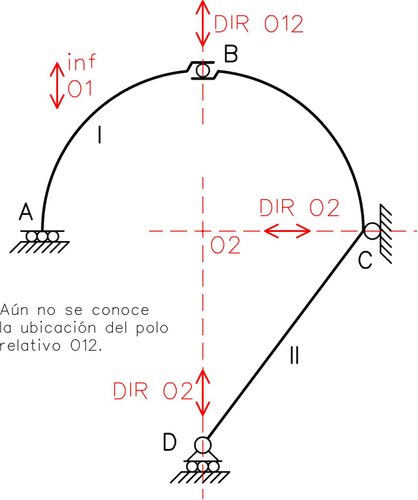
Se observa en la Fig. N°3 que aún desconocemos la ubicación del polo relativo O12 en el sistema, y no se posee información suficiente para establecerla. De esta manera recurrimos al Teorema de Kennedy (específicamente el primer teorema de los polos o 1mer TDP). Para el cumplimiento de este teorema, el polo relativo O12 debe de estar alineado con los polos absolutos ya conocidos de las chapas I y II. De cumplirse este teorema entre las chapas del sistema, se confirma que el mismo posee 1 grado de libertad.

_{Figura N°4: se trazó por el polo absoluto O3 una dirección paralela a la dirección hacia el infinito del polo absoluto O1, para hallar una dirección en la que se encontraría el polo relativo O12.}

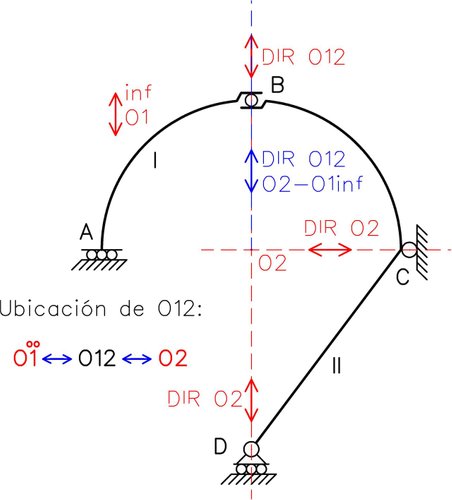
A través de la aplicación del 1mer TDP hemos obtenido una dirección que coincide con la dirección ya establecida por el propio vínculo interno en B (rodillo interno). Aún así, no se posee información suficiente para poder establecer la ubicación de O12, por lo que se encuentra que la ubicación de O12 es indefinida. De esta manera, no se está cumpliendo el 1mer TDP entre las chapas I y II.

Tal como se mencionó en la Parte I de la presente publicación, cuando se tiene un mecanismo de varios grados de libertad (GL>1), aún realizado todos los pasos no se puede hallar el polo absoluto de una o más chapas del sistema (o el polo relativo entre chapas), ya que no se posee la información suficiente para establecer la ubicación del mismo. Esto indica que la ubicación del polo no puede ser definida pues el sistema presenta más de una forma de moverse.

Al no existir una ubicación definida para el polo relativo O12, se dice que el mismo no existe para efecto de movimientos infinitésimos. Si no existe polo relativo, no existe vinculación entre chapa y chapa, por lo que el vínculo interno en B es aparente o “no está haciendo nada”. De esta manera se concluye que las chapas I y II pueden moverse independientemente una de la otra como si no estuviesen vinculadas. Esto convierte al sistema en dos sistemas independientes con 1 grado de libertad cada uno, lo cual no es precisamente, un sistema de 2 grados de libertad.

Hernández S. (1998) señala: “Hablamos de grado de libertad 1+1 y no de GL=2 debido a que cada chapa se mueve de forma independiente”. (p. 37). Teóricamente es incorrecto decir que el sistema posee 2 grados de libertad ya que no existe una vinculación total o parcial entre cada uno de sus elementos, sino que claramente se observan dos sistemas separados e independientes entre sí, por lo que lo correcto es decir que el sistema en su totalidad posee 1+1 grados de libertad.

En el siguiente GIF podemos observar la posibilidad de movimiento de cada sistema independiente, donde existe un parámetro de movimiento independiente para cada sistema (en este caso se asignó un desplazamiento “δ” para la chapa I y una rotación “φ” para la chapa II).

_{Figura N°5. Fuente}

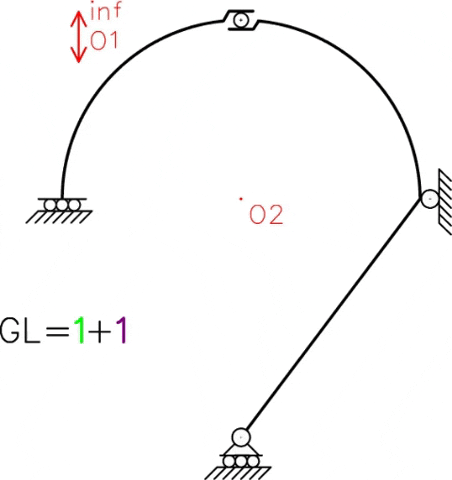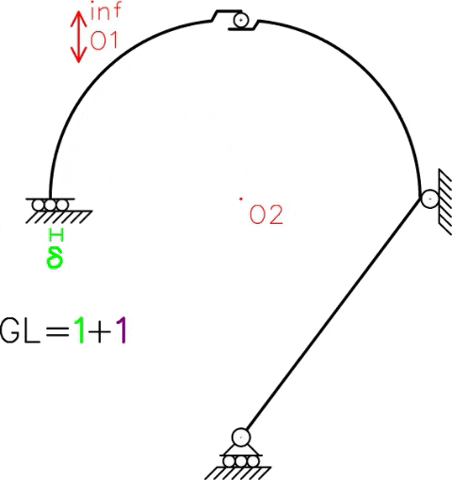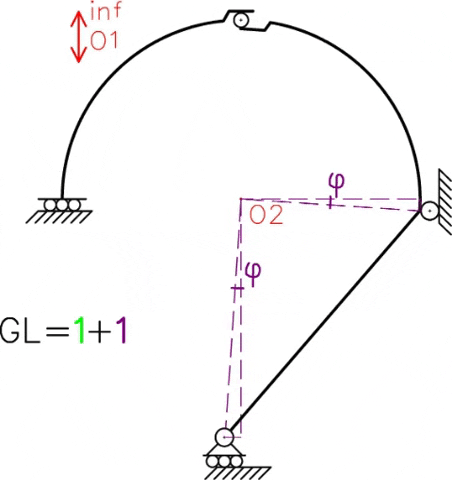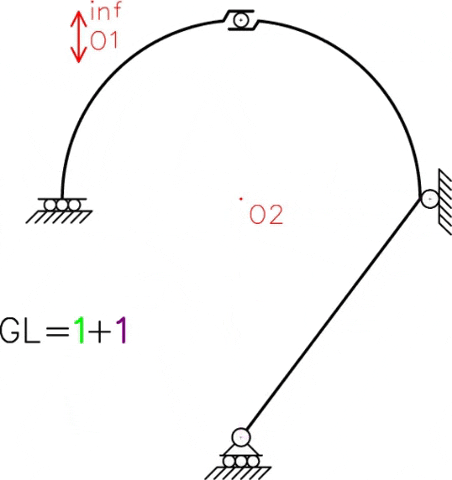
Ahora surge la siguiente pregunta:

¿Qué debería modificarse en el sistema para que la vinculación interna en B no sea aparente?

La respuesta es simple, si anteriormente se llegó a la conclusión de que la vinculación interna B es aparente debido a que la dirección dada por el 1mer TDP coincidía con la dirección dada por el mismo rodillo interno imposibilitando así definir el polo relativo, pues para evitar esta coincidencia se puede realizar lo siguiente: una solución es desplazar horizontalmente la posición del rodillo interno B o del patín en D generando así que ambas direcciones se intercepten en el infinito (existiendo un polo relativo en el infinito o punto impropio); o modificando la dirección de restricción ya sea del mismo rodillo interno o del empotramiento móvil en A generando así un polo relativo en un punto propio. De esta manera se asegura 1 grado de libertad tal como lo indica la Ecuación (1).

---

Como aporte a esta publicación se dejará al lector/estudiante la tarea de analizar la estabilidad del siguiente sistema material (Fig. N°6).

_{Figura N°6.}

---

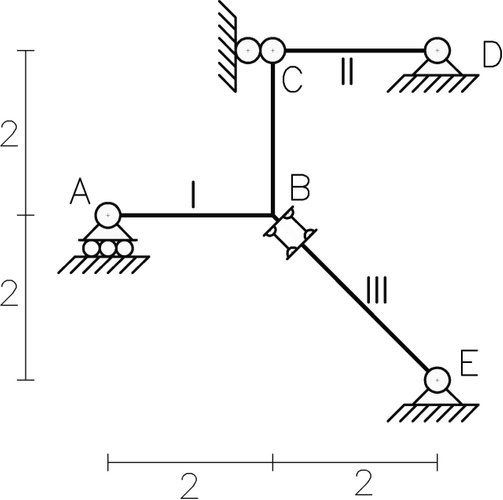
Conclusiones

La geometría interna de cada chapa no incide en la estabilidad de un sistema material, ya que para ello cuentan el número de vinculaciones o restricciones, la manera en que están dispuestas y la geometría del sistema.

No solo los sistemas que cumplen la condición de necesidad pueden presentar vínculos aparentes que los hagan inestables sino que mecanismos o sistemas hipostáticos también pueden presentar vínculos aparentes que los hagan ser aún más inestables.

Al no encontrar la ubicación de un polo aún aplicando el Teorema de Kennedy (o 1mer TDP) no se posee la información suficiente para hallarlo y se dice que la ubicación del mismo es indefinida, imposibilitando el cumplimiento del primer teorema de los polos.

Cuando un vínculo de primera especie (que solo restringe un movimiento) resulta ser aparente, se anula la vinculación entre chapas, generando dos sistemas independientes uno de otro.

Para que la ubicación de un polo desconocido pueda ser definida se debe garantizar que existan dos direcciones que no coincidan, de lo contrario el polo no puede ser definido y el sistema o chapa presentaría más de una forma de moverse.

---

Referencias Bibliográficas

Hernández, Suilio. (1998). Estática Aplicada. Folleto Editado por el Departamento de Ingeniería Estructural U.C.V. Caracas.

Material recomendado

@acont. Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad

@acont. Análisis de Estabilidad de Sistemas Materiales Parte I: teoría y caso práctico

---

Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word por @acont. Gif creado mediante Giphy.com.

---

Publicado mediante SteemSTEM.io